
ЭлМат 1 лаба готовая
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра МНЭ
отчет
по лабораторной работе №1
по дисциплине «Электротехническое материаловедение»
Тема: Исследование основных свойств проводниковых материалов
Санкт-Петербург
2025
Обработка результатов измерений
Пункт 1. Рассчитаем удельное сопротивление металлических проводников и сопротивление квадрата поверхности металлических пленок:
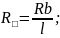
Пример расчета:
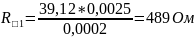
Материал |
R, Ом |
b, м |
l, м |
|
1 |
39,12 |
0,0025 |
0,0002 |
489 |
2 |
775,5 |
0,002 |
0,00325 |
477,2308 |
3 |
7601 |
0,0006 |
0,0095 |
480,0632 |
Таблица 1.1 Сопротивление квадрата поверхности металлических пленок.
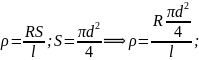
Пример расчета:
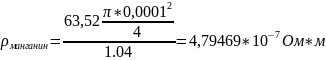
Материал |
R, Ом |
l, м |
d, м |
|
Манганин |
63,52 |
1,04 |
0,0001 |
4,795 |
Медь |
9,82 |
8,3 |
0,00013 |
0,157 |
Нихром |
2,66 |
0,9 |
0,0007 |
11,369 |
Константан |
198,51 |
1 |
0,0006 |
560,99 |
Никель |
2,43 |
1,5 |
0,00025 |
0,795 |
Таблица 1.2. Удельное сопротивление металлических проводников.
Пункт
2. Построим
графики температурных зависимостей
сопротивления
 для исследуемых резисторов:
для исследуемых резисторов:
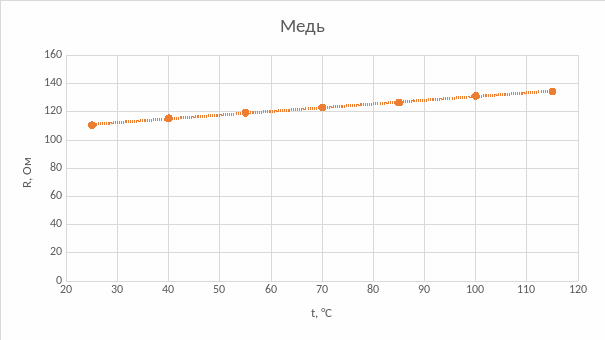
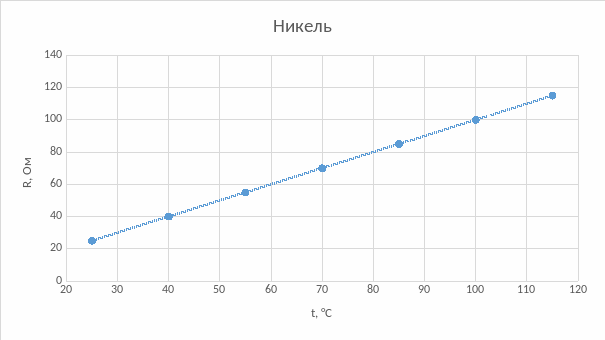
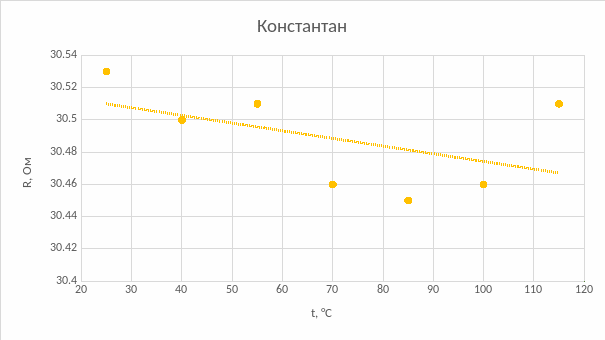
Пункт 3. Рассчитаем температурные коэффициенты удельного сопротивления металлов и сплавов:
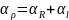

Отношение сопротивления к температуре найдем методом аппроксимации графиков зависимости , и эта величина останется постоянной для всех значений.
Для
никеля:
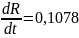
Для
меди:
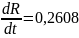
Для
константана:
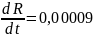
Температурные коэффициенты линейного расширения:
никель
–
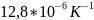
медь
–
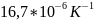
константан
–

Рассчитаем
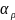 :
:
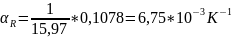

t, °C
|
Никель |
Медь |
Константан |
||||
R, Ом |
αρ*10-3, К-1 |
R, Ом |
αρ*10-3, К-1 |
R, Ом |
αρ*10-3, К-1 |
||
25 |
15,97 |
6,76 |
110,51 |
2,38 |
30,53 |
0,019 |
|
40 |
18,18 |
5,94 |
115,46 |
2,28 |
30,5 |
0,019 |
|
55 |
21,95 |
4,92 |
119,3 |
2,20 |
30,51 |
0,019 |
|
70 |
23,23 |
4,65 |
122,98 |
2,14 |
30,46 |
0,019 |
|
85 |
24,8 |
4,36 |
126,55 |
2,08 |
30,45 |
0,019 |
|
100 |
25,54 |
4,10 |
131,36 |
2 |
30,46 |
0,019 |
|
115 |
25,6 |
4,22 |
134,4 |
1,91 |
30,51 |
0,019 |
|
Таблица 2. Температурные коэффициенты удельного сопротивления металлов и сплавов.
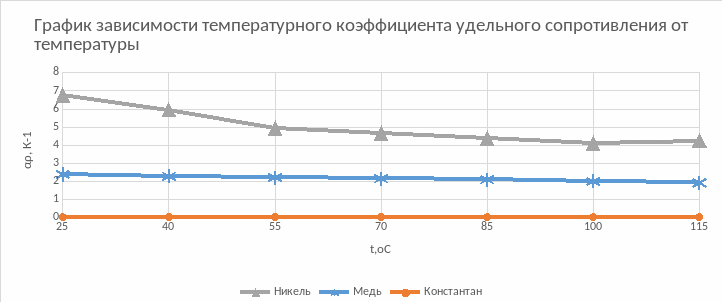
Пункт 4. Построим график зависимости температурного коэффициента удельного сопротивления к температуре:
Пункт 6. Рассчитаем зависимости удельного сопротивления и температурного коэффициента удельного сопротивления от состава для сплавов системы Cu–Ni при комнатной температуре:
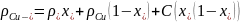
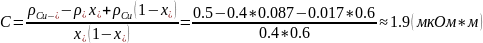
учитывая,
что
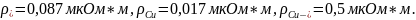
Значение температурного коэффициента рассчитаем по формуле
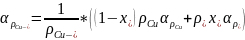
Рассчитаем значение коэффициентов для концентрации никеля 0,2:
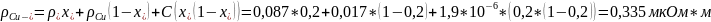

xNi |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
ρ*10-7, Ом*м |
0,17 |
3,35 |
5,01 |
5,15 |
3,77 |
0,87 |
αρ*10-3, К-1 |
2,37 |
0,44 |
0,52 |
0,72 |
1,27 |
6,76 |
Таблица 3. Удельное сопротивление и температурный коэффициент удельного сопротивления состава для сплавов системы Cu–Ni.
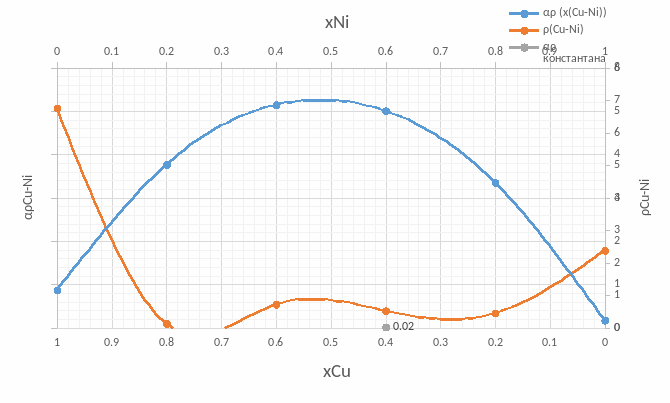
Пункт
7. Построим
график зависимости удельного сопротивления
сплава
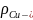 и температурного коэффициента удельного
сопротивления сплава
и температурного коэффициента удельного
сопротивления сплава
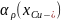 :
:
Пункт 8. Построим график зависимости термопар:
-
t гор, °C
t хол, °C
Δt, °C
ΔUAB, мВ
медь-железо
медь-константан
медь-манганин
25
26
-1
-0,12
-0,11
-0,09
40
28
12
0,44
0,42
-0,06
55
28
27
0,91
0,91
-0,05
70
28
42
1,3
1,35
-0,02
85
29
56
1,73
1,82
0,06
100
29
71
2,13
2,3
0,07
115
30
85
2,5
2,86
0,07
Таблица 4. Значения термоЭДС для различных термопар в зависимости от температуры
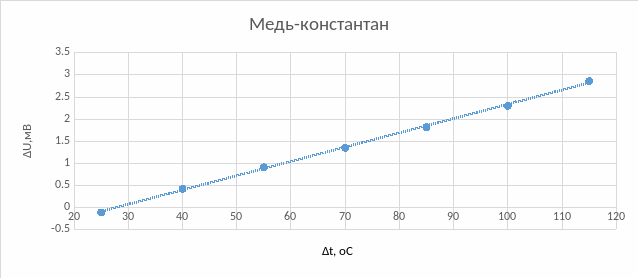
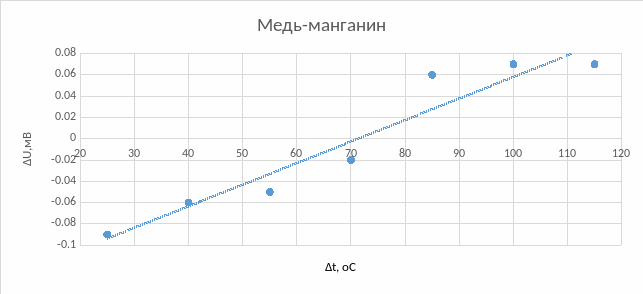
Вывод: в ходе лабораторной работы были исследованы температурные зависимости сопротивления трех проводников: никеля, меди и константана. В исследуемом температурном диапазоне сопротивление никеля и меди линейно возрастало, а сопротивление константана оставалось постоянным. Увеличение сопротивления объясняется следующим образом: атомы, находящиеся в узлах кристаллической решетки проводника, колеблются, при увеличении температуры амплитуда колебаний увеличивается; следовательно, носители заряда (электроны) чаще рассеиваются в процессе их направленного движения, соответственно уменьшается средняя длина свободного пробега и увеличивается сопротивление. Была рассмотрена зависимость удельного сопротивления и температурного коэффициента удельного сопротивления от состава системы медь-никель. Максимальное значение удельного сопротивления было получено при содержании примерно 50% меди и 50% никеля, т.к. искажение кристаллической решетки при этом максимально у обоих компонентов системы. Также получена температурная зависимость термоЭДС для термопар медь-железо, медь-константан, медь-манганин. Все термоЭДС линейно возрастают, но термоЭДС системы медь-манганин значительно медленнее. Основная причина: в металлах с увеличением
возникает контактная составляющая термоЭДС.

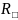 ,
Ом
,
Ом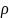 ,
Ом*м*10-7
,
Ом*м*10-7