Лаба 6

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Сыктывкарский государственный

университет имени Питирима Сорокина»

(ФГБОУ ВО «СГУ им. Питирима Сорокина»)

Институт точных наук и информационных технологий

Кафедра информационной безопасности

Лабораторная работа №6

Изучение спектра атома водорода

Работу выполнили студенты группы 121-Ибо

Проверил преподаватель

Дианов Михаил Юрьевич

Сыктывкар 2024

Цель работы: изучение закономерностей в спектре атома водорода, определение постоянной Ридберга, вычисление массы электрона и радиуса первой боровской орбиты.

Оборудование: монохроматор УМ-2, ртутная и водородная лампы.

Ход работы

Таблица 1.

Спектральные линии ртути	, Å	Показания шкалы барабана монохроматора, °
Красная	7081.9	3476
Жёлтая	5790.6	3147
Жёлтая	5769.6	3136
Зеленая	5460.7	2994
Голубая	4916.0	2770
Сине-голубая	5358.3	2356
Фиолетовая	4046.6	1907

Рис.1 График зависимости длины волны от показаний шкалы барабана монохроматора

Таблица 2.

	Спектральные линии атома водорода (серия Бальмера)
	красная — Hα		голубая — Hβ		фиолетовая — Hγ
Квантовые числа	m=2	n=3	m=2	n=4		m=2	n=5
Показания шкалы барабана монохроматора, °	3506		2450		1941
Длина волны, Å	7350,4		4385,0		4141.4

При помощи градуировочного графика (рис.1) составлены пропорции и найдены длины волн для красной, голубой и фиолетовой линий.

λ_α = 3504⋅7081.9/3376 ≈ 7350,4 Å

λ_β = 2469⋅4916.0/2768 ≈ 4385,0 Å

λ_γ = 1952⋅4046.6/1907 ≈ 4141.4 Å

(1)

По формуле (1) была найдена величина постоянной Ридберга для красной, голубой и фиолетовой линий, произведены вычисления среднего значения постоянной Ридберга:

R₁ = 1/(7350.4⋅10^-8⋅(1/2² - 1/3²)) ≈ 97953.9 см^-1

R₂ = 1/(4385,0⋅10^-8⋅(1/2² - 1/4²)) ≈ 121626.8 см^-1

R₃ = 1/(4141.4⋅10^-8⋅(1/2² - 1/5²)) ≈ 114983.0 см^-1

R_ср = (114982.971+121626.7579+97953.85285)/3 ≈ 111521.2 см^-1

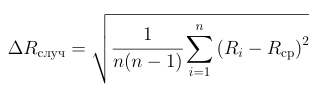(2)

По формуле (2) была вычислена случайная погрешность для постоянной Ридберга:

ΔRслуч = √((97953.9-111521.2)2+(121626.8-111521.2)2+(114983.0-111521.2)2)/(3⋅(3-1))) ≈ 7049.6 см-1

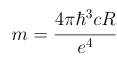(3)

По формуле (3) была оценена масса электрона:

m_e = (4⋅pi⋅(1.054⋅10^-27)³⋅3⋅10⁸⋅111521.2)/(4.8⋅10^-10)⁴ ≈ 9.4·10^-28 г

(4)

По формуле (4) рассчитан первый боровский радиус для атома водорода, оценены линейные размеры атома водорода:

a₀ = (1.054⋅10^-27)²/(9.3·10^-30⋅(4.8·10^-10)²) ≈ 0.517·10^-8 см = 0.517 Å

=> d = 2a₀ = 1.034 Å

a_теор = 0.530 Å

Рассмотрев значение первого боровского радиуса для атома водорода, можно сказать, что оно примерно совпадает с теоретическим.

Таблица 3.

Постоянная Ридберга, см−1				∆Rслуч, см−1		me, г		a0, Å		d, Å
R1	R2	R3	Rср
97953.9	121626.8	114983.0	111521.2		7049,6		9.4·10-28		0.517		1.034

(5)

По формуле (5) была найдена относительная погрешность определения первого боровского радиуса:

δa₀ = (|a₀-a_теор|/a_теор)⋅100% ≈ 1.1 %

Вывод: В ходе данной работы были изучены закономерности в спектре атома водорода; построен градуированный график зависимости длины волны от показаний шкалы барабана монохроматора, установлена прямая зависимость между этими величинами; были определены значения величин: постоянная Ридберга, масса электрона, радиус первой боровской орбиты, линейные размеры атома водорода, случайная погрешность для постоянной Ридберга и относительная погрешность определения первого боровского радиуса.