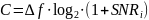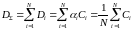Ресурсы.2

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Н.В. Апанасенко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

СТРАТЕГИИ РАСПРЕДЕЛЕНИЯ РЕСУРСНЫХ БЛОКОВ В ЦЕНТРАЛИЗОВАННОЙ СЕТИ СО СЛУЧАЙНЫМ ТРАФИКОМ

по курсу: МОДЕЛИРОВАНИЕ СИСТЕМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: получение навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда». Изучение свойств алгоритмов планирования ресурсов нисходящего кадра в подобных системах. Изучение стратегий распределения ресурсных блоков в централизованной сети со случайным трафиком

Индивидуальный вариант

Рисунок 1- Вариант задания

Пример расчета параметров моделируемой системы согласно индивидуальному варианту

Произведен расчет мощности шума по формуле 1

(1)

где -полоса пропускания канала связи,

- абсолютная температура,

k – постоянная Больцмана ,

- коэффициент теплового шума приемника .

Далее представлен расчет уровня потерь в канале связи для модели затухания в помещениях ITU

(2)

где K – коэффициент, зависящий от типа помещения (принят равным 29),

– переменная равная нулю

частота сигнала

-расстояние от базовой станции до абонента (взято 10)

Добавим к значению потерь случайную величину x=0,2

Для представления в линейном масштабе выполнен перевод из дБ в разы:

(3)

Рассчитана мощность сигнала, принятая АБ

(4)

где - мощность, излучаемая БС (Вт)

Вт

Произведен расчет отношения сигнал/шум по формуле

(5)

(раз)

Рассчитана пропускная способность канала связи по формуле

(6)

Анализ алгоритмов распределения ресурсов

Алгоритм Equal Blind

Данный алгоритм обеспечивает равные скорости передачи данных между всеми абонентами. Каждый абонент получает одинаковую долю ресурсов, которая определяется формулой

(7)

Скорость для абонента i может быть выражена как:

(8)

Алгоритм Maximum Throughput

Данный алгоритм максимизирует суммарную скорость передачи данных. Доля ресурса времени, выделяемая каждому абоненту, находится как

(9)

Алгоритм Proportion Fair

Данный алгоритм выделяет равные доли ресурсов всем абонентам. Доля ресурса времени, выделяемая каждому абоненту, находится как

(10)

Суммарная скорость:

(11)

Пример сгенерированных расположений абонентов

Написана программа, генерирующая координаты N абонентских устройств, равномерно распределенных внутри окружности с радиусом R, где в центре располагается БС. На рисунке 1 представлен пример расположения 500 абонентских устройств.

Листинг 1- Распределение абонентов вокруг БС

import numpy as np

import matplotlib.pyplot as plt

def distribute_ab(N, R):

# распределение по радиусу

d = np.sqrt(np.random.uniform(0, R**2, N).astype(float))

a = np.random.uniform(0, 2 * np.pi, N)

x = d * np.cos(a)

y = d * np.sin(a)

return x, y

# Параметры системы

N = 100

R = 20

P_TX = 0.05

f0 = 1200

delta_f = 180e3

T = 300

k_boltzmann = 1.38e-23

k_n = 4

num_slots = 10000

num_rb = 50

slot_duration = 0.5

# Распределение абонентов

x, y = distribute_ab(N, R)

# Визуализация расположения абонентов

plt.figure(figsize=(6, 6))

plt.gca().add_artist(plt.Circle((0, 0), R, fill=False, color='red')) # Круг

plt.scatter(x, y, color='green', s=10, label='Абоненты') # Абоненты

plt.scatter(0, 0, color='red', s=50, label='Базовая станция') # Базовая станция

plt.text(0, 0, 'БС', fontsize=12, ha='center', va='center', color='white')

plt.axis('equal')

plt.title('Расположение абонентов и базовой станции')

plt.xlabel('X')

plt.ylabel('Y')

plt.grid(True)

plt.legend()

plt.show()

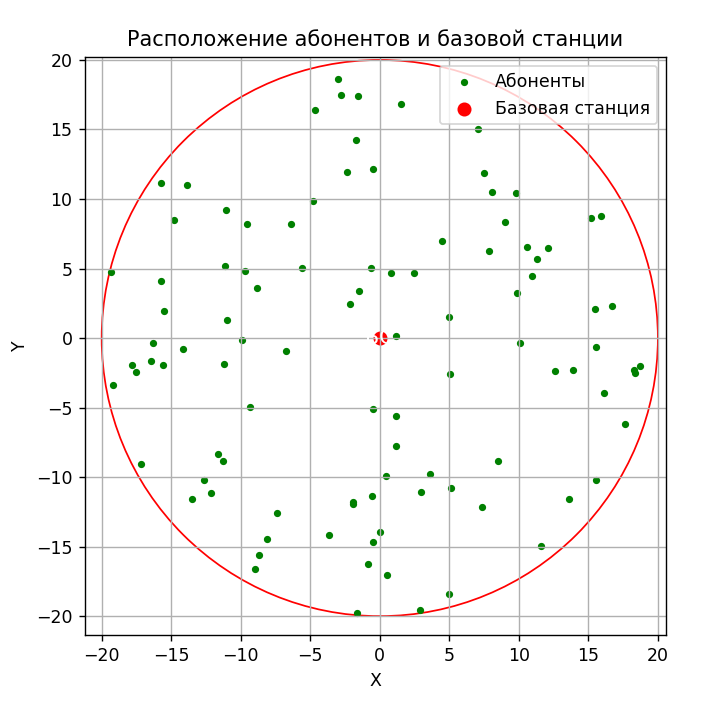
Рисунок 1 – Пример распределения абонентов

Далее напсиана функция, которая моделирует затухание сигнала в беспроводном канале связи. Затухание сигнала определяет, насколько сильно ослабевает радиосигнал при распространении от базовой станции к абонентам. Для каждого абонента рассчитывается расстояние до базовой станции.

Затем для каждого абонента, каждого ресурсного блока и каждого временного слота генерируется случайная величниа с помощью нормального распределения, с математическим ожиданием 0 и стандартым отклонением 1 (мера разброса значений относительно среднего). Итоговое затухание формируется путем добавления случайной составляющей к среднему затуханию. Для каждого абонента добавляется одно и то же среднее затухание ко всем его ресурсным блокам и временным слотам, но при этом для каждого ресурсного блока и слота добавляется своя уникальная случайная составляющая.

Каждый элемент L[i,j,k] представляет собой полное затухание сигнала в дБ для i-го абонента на j-м ресурсном блоке в k-м временном слоте. (Рисунок 2).

Листинг 2- Моделирование затухание сигнала

def calculate_path_loss(x, y, f0, num_slots, num_rb):

N = len(x)

r = np.sqrt(x**2 + y**2)

K = 29

L_mean = 20 * np.log10(f0) + K * np.log10(r) - 28

mean = 0

std = 1

z = np.random.normal(mean, std, (N, num_rb, num_slots))

# Формирование итогового затухания

L = np.zeros((N, num_rb, num_slots))

for i in range(N):

L[i, :, :] = L_mean[i] + z[i, :, :]

return L

Для визуализации распределния затухания сигнала построена гистограмма потерь сигнала для первого абонента в первом ресурсном блоке на протяжении всех временных слотов моделирования. (Рисунок 2).

Листинг 3- Гистограмма распределения затухания сигнала

path_loss = calculate_path_loss(x, y, f0, num_slots, num_rb)

# Гистограмма потерь сигнала

plt.figure(figsize=(8, 5))

path_loss_data = path_loss[0, 0, :]

plt.hist(path_loss_data, bins=25, color='indigo', alpha=0.7, label='Гистограмма потерь')

plt.title('Распределение потерь сигнала')

plt.xlabel('Затухание сигнала [дБ]')

plt.ylabel('Частота')

plt.grid(True)

plt.show()

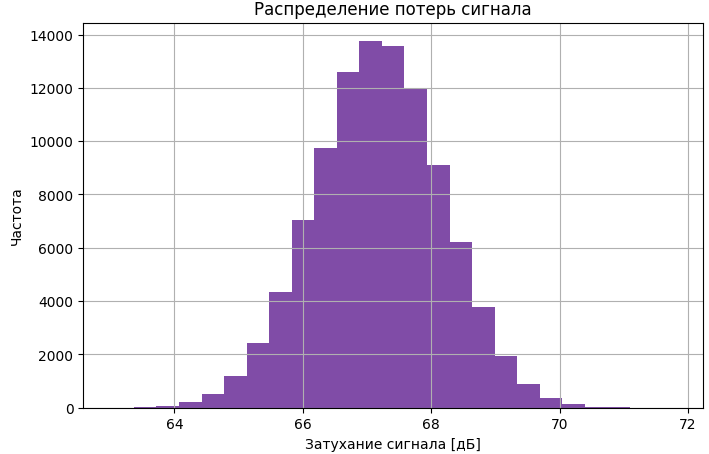
Рисунок 2- Гистограммы часто встречаемых значений потерь для первого абонента

По гистограмме видно, что распределение потерь имеет форму, близкую к нормальному распределению, что говорит о корректности моделирования случайной составляющей затухания сигнала.

Затем написана функция generate_packets выполняющая генерацию случайного потока пакетов данных для каждого абонента в системе. Она принимает количество абонентов , количество временных слотов и параметр λ, который определяет интенсивность потока пакетов. Для моделирования случайного поступления пакетов данных используется распределение Пуассона. После генерации количества пакетов выполнен перевод в байты.

Листинг 4- Функция generate_packets выполняющая генерацию случайного потока пакетов данных

def generate_packets(N, num_slots, lambda_param):

# Генерация пуассоновского потока пакетов

packets = np.random.poisson(lambda_param, (N, num_slots))

v = packets * 1024

return v

Далее написана функция расчета максимальных скоростей передачи данных для каждого абонента, ресурсного блока и временного слота.

Листинг 5- Функция calculate_max_speeds для расчета максимальных скоростей

def calculate_max_speeds(P_TX, path_loss, delta_f, k_n, T, k_boltzmann):

P_N = k_n * T * delta_f * k_boltzmann

# Перевод потерь из дБ в разы

path_loss_linear = 10 ** (path_loss / 10)

P_RX = P_TX / path_loss_linear

SNR = P_RX / P_N

C = delta_f * np.log2(1 + SNR)

return C

Затем в программе реализован расчет приоритетов для каждого абонента на каждый ресурсный блок на каждом слоте для трех алгоритмов распределения ресурсов. Equal Blind стремится обеспечить равномерное распределение ресурсов между пользователями. Для этого алгоритма приоритет обратно пропорционален средней скорости. Чем ниже скорость, с которой БС взаимодействовала с пользователем, тем выше приоритет. К средней скорости доабавляется наименьшая величина, чтобы избежать деления на ноль в случае, если абоненты только вошли в систему и невозможно отследить скорость их взаимодействия с базовой станцией.

Для алгоритма Maximum Throughput приоритет равен текущей достижимой скорости передачи данных. Ресурсы выделяются абоненту с наилучшими условиями канала связи.

Proportional Fair делает так, чтобы количество отданных ресурсов было одинаковым. учитывая как текущую скорость передачи, так и историю обслуживания пользователя. Приоритет определяется как отношение текущей пропускной способности передачи к средней скорости, с которой абонент получал данные.

Средняя скорость рассчитывается на интервале времени 1 секунда (что соответствует 2000 слотов при длительности слота 0.5 мс). Для каждого абонента суммируется объем переданных данных на выделенных ему ресурсных блоках за последнюю секунду, и полученная сумма делится на длительность интервала усреднения. При этом учитывается история выделения ресурсов - суммирование происходит только по тем слотам, в которых абоненту были выделены ресурсные блоки.

Листинг 5- Расчет приоритетов

def calculate_priorities(C, R, algorithm):

P = np.zeros_like(C)

# Для каждого ресурсного блока

for j in range(C.shape[1]):

if algorithm == 'EB':

P[:, j] = 1.0 / (R + 1e-10)

elif algorithm == 'MT':

P[:, j] = C[:, j]

elif algorithm == 'PF':

P[:, j] = C[:, j] / (R + 1e-10)

return P

Листинг 6- Расчет средней скорости

def calculate_average_rate(D_history, allocation_history, V, slot_duration, window_size=1.0):

N, num_slots = D_history.shape

y_slot = int(window_size / (slot_duration/1000.0))

R = np.zeros(N)

for i in range(N):

start_slot = max(0, num_slots - y_slot)

sum_data = 0

# Суммирование по слотам и ресурсным блокам

for m in range(start_slot, num_slots):

for j in range(V.shape[1]): # по всем ресурсным блокам

if allocation_history[i, m] == 1: # если ресурс был выделен

sum_data += V[i, j, m]

actual_window_size = (num_slots - start_slot) * slot_duration / 1000.0

R[i] = sum_data / actual_window_size if actual_window_size > 0 else 0

return R

Листинг 7- Расчет объема данных

def calculate_volume_data(C, slot_duration):

return C * slot_duration / 1000

Для исследования зависимости среднего суммарного объема данных в буфере от λ. Пострены графики, где по оси X откладывается интенсивность входного потока λ (пакетов/слот), а по оси Y - средний размер буфера в байтах (Рисунок 3-6).

Рисунок 3 – График зависимости среднего объема в буфере от интенсивности входного потока при N=2

Алгоритм Maximum Throughput показывает наилучшую производительность при высокой нагрузке, обеспечивая наименьший размер буфера. Алгоритм Proportional Fair демонстрирует средние показатели.

Equal Blind показывает наихудшую производительность при высокой нагрузке, возможно, из-за того, что алгоритм не учитывает текущее состояние канала при распределении ресурсов, что приводит к неоптимальному использованию доступной пропускной способности.

Рисунок 4 – График зависимости среднего объема в буфере от интенсивности входного потока при N=8

При восьми абонетах расчетное пороговое значение составляло 1,58 пакетов/слот. График наглядно демонстрирует, что после превышения этого значения начинается устойчивый рост среднего буфера. Все три алгоритма планирования показывают схожую динамику накопления данных, что объясняется более равномерным распределением ресурсов между большим количеством пользователей.

Рисунок 5 – График зависимости среднего объема в буфере от интенсивности входного потока при N=16

На графике видно, что даже при относительно небольших значениях λ (около 1 пакета/слот) начинается заметное накопление данных в буферах. Это объясняется тем, что на каждого пользователя приходится существенно меньшая доля общей пропускной способности системы.

Рисунок 6- График зависимости среднего объема в буфере от интенсивности входного потока при N=32

При N=32 пользователя наблюдается практически линейный рост среднего буфера начиная с самых малых значений интенсивности входящего потока. Различия между алгоритмами практически нет. В этих условиях даже оптимальное планирование ресурсов не может предотвратить рост очередей, так как общая нагрузка значительно превышает возможности системы.

Выводы:

В данной лабораторной работе было проведено исследование системы различными алгоритмами планирования ресурсов. Разработанная программа позволила смоделировать работу системы с учетом реальных физических параметров распространения сигнала и различных алгоритмов распределения ресурсов.

При двух пользователях наблюдается четкая граница начала перегрузки системы около 6 пакетов/слот, причем алгоритм Maximum Throughput показал наилучшую производительность при высокой нагрузке. При увеличении числа пользователей до 8 и 16 пороги перегрузки снижались в соответствии с расчетами, а различия между алгоритмами становились менее выраженными.

При максимальном количестве пользователей система демонстрирует практически линейный рост очередей с самых малых значений интенсивности входного потока, что объясняется значительным уменьшением доступных ресурсов на одного пользователя. В данном случае различия между алгоритмами планирования становятся минимальными, так как система работает в режиме сильной перегрузки.

ПРИЛОЖЕНИЕ А

import numpy as np

import matplotlib.pyplot as plt

from scipy.stats import poisson

N = 100

R = 20 #

P_TX = 0.05

f0 = 1200 #

delta_f = 180e3

# Параметры канала связи

T = 300 # Температура [К]

k_boltzmann = 1.38e-23 # Постоянная Больцмана [Дж/К]

k_n = 4 # Коэффициент шума

# Параметры временных слотов

num_slots = 100 # Количество временных слотов

num_rb = 50 # Количество ресурсных блоков

slot_duration = 0.5 # Длительность слота [мс]

def distribute_ab(N, R):

# Равномерное распределение по радиусу

d = np.sqrt(np.random.uniform(0, R**2, N))

# Случайный угол для каждого абонента

a = np.random.uniform(0, 2 * np.pi, N)

# Преобразование в декартовы координаты

x = d * np.cos(a)

y = d * np.sin(a)

return x, y

def calculate_path_loss(x, y, f0, num_slots, num_rb):

N = len(x)

# Расчет расстояния до базовой станции

r = np.sqrt(x**2 + y**2)

K = 29 # Коэффициент для типа помещения

# Расчет среднего затухания

L_mean = 20 * np.log10(f0) + K * np.log10(r) - 28

# Добавление случайной составляющей

z = np.random.normal(0, 1, (N, num_rb, num_slots))

L = np.zeros((N, num_rb, num_slots))

for i in range(N):

L[i, :, :] = L_mean[i] + z[i, :, :]

return L

def calculate_max_speeds(P_TX, path_loss, delta_f, k_n, T, k_boltzmann):

P_N = k_n * T * delta_f * k_boltzmann

# Перевод потерь из дБ в разы

path_loss_linear = 10 ** (path_loss / 10)

P_RX = P_TX / path_loss_linear

SNR = P_RX / P_N

C = delta_f * np.log2(1 + SNR)

return C

def calculate_volume_data(C, slot_duration):

return C * slot_duration / 1000

def calculate_total_volume(V):

N, num_rb, num_slots = V.shape

r = np.zeros((N, num_slots))

for i in range(N):

for k in range(num_slots):

r[i, k] = np.sum(V[i, :, k])

return r

def generate_packets(N, num_slots, lambda_param):

packets = np.random.poisson(lambda_param, (N, num_slots))

return packets * 1024 * 8 # Размер пакета 1 КБ = 1024 байт, переводим в биты

def calculate_average_rate(D_history, allocation_history, V, slot_duration, window_size=1.0):

N, num_slots = D_history.shape

y_slot = int(window_size / (slot_duration/1000.0)) # переводим в секунды

R = np.zeros(N)

for i in range(N):

start_slot = max(0, num_slots - y_slot)

sum_data = 0

# Суммирование по слотам и ресурсным блокам

for m in range(start_slot, num_slots):

for j in range(V.shape[1]): # по всем ресурсным блокам

if allocation_history[i, m] == 1: # если ресурс был выделен

sum_data += V[i, j, m]

actual_window_size = (num_slots - start_slot) * slot_duration / 1000.0

R[i] = sum_data / actual_window_size if actual_window_size > 0 else 0

return R

def calculate_priorities(C, R, algorithm):

P = np.zeros_like(C)

for j in range(C.shape[1]):

if algorithm == 'EB':

P[:, j] = 1.0 / (R + 1e-10)

elif algorithm == 'MT':

P[:, j] = C[:, j]

elif algorithm == 'PF':

P[:, j] = C[:, j] / (R + 1e-10)

return P

def simulate(x, y, P_TX, f0, delta_f, k_n, T, k_boltzmann, num_slots, num_rb, slot_duration, lambda_param, algorithm='PF'):

N = len(x)

buffers = np.zeros(N)

buffer_history = []

R = np.zeros(N)

path_loss = calculate_path_loss(x, y, f0, num_slots, num_rb)

channel_capacity = calculate_max_speeds(P_TX, path_loss, delta_f, k_n, T, k_boltzmann)

data_volume = calculate_volume_data(channel_capacity, slot_duration)

# Генерация входящего трафика для всех слотов

incoming_traffic = generate_packets(N, num_slots, lambda_param)

# Моделирование по временным слотам

for current_slot in range(num_slots):

# Добавление новых пакетов в буферы

buffers += incoming_traffic[:, current_slot]

# Обновление средних скоростей пользователей

if current_slot > 0:

transmitted_data_history = np.zeros((N, current_slot))

resource_allocation_history = np.zeros((N, current_slot))

R = calculate_average_rate(transmitted_data_history,

resource_allocation_history,

data_volume,

slot_duration)

# Распределение ресурсных блоков

transmitted_data = np.zeros(N)

for rb in range(num_rb):

# Определение пользователей с непустыми буферами

active_users = buffers > 0

if not np.any(active_users):

continue

priorities = calculate_priorities(channel_capacity[:, :, current_slot],

R,

algorithm)

current_priorities = priorities[:, rb].copy()

current_priorities[~active_users] = -np.inf

selected_user = np.argmax(current_priorities)

# Передача данных выбранному пользователю

available_data = data_volume[selected_user, rb, current_slot]

actual_transmission = min(available_data, buffers[selected_user])

buffers[selected_user] -= actual_transmission

transmitted_data[selected_user] += actual_transmission

# Сохранение статистики текущего слота

buffer_history.append(np.sum(buffers))

return np.array(buffer_history)

# Параметры симуляции

lambda_values = np.linspace(0.0, 8.0, 10)

N_values = [2, 8, 16, 32]

algorithms = ['PF', 'MT', 'EB']

algorithm_colors = {

'PF': 'red',

'MT': 'lime',

'EB': 'indigo'

}

for N in N_values:

plt.figure(figsize=(10, 6))

x, y = distribute_ab(N, R)

for algorithm in algorithms:

buffer_data = []

for lambda_param in lambda_values:

total_data = simulate(x, y, P_TX, f0, delta_f, k_n, T, k_boltzmann,

num_slots, num_rb, slot_duration, lambda_param, algorithm)

buffer_data.append(np.mean(total_data))

plt.plot(lambda_values, buffer_data,

color=algorithm_colors[algorithm],

label=algorithm,

linewidth=2,

marker='o',

markersize=6,

linestyle='-')

plt.title(f'N={N} пользователей')

plt.xlabel('λ (пакетов/слот)')

plt.ylabel('Средний буфер (МБ)')

plt.legend()

plt.grid(True)

plt.tight_layout()

plt.show()