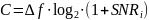Ресурсы1.2

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Н.В. Апанасенко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ НИСХОДЯЩЕГО КАДРА В ТЕЛЕКОММУНИКАЦИОННЫХ СЕТЯХ

по курсу: МОДЕЛИРОВАНИЕ СИСТЕМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: получение навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда». Изучение свойств алгоритмов планирования ресурсов нисходящего кадра в подобных системах, на примере алгоритмов Equal Blind, Proportion fair, Maximum Throughput.

Индивидуальный вариант

Рисунок 1- Вариант задания

Пример расчета параметров моделируемой системы согласно индивидуальному варианту

Произведен расчет мощности шума по формуле 1

(1)

где -полоса пропускания канала связи,

- абсолютная температура,

k – постоянная Больцмана ,

- коэффициент теплового шума приемника .

Далее представлен расчет уровня потерь в канале связи для модели затухания в помещениях ITU

(2)

где K – коэффициент, зависящий от типа помещения (принят равным 29),

– переменная равная нулю

частота сигнала

-расстояние от базовой станции до абонента (взято 10)

2

Для представления в линейном масштабе выполнен перевод из дБ в разы:

(3)

Рассчитана мощность сигнала, принятая АБ

(4)

где - мощность, излучаемая БС (Вт)

Вт

Произведен расчет отношения сигнал/шум по формуле

(5)

(раз)

Рассчитана пропускная способность канала связи по формуле

(6)

Анализ алгоритмов распределения ресурсов

Алгоритм Equal Blind

Данный алгоритм обеспечивает равные скорости передачи данных между всеми абонентами. Каждый абонент получает одинаковую долю ресурсов, которая определяется формулой

(7)

Скорость для абонента i может быть выражена как:

(8)

Алгоритм Maximum Throughput

Данный алгоритм максимизирует суммарную скорость передачи данных. Доля ресурса времени, выделяемая каждому абоненту, находится как

(9)

Алгоритм Proportion Fair

Данный алгоритм выделяет равные доли ресурсов всем абонентам. Доля ресурса времени, выделяемая каждому абоненту, находится как

(10)

Суммарная скорость:

(11)

Пример сгенерированных расположений абонентов

Написана программа, генерирующая координаты N абонентских устройств, равномерно распределенных внутри окружности с радиусом R, где в центре располагается БС. На рисунке 1 представлен пример расположения 500 абонентских устройств.

Листинг 1- Распределение абонентов вокруг БС

import numpy as np

import matplotlib.pyplot as plt

def distribute_ab(N, R):

# распределение по радиусу

d = np.sqrt(np.random.uniform(0, R**2, N).astype(float))

a = np.random.uniform(0, 2 * np.pi, N)

x = d * np.cos(a)

y = d * np.sin(a)

return x, y

# Параметры системы

N = 500

R = 20 # Радиус окружности

P_TX = 0.05 # Мощность передачи

f0 = 2400 # Частота сигнала

delta_f = 20e6 # Полоса пропускания

T = 300 # Температура

k = 1.38e-23 # Постоянная Больцмана

k_n=4

# Распределение абонентов

x, y = distribute_ab(N, R)

# Визуализация расположения абонентов

plt.figure(figsize=(6, 6))

plt.gca().add_artist(plt.Circle((0, 0), R, fill=False, color='red')) # Круг

plt.scatter(x, y, color='green', s=10, label='Абоненты') # Абоненты

plt.scatter(0, 0, color='red', s=50, label='Базовая станция') # Базовая станция

plt.text(0, 0, 'БС', fontsize=12, ha='center', va='center', color='white')

plt.axis('equal')

plt.title('Расположение абонентов и базовой станции')

plt.xlabel('X')

plt.ylabel('Y')

plt.grid(True)

plt.legend()

plt.show()

Рисунок 1 – Пример распределения абонентов

Для визуализации равномерности распределения построена гистограмма, которая показывает, как часто встречаются определённые диапазоны значений среди сгенерированных чисел (Рисунок 2).

Листинг 2- Построение гистограммы

# вычисление расстояний от центра до АБ

r = np.sqrt(x**2 + y**2)

# Гистограмма расстояний от центра

plt.figure(figsize=(8, 5))

plt.hist(r, bins=25, color='indigo', alpha=0.7, label='Гистограмма расстояний')

plt.title('Распределение расстояний от центра')

plt.xlabel('Расстояние')

plt.ylabel('Частота')

plt.grid(True)

plt.show()

Рисунок 2- Гистограммы часто встречаемых значений расстояний

Гистограмма показывает линейный рост, это говорит о том, что количество абонентов увеличивается с увеличением расстояния от центра. Это связано с тем, что площадь внешних областей круга больше, чем площадь внутренних, и, следовательно, вероятность нахождения абонента в этих областях выше.

Результаты моделирования

Для сравнения трех разных алгоритмов распределения ресурсов, для разного количества абонентов N [= 1, 2, 4, 8, …, 64] выполняется 100 симуляций. В каждой симуляции абоненты распределяются в круге с радиусом R, для каждого абонента рассчитывается максимальная скорость передачи данных. Затем применяются алгоритмы распределения ресурсов, и рассчитываются метрики для анализа производительности (суммарная скорость, средняя скорость, минимальная скорость). После выполнения всех симуляций результаты метрик усредняются.

Результаты моделирования визуализируются с помощью построения графиков зависимости средней суммарной скорости, средней скорости и средней минимальной скорости от количества абонентов (Рисунок 3-5).

Листинг 3- Функции алгоритмов, моделирование распределения, построение графиков

def calculate_max_speeds(x, y, P_TX, f0, delta_f, k_n, T, k):

distances = np.sqrt(x**2 + y**2)

# Расчет мощности шума

P_N = k_n * T * delta_f*k

K = 29 # Коэффициент для типа помещения

Pf_n = 0

loss_db = 20 * np.log10(f0) + K * np.log10(distances) + Pf_n - 28

loss = 10 ** (loss_db / 10) # Перевод из дБ в линейный масштаб

# Расчет отношения сигнал/шум

P_RX = (P_TX / loss)

SNR = P_RX / P_N

С = delta_f * np.log2(1 + SNR)

return С

def equal_blind(C):

# равные скорости

alpha = (1 / C) / np.sum(1 / C)

return alpha

def maximum_throughput(C):

# максимальная суммарная скорость

alpha = np.zeros_like(C)

alpha[np.argmax(C)] = 1

return alpha

def proportion_fair(C):

# равные доли ресурсов

alpha = np.ones_like(C) / len(C)

return alpha

def calculate_metrics(C, alpha):

fact_speeds = alpha * C

total_speed = np.sum(fact_speeds) / 1e6

avg_speed = np.mean(fact_speeds) / 1e6

min_speed = np.min(fact_speeds) / 1e6

return total_speed, avg_speed, min_speed

# моделирование

def simulate(N_values, num_simulations=100):

results = {'equal_blind': {'sum': [], 'avg': [], 'min': []},

'maximum_throughput': {'sum': [], 'avg': [], 'min': []},

'proportion_fair': {'sum': [], 'avg': [], 'min': []}}

for N in N_values:

sum_equal_blind, avg_equal_blind, min_equal_blind = [], [], []

sum_maximum_throughput, avg_maximum_throughput, min_maximum_throughput = [], [], []

sum_proportion_fair, avg_proportion_fair, min_proportion_fair = [], [], []

for _ in range(num_simulations):

x, y = distribute_ab(N, R)

speeds = calculate_max_speeds(x, y, P_TX, f0, delta_f, k_n, T, k)

# Алгоритмы

alpha_equal_blind = equal_blind(speeds)

alpha_maximum_throughput = maximum_throughput(speeds)

alpha_proportion_fail = proportion_fair(speeds)

# Расчет метрик

sum_equal, avg_equal, min_equal = calculate_metrics(speeds, alpha_equal_blind)

total_maximum, avg_maximum, min_maximum = calculate_metrics(speeds, alpha_maximum_throughput)

total_proportion, avg_proportion, min_proportion = calculate_metrics(speeds, alpha_proportion_fail)

# Сохранение результатов

sum_equal_blind.append(sum_equal)

avg_equal_blind.append(avg_equal)

min_equal_blind.append(min_equal)

sum_maximum_throughput.append(total_maximum)

avg_maximum_throughput.append(avg_maximum)

min_maximum_throughput.append(min_maximum)

sum_proportion_fair.append(total_proportion)

avg_proportion_fair.append(avg_proportion)

min_proportion_fair.append(min_proportion)

# Усреднение результатов

results['equal_blind']['sum'].append(np.mean(sum_equal_blind))

results['equal_blind']['avg'].append(np.mean(avg_equal_blind))

results['equal_blind']['min'].append(np.mean(min_equal_blind))

results['maximum_throughput']['sum'].append(np.mean(sum_maximum_throughput))

results['maximum_throughput']['avg'].append(np.mean(avg_maximum_throughput))

results['maximum_throughput']['min'].append(np.mean(min_maximum_throughput))

results['proportion_fair']['sum'].append(np.mean(sum_proportion_fair))

results['proportion_fair']['avg'].append(np.mean(avg_proportion_fair))

results['proportion_fair']['min'].append(np.mean(min_proportion_fair))

return results

N_values = [1, 2, 4, 8, 16, 32, 64]

num_simulations = 100

results = simulate(N_values, num_simulations)

# Зависимость средней суммарной скорости от количества абонентов

plt.figure(figsize=(10, 6))

plt.plot(N_values, results['equal_blind']['sum'], label='Equal Blind', color='indigo')

plt.plot(N_values, results['maximum_throughput']['sum'], label='Maximum Throughput', color='lime')

plt.plot(N_values, results['proportion_fair']['sum'], label='Proportion Fair', color='red')

plt.title('Зависимость средней суммарной скорости от количества абонентов')

plt.xlabel('Количество абонентов (N)')

plt.ylabel('Средняя суммарная скорость (бит/с)')

plt.grid(True)

plt.legend()

plt.show()

# Зависимость средней скорости от количества абонентов

plt.figure(figsize=(10, 6))

plt.plot(N_values, results['equal_blind']['avg'], label='Equal Blind', color='indigo')

plt.plot(N_values, results['maximum_throughput']['avg'], label='Maximum Throughput', color='lime')

plt.plot(N_values, results['proportion_fair']['avg'], label='Proportion Fair', color='red')

plt.title('Зависимость средней скорости от количества абонентов')

plt.xlabel('Количество абонентов (N)')

plt.ylabel('Средняя скорость (бит/с)')

plt.grid(True)

plt.legend()

plt.show()

# Зависимость средней минимальной скорости от количества абонентов

plt.figure(figsize=(10, 6))

plt.plot(N_values, results['equal_blind']['min'], label='Equal Blind', color='indigo')

plt.plot(N_values, results['maximum_throughput']['min'], label='Maximum Throughput', color='lime')

plt.plot(N_values, results['proportion_fair']['min'], label='Proportion Fair', color='red')

plt.title('Зависимость средней минимальной скорости от количества абонентов')

plt.xlabel('Количество абонентов (N)')

plt.ylabel('Средняя минимальная скорость (бит/с)')

plt.grid(True)

plt.legend()

plt.show()

Рисунок 3 – График зависимости средней суммарной скорости передачи данных от количества абонентов

Из графика, представленного на рисунке 3 видно, что алгоритм Maximum Throughput обеспечивает наибольшую суммарную скорость среди всех алгоритмов, так как все ресурсы выделяются абоненту с максимальной скоростью. С увеличением количества абонентов, суммарная скорость растет, возможно, потому что вероятность появления абонента с высокой скоростью возрастает.

Proportion Fair показывает стабильную максимальную скорость передачи, которая практически не изменяется с ростом количества абонентов, так как алгоритм разделяет ресурсы поровну между всеми абонентами.

Алгоритм Equal Blind показал самую наименьшую максимальную скорость, так как предоставляет равные скорости для всех абонентов.

У алгоритмов Proportion Fair и Equal Blind после 8 абонентов суммарная скорость перестает расти, возможно, в системе появляются абоненты на большем удалении от БС с минимальной скоростью передачи. Эти абоненты ограничивают суммарную скорость системы, так как ресурсы выделяются и им.

Рисунок 4 – График зависимости средней скорости передачи данных от количества абонентов

У всех алгоритмов средняя скорость снижается с увеличением количества абонентов. У алгоритма Maximum Throughput c увеличением абонентов средняя скорость чуть выше, чем у других. Алгоритмы Proportion Fair и Equal Blind ведут себя схожим образом, так как в обоих случаях ресурсы распределяются равномерно, что приводит к схожим значениям средней скорости.

Рисунок 5 – График зависимости средней минимальной скорости передачи данных от количества абонентов

У алгоритма Maximum Throughput, так как все ресурсы выделяются одному абоненту с наилучшими условиями связи, с ростом количества абонентов (N>1) минимальная скорость равна 0.

Алгоритм Equal Blind обеспечивает чуть более высокую минимальную скорость, чем Proportion Fair, так как предоставляет всем абонентам равные скорости, средняя скорость будет равна минимальной.Оба алгоритма демонстрируют снижение средней минимальной скорости с ростом числа абонентов.

Для проверки правильности разработанной программы смоделирована работа системы для 4 абонентов и произведен выывод расстояний, максимальных скоростей, на какие доли алгоритмы распределили ресурсы и суммарная, средняя и минимальная скорости (Рисунок 6).

Рисунок 6- Результаты распределения ресурсов для 4 абонентов

При расчете вручную максимальная скорость для абонента расоплложенного на расстоянии 10 метров от БС получилась 287 Мбит/с. На рисунке 7 видно, что для большиз расстояний максимальные скорости меньше 287 Мбит/с, что подтверждает тот факт, что с увеличением расстояния от базовой станции максимальная скорость уменьшается.

Скорости варьируются в пределах от 240 до 278 Мбит/с и видно, что они отражают зависимость скорости от расстояния. Алгоритм Equal Blind дает абоненту с наименьшей скоростью наиболшую долю ресурсов, чтобы обеспечить равные скорости передачи данных для всех абонетов. По выведенным метрикам видно, что минимальная скорость равна средней, значит все абоненты получают одинаковую скорость.

Maximum Throughput всересурсы выделяют одному абоненту с наибольшей скоростью. Суммарная скорость равна скорости абонента с максимальной пропускной способностью.

При использовании алгоритма Proportion Fair все абоненты получают равные доли ресурсов.

Выводы:

В ходе лабораторной работы были проанализированы три алгоритма распределения ресурсов Maximum Throughput, Proportion Fair и Equal Blind.

Алгоритм Maximum Throughput демонстрирует наибольшую суммарную скорость передачи данных, так как все ресурсы выделяются абоненту с наилучшими условиями связи (максимальной скоростью). С увеличением количества абонентов суммарная скорость растет, так как вероятность появления абонента с высокой скоростью увеличивается. Средняя скорость снижается с ростом числа абонентов, но остается чуть выше, чем у других алгоритмов. Минимальная скорость равна нулю, если абонентов больше одного, так как остальные абоненты не получают ресурсов.

Алгоритмы Proportion Fair и Equal Blind направлены на обеспечение более равномерного распределения ресурсов. Proportion Fair распределяет ресурсы поровну между всеми абонентами, что обеспечивает стабильную суммарную скорость, но с увеличением количества абонентов средняя и минимальная скорость снижаются из-за деления ресурсов между большим числом пользователей. Equal Blind обеспечивает равные скорости для всех абонентов. Оба алгоритма демонстрируют снижение минимальной скорости с ростом числа абонентов, так как ресурсы распределяются между всеми, включая тех, кто находится в условиях хуже, чем другие абоненты.

ПРИЛОЖЕНИЕ А

Программная реализация моделирования распределения ресурсов в беспроводной сети

import numpy as np

import matplotlib.pyplot as plt

def distribute_ab(N, R):

# распределение по радиусу

d = np.sqrt(np.random.uniform(0, R**2, N).astype(float))

a = np.random.uniform(0, 2 * np.pi, N)

x = d * np.cos(a)

y = d * np.sin(a)

return x, y

def calculate_max_speeds(x, y, P_TX, f0, delta_f, k_n, T, k):

distances = np.sqrt(x**2 + y**2)

P_N = k_n * T * delta_f * k

K = 29 # Коэффициент для типа помещения

Pf_n = 0

loss_db = 20 * np.log10(f0) + K * np.log10(distances) + Pf_n - 28

loss = 10 ** (loss_db / 10) # Перевод из дБ в линейный масштаб

P_RX = (P_TX / loss)

SNR = P_RX / P_N

С = delta_f * np.log2(1 + SNR)

return С

def equal_blind(C):

# равные скорости

alpha = (1 / C) / np.sum(1 / C)

return alpha

def maximum_throughput(C):

# максимальная суммарная скорость

alpha = np.zeros_like(C)

alpha[np.argmax(C)] = 1

return alpha

def proportion_fair(C):

# равные доли ресурсов

alpha = np.ones_like(C) / len(C)

return alpha

def calculate_metrics(C, alpha):

fact_speeds = alpha * C

total_speed = np.sum(fact_speeds) / 1e6

avg_speed = np.mean(fact_speeds) / 1e6

min_speed = np.min(fact_speeds) / 1e6

return total_speed, avg_speed, min_speed

# Параметры системы

N = 500

R = 20 # Радиус окружности

P_TX = 0.05 # Мощность передачи

f0 = 2400 # Частота сигнала

delta_f = 20e6 # Полоса пропускания

T = 300

k = 1.38e-23

k_n = 4

# Распределение абонентов

x, y = distribute_ab(N, R)

# Визуализация

plt.figure(figsize=(6, 6))

plt.gca().add_artist(plt.Circle((0, 0), R, fill=False, color='red'))

plt.scatter(x, y, color='green', s=10, label='Абоненты')

plt.scatter(0, 0, color='red', s=50, label='Базовая станция')

plt.text(0, 0, 'БС', fontsize=12, ha='center', va='center', color='white')

plt.title('Расположение абонентов и базовой станции')

plt.xlabel('X')

plt.ylabel('Y')

plt.grid(True)

plt.legend()

plt.show()

# Вычисление расстояний от центра

r = np.sqrt(x**2 + y**2)

# Гистограмма расстояний от центра

plt.figure(figsize=(8, 5))

plt.hist(r, bins=25, color='indigo', alpha=0.7, label='Гистограмма расстояний') # Убрано density=True

plt.title('Распределение расстояний от центра')

plt.xlabel('Расстояние')

plt.ylabel('Частота')

plt.grid(True)

plt.show()

# моделирование

def simulate(N_values, num_simulations=100):

results = {'equal_blind': {'sum': [], 'avg': [], 'min': []},

'maximum_throughput': {'sum': [], 'avg': [], 'min': []},

'proportion_fair': {'sum': [], 'avg': [], 'min': []}}

for N in N_values:

sum_equal_blind, avg_equal_blind, min_equal_blind = [], [], []

sum_maximum_throughput, avg_maximum_throughput, min_maximum_throughput = [], [], []

sum_proportion_fair, avg_proportion_fair, min_proportion_fair = [], [], []

for _ in range(num_simulations):

x, y = distribute_ab(N, R)

speeds = calculate_max_speeds(x, y, P_TX, f0, delta_f, k_n, T, k)

# Алгоритмы

alpha_equal_blind = equal_blind(speeds)

alpha_maximum_throughput = maximum_throughput(speeds)

alpha_proportion_fail = proportion_fair(speeds)

# Расчет метрик

sum_equal, avg_equal, min_equal = calculate_metrics(speeds, alpha_equal_blind)

total_maximum, avg_maximum, min_maximum = calculate_metrics(speeds, alpha_maximum_throughput)

total_proportion, avg_proportion, min_proportion = calculate_metrics(speeds, alpha_proportion_fail)

# Сохранение результатов

sum_equal_blind.append(sum_equal)

avg_equal_blind.append(avg_equal)

min_equal_blind.append(min_equal)

sum_maximum_throughput.append(total_maximum)

avg_maximum_throughput.append(avg_maximum)

min_maximum_throughput.append(min_maximum)

sum_proportion_fair.append(total_proportion)

avg_proportion_fair.append(avg_proportion)

min_proportion_fair.append(min_proportion)

# Усреднение результатов

results['equal_blind']['sum'].append(np.mean(sum_equal_blind))

results['equal_blind']['avg'].append(np.mean(avg_equal_blind))

results['equal_blind']['min'].append(np.mean(min_equal_blind))

results['maximum_throughput']['sum'].append(np.mean(sum_maximum_throughput))

results['maximum_throughput']['avg'].append(np.mean(avg_maximum_throughput))

results['maximum_throughput']['min'].append(np.mean(min_maximum_throughput))

results['proportion_fair']['sum'].append(np.mean(sum_proportion_fair))

results['proportion_fair']['avg'].append(np.mean(avg_proportion_fair))

results['proportion_fair']['min'].append(np.mean(min_proportion_fair))

return results

N_values = [1, 2, 4, 8, 16, 32, 64]

num_simulations = 100

results = simulate(N_values, num_simulations)

# Зависимость средней суммарной скорости от количества абонентов

plt.figure(figsize=(10, 6))

plt.plot(N_values, results['equal_blind']['sum'], label='Equal Blind', color='indigo')

plt.plot(N_values, results['maximum_throughput']['sum'], label='Maximum Throughput', color='lime')

plt.plot(N_values, results['proportion_fair']['sum'], label='Proportion Fair', color='red')

plt.title('Зависимость средней суммарной скорости от количества абонентов')

plt.xlabel('Количество абонентов (N)')

plt.ylabel('Средняя суммарная скорость (Мбит/с)')

plt.grid(True)

plt.legend()

plt.show()

# Зависимость средней скорости от количества абонентов

plt.figure(figsize=(10, 6))

plt.plot(N_values, results['equal_blind']['avg'], label='Equal Blind', color='indigo')

plt.plot(N_values, results['maximum_throughput']['avg'], label='Maximum Throughput', color='lime')

plt.plot(N_values, results['proportion_fair']['avg'], label='Proportion Fair', color='red')