Мультимедиа3

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., к.т.н., доц.				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

Изучение методов фильтрации аудиосигналов в Python. Применение рекурсивных фильтров

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: получить навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров.

Краткие теоретические сведения о задачах обработки мультимедиа аудиоконтента

В прошлой работе был изучен принцип фильтрации аудиосигналов с использованием фильтрации в спектральном пространстве. Данный метод прост, но требует большого объема вычислений, и, кроме того, характеристики фильтра будут неизменными для всей обрабатываемой записи. Фильтрацию можно производить без вычисления спектра обрабатываемого оцифрованного аудиосигнала, непосредственно во временной области. Уравнение работы рекурсивного цифрового фильтра имеет вид

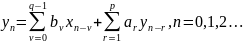, (3.1)

из данного уравнения видно, что формирование массива отсчетов выходного сигнала происходит последовательно, причем длина и входного и выходного сигнала не ограничена. Таким образом, данный способ фильтрации в равной степени пригоден как для обработки записанных аудиосигналов, так и для потокового аудио.

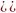
Два массива коэффициентов фильтра 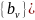полностью определяют характеристики фильтра. Все стандартные задачи фильтрации аудиоконтента в Python можно решить вызовом функций и методов, соответствующих алгоритму РЦФ, используя библиотечные функции и методы, при этом не требуется реализовывать поэлементную работу со значениями массивов аудиоданных. К уравнению (3.1) в Python прибегают только в случаях, когда хочется осуществить плавную перестройку свойств фильтра по мере обработки записи, например, чтобы создать эффект “перемещения” слушателя и/или источника звука в пространстве относительно друг друга.

Задача расчета рекурсивного фильтра заключается в выборе так называемого аналогового фильтра-прототипа некоторого порядка, и вычислении коэффициентов 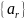и 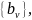при которых будет обеспечиваться желаемая частотная характеристика фильтра. Для расчета фильтров существуют разные методы, наиболее простым из которых является метод обобщенного билинейного преобразования передаточной функции аналогового фильтра-прототипа. Фильтры-прототипы бывают разных семейств (Баттерворта, Чебышева, и т. п.) и могут быть разных порядков. Чем выше порядок фильтра-прототипа, тем резче будет выражен переход от полосы пропускания к полосе подавления на частотной характеристике итогового РЦФ, но при этом увеличивается объем вычислений и возникает ряд дополнительных нюансов.

Индивидуальный вариант

Рисунок 1- Варинат задания

Ход работы

Для демонстарции работы рекурсивного фильтра, был взят линейно-частотый сигнал из лабораторной работы №2. Данный сигнал охватывает все частоты от 20 Гц до 15 кГц, что позволяет наглядно показать работу фильтра в разных частотных диапазонах. Сигнал сгенерирован исходя из формулы фазы, которая определяет как чистота сигнала изменяется во времени

,

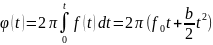где

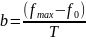
Данный ЛЧМ сигнал охватывает все частоты от начальной до конечной. Так как частота сигнала изменяется линейно во времени, сигнал является удобным для анализа и и наглядности фильтрации.

По условия задания нужно поднять уровень сигнала в диапазоне 1–3 кГц в 2 раза и подавить уровень в диапазоне 3–10 кГц в 10 раз. Заданы граничные частоты диапазонов и коэффициенты усиления и подавления. Для реализации фильтрации создаются два рекурсивных фильтра Баттерворта первого порядка (порядок фильтра установлен 1 для минимизации фазовых искажений при последующем сложении сигналов). Фильтр Баттерворта, отличается от других методов тем, что проектируется так, чтобы его амплитудно-частотная характеристика была максимально гладкой на частотах полосы пропускания.

После создания фильтров, входной сигнал пропускается через каждый из них с помощью функции signal.sosfilt. Это рекурсивная операция, которая вычисляет выходной сигнал на основе текущего и предыдущих значений входного и выходного сигналов. Выходной сигнал формируется как сумма исходного сигнала, усиленной версии сигнала после первого фильтра, ослабленной версии сигнала после второго фильтра.

Для визуализации работы фильтра построен график АЧХ, который показывает, как фильтр усиливает и ослабляет сигнал на разных частотах (Рисунок 1).

Листинг 1 –Программа создания модельного сигнала и применения рекурсивного фильтра

import numpy as np

import matplotlib.pyplot as plt

import librosa

import soundfile as sf

from scipy import signal

from scipy.signal.windows import gaussian

from scipy import signal

from scipy.signal import ShortTimeFFT

plt.close('all') # Очистка памяти

# Параметры модельного сигнала

Fd = 44100 # частота дискретизации, Гц

T = 2 # длительность сигнала, с

N = int(T * Fd)

t = np.linspace(0, T, N)

# Генерация сигнала

f0 = 20 # начальная частота

f1 = 15000 # конечная частота

phase = 2 * np.pi * t * (f0 + (f1 - f0) * t / (2 * T))

input_signal = np.sin(phase)

# Нормализация входного сигнала

Norm = np.max(np.abs(input_signal))

if Norm != 0:

input_signal = input_signal / Norm

# Параметры фильтров

order = 1 # порядок фильтра

# Граничные частоты полос пропускания фильтров

lower_frequency1, upper_frequency1 = 1000, 3000

lower_frequency2, upper_frequency2 = 3000, 10000

# Создаем фильтры

sos1 = signal.butter(order,

Wn=(lower_frequency1 / (Fd/2), upper_frequency1 / (Fd/2)),

btype='bandpass',

output='sos')

sos2 = signal.butter(order,

Wn=(lower_frequency2 / (Fd/2), upper_frequency2 / (Fd/2)),

btype='bandpass',

output='sos')

# Фильтрация сигнала

output_signal1 = signal.sosfilt(sos1, input_signal)

output_signal2 = signal.sosfilt(sos2, input_signal)

# Коэффициенты усиления и ослабления

K1 = 2.0

K2 = 0.1

# выходной сигнал

output_signal = input_signal + (K1-1)*output_signal1 + (K2-1)*output_signal2

# Расчет частотной характеристики по коэффициентам фильтра

f, H1 = signal.sosfreqz(sos1, worN=Fd, whole=False, fs=Fd)

f, H2 = signal.sosfreqz(sos2, worN=Fd, whole=False, fs=Fd)

# Комплексная частотная характеристика всего фильтра

H = 1 + (K1-1)*H1 + (K2-1)*H2

L = 20 * np.log10(np.abs(H) + 1e-10) # перевод в дБ

# График АЧХ фильтра

plt.figure(figsize=(10, 6))

plt.semilogx(f, L,color='green')

plt.title('АЧХ результирующего фильтра', fontsize=15, pad=10)

plt.xlabel('Частота [Гц]', fontsize=12)

plt.ylabel('Уровень [дБ]', fontsize=12)

plt.grid(True)

plt.axvline(1000, color='green', linestyle='--', label='1 кГц', linewidth=2)

plt.axvline(3000, color='orange', linestyle='--', label='3 кГц', linewidth=2)

plt.axvline(10000, color='purple', linestyle='--', label='10 кГц', linewidth=2)

plt.legend(fontsize=10)

plt.tight_layout()

plt.show()

# Сохранение сигналов

sf.write('C:/input_signal.wav', input_signal, Fd)

sf.write('C:/output_signal.wav', output_signal, Fd)

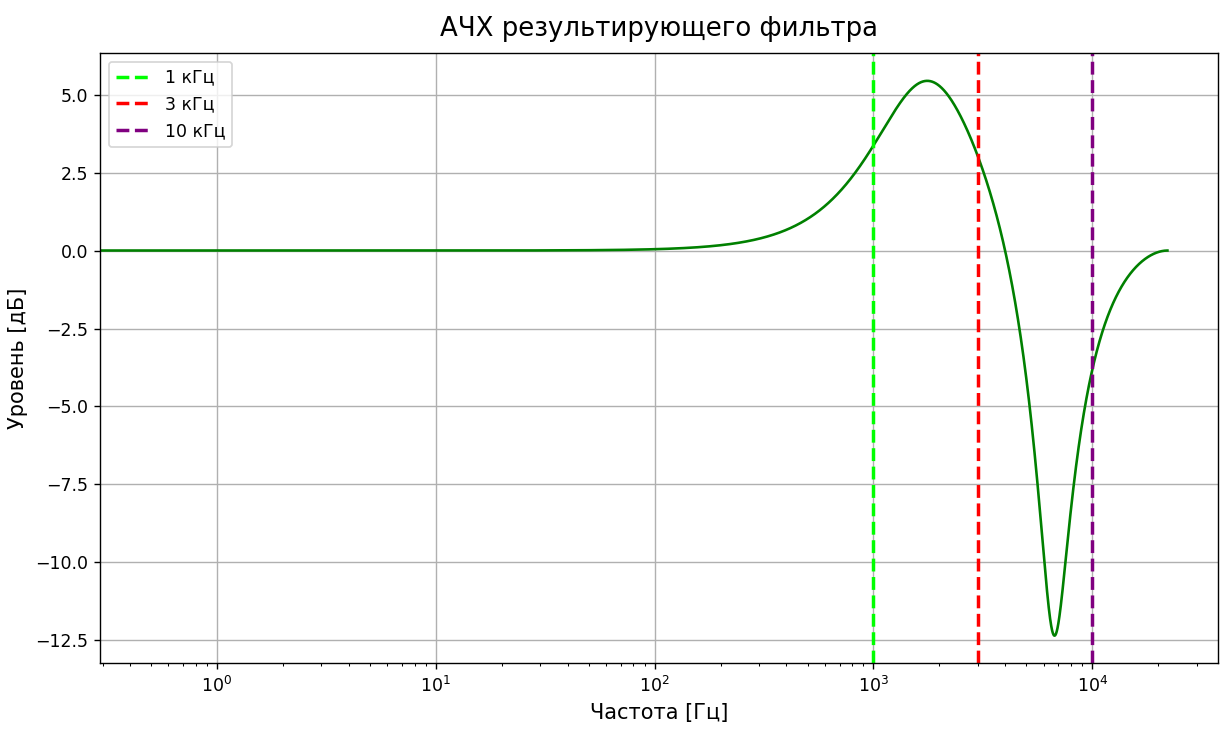
Рисунок 1- Амплитудно-частотная характеристика фильтра

На основе описания графика АЧХ результирующего фильтра, можно сказать, что фильтр оказывает плавное изменение уровня сигнала по заданным диапазонам.

Для сравнительного анализа двух типов фильтров (рекурсивного фильтра на основе фильтров Баттерворта и фильтра на основе преобразования Фурье) построены графики спектров входного и выходного сигналов, график с входным и выходным сигналом и спектограммы (Рисунок 2-7).

Листинг 2 –Программа построения графиков спектров, графиков входного и выходного сигналов и спектограмм

# Вычисляем спектр входного сигнала

Spectr_input = np.fft.fft(input_signal)

# Преобразуем в дБ:

AS_input = np.abs(Spectr_input)

eps = np.max(AS_input) * 1.0e-9

S_dB_input = 20 * np.log10(AS_input + eps)

# Вычисляем спектр выходного сигнала

Spectr_output_real = np.fft.fft(output_signal)

S_dB_output_real = 20 * np.log10(np.abs(Spectr_output_real) + eps)

f = np.arange(0, Fd/2, Fd/N) # частотная ось в Гц

S_dB_output_real = S_dB_output_real[:len(f)]

S_dB_input = S_dB_input[:len(f)]

# Вычисляем Max_dB для масштабирования

Max_A = np.max((np.max(np.abs(Spectr_input)), np.max(np.abs(Spectr_output_real))))

Max_dB = np.ceil(np.log10(Max_A)) * 20

# График спектров

plt.figure(figsize=(6, 8))

plt.semilogx(f, S_dB_input, color='b', label='Входной спектр', linewidth=1.5, alpha=0.7)

plt.semilogx(f, S_dB_output_real, color='r', label='Выходной спектр', linewidth=2.5, zorder=3)

plt.grid(True)

plt.minorticks_on()

plt.grid(True, which='major', color='#444', linewidth=1)

plt.grid(True, which='minor', color='#aaa', ls=':')

# Границы диапазонов

plt.axvline(x=1000, color='lime', linestyle='--', alpha=0.8, label='1 кГц', linewidth=2)

plt.axvline(x=3000, color='red', linestyle='--', alpha=0.8, label='3 кГц', linewidth=2)

plt.axvline(x=10000, color='purple', linestyle='--', alpha=0.8, label='10 кГц', linewidth=2)

# Оси и подписи

plt.axis([10, Fd/2, Max_dB-120, Max_dB])

plt.xlabel('Частота (Гц)', fontsize=15)

plt.ylabel('Уровень (дБ)', fontsize=15)

plt.title('Амплитудные спектры входного и выходного сигналов', fontsize=15, pad=10)

plt.legend(fontsize=13, loc='lower left')

plt.tight_layout()

plt.show()

# Графики временных сигналов

plt.figure(figsize=(8, 6))

plt.plot(t, input_signal, color='b', label='Входной сигнал', linewidth=1)

plt.plot(t, output_signal, color='r', label='Выходной сигнал', linewidth=1)

plt.xlim([0, T])

plt.xlabel('Время (с)', fontsize=10)

plt.ylabel('Амплитуда', fontsize=10)

plt.title('Графики модельного сигнала до и после фильтрации', fontsize=12, pad=10)

plt.grid(True, alpha=0.3)

plt.legend(fontsize=9)

plt.tight_layout()

plt.show()

# Спектрограммы

plt.figure(figsize=(16, 6))

# Входной сигнал

plt.subplot(1, 2, 1)

g_std = 0.3 * Fd

wind = gaussian(round(3 * g_std), std=g_std, sym=True)

SFT = ShortTimeFFT(wind, hop=round(0.25 * Fd), fs=Fd, scale_to='magnitude')

Sx_input = SFT.stft(input_signal)

# Преобразование в децибелы

epss = np.max(abs(Sx_input)) * 1e-6

Sx_db_input = 20 * np.log10(abs(Sx_input) + epss)

im1 = plt.imshow(Sx_db_input, origin='lower', aspect='auto',

extent=SFT.extent(N), cmap='viridis', vmin=-95, vmax=0)

plt.title('Спектрограмма входного сигнала', fontsize=12, pad=10)

plt.ylabel('Частота (Гц)', fontsize=10)

plt.xlabel('Время (с)', fontsize=10)

plt.semilogy()

plt.ylim([10, Fd / 2])

plt.grid(True, which='major', color='#bbbbbb', linewidth=0.5)

plt.grid(True, which='minor', color='#999999', linestyle=':', linewidth=0.5)

plt.minorticks_on()

cbar1 = plt.colorbar(im1, format='%+2.0f dB')

cbar1.set_label('Уровень (дБ)', fontsize=10)

# Выходной сигнал

plt.subplot(1, 2, 2)

Sx_output = SFT.stft(output_signal)

# Преобразование в децибелы

Sx_db_output = 20 * np.log10(abs(Sx_output) + epss)

im2 = plt.imshow(Sx_db_output, origin='lower', aspect='auto',

extent=SFT.extent(N), cmap='viridis', vmin=-95, vmax=0)

plt.title('Спектрограмма выходного сигнала', fontsize=12, pad=10)

plt.ylabel('Частота (Гц)', fontsize=10)

plt.xlabel('Время (с)', fontsize=10)

plt.semilogy()

plt.ylim([10, Fd / 2])

plt.grid(True, which='major', color='#bbbbbb', linewidth=0.5)

plt.grid(True, which='minor', color='#999999', linestyle=':', linewidth=0.5)

plt.minorticks_on()

cbar2 = plt.colorbar(im2, format='%+2.0f dB')

cbar2.set_label('Уровень (дБ)', fontsize=10)

plt.tight_layout()

plt.show()

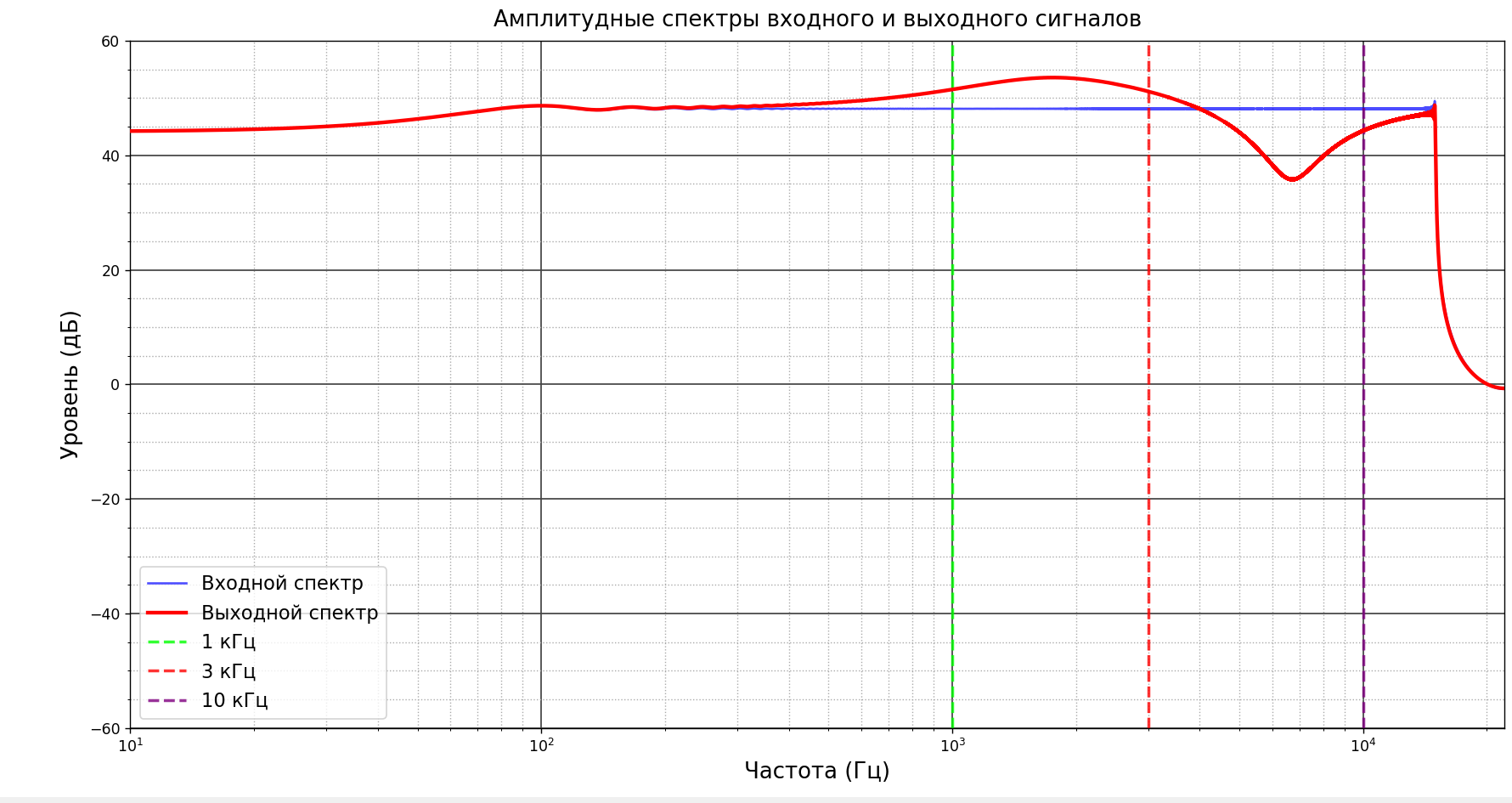
Рисунок 2- Амплитудные спектры входного и выходного сигналов после применения фильтра, реализованного методом сложения нескольких сигналов

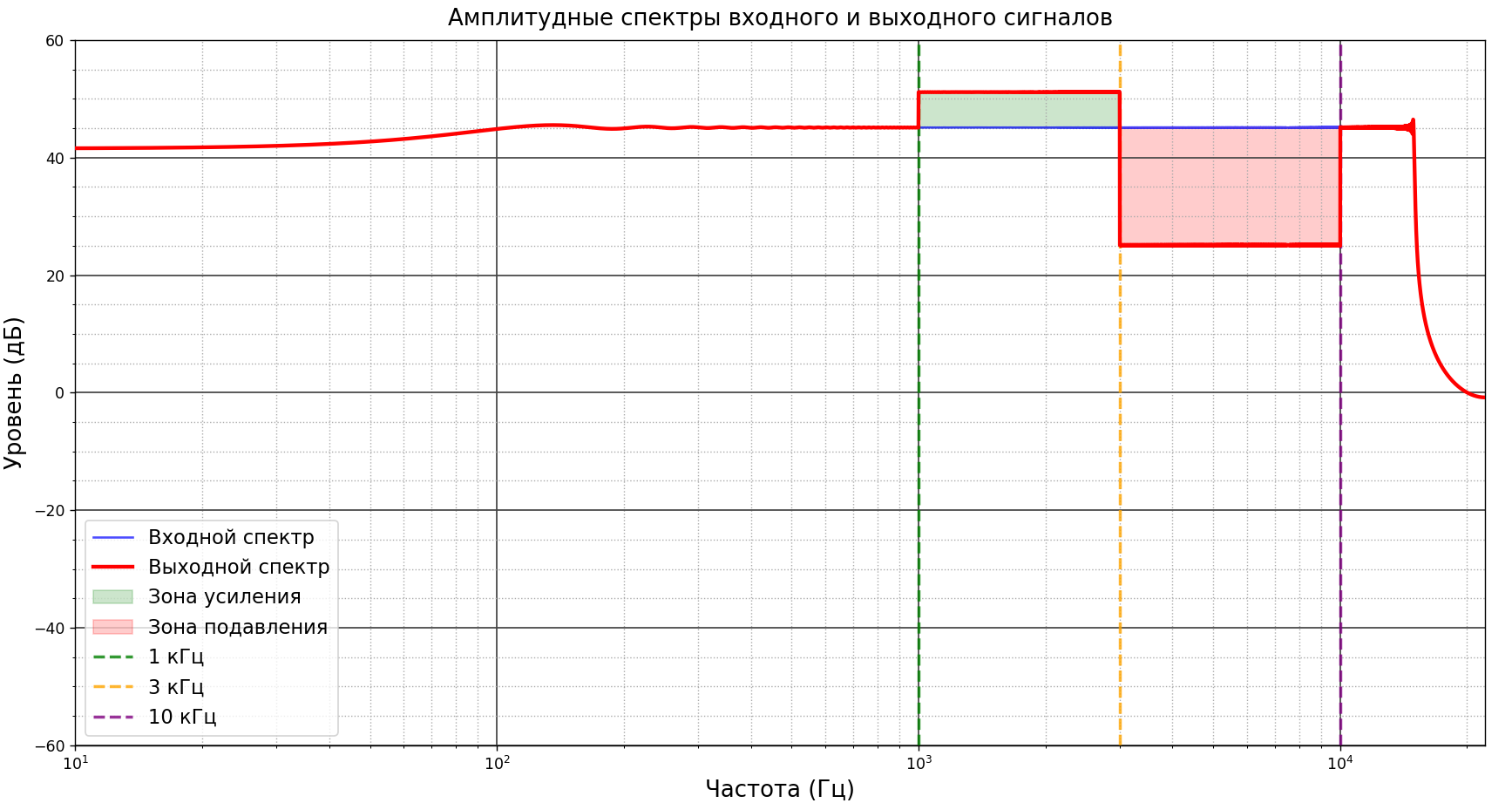
Рисунок 3- Амплитудные спектры входного и выходного сигналов после применения фильтрации в спектральном пространстве

На графике спектров для рекурсивного фильтра видно, что усиление и подавление происходят плавно, без резких переходов. На графике для Фурье фильтрации видны резкие переходы на границах зон усиления и подавления.

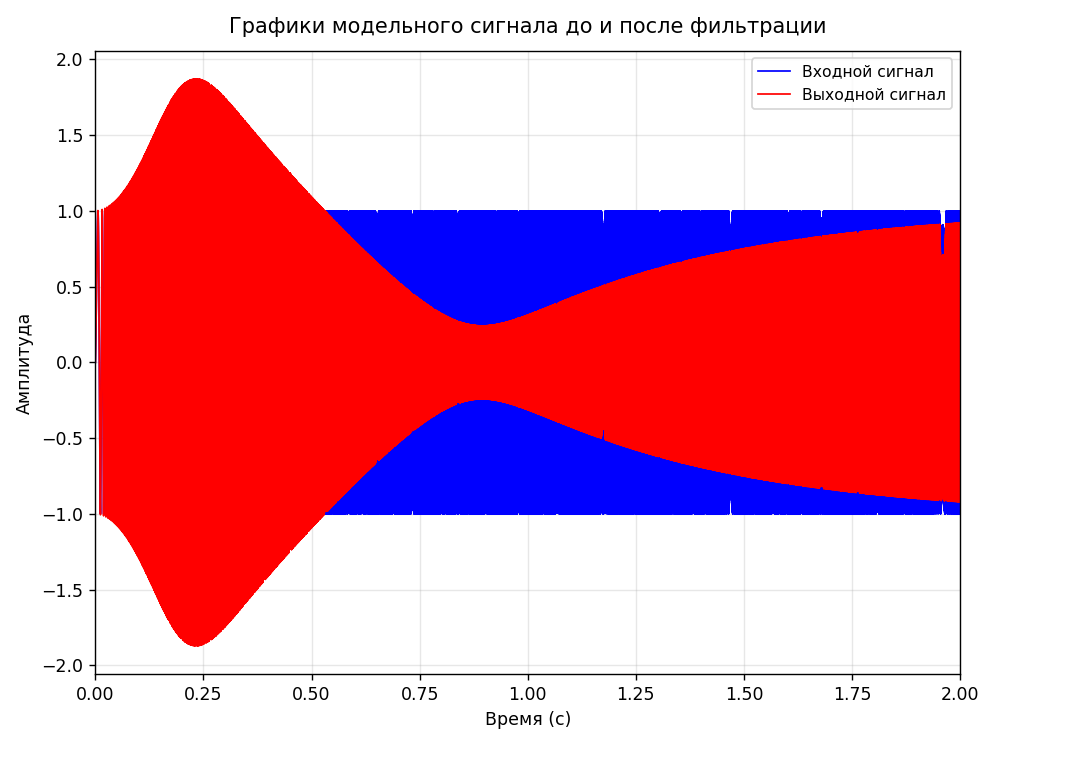
Рисунок 4- Графики модельного сигнала до и после фильтрации для рекурсивного фильтра

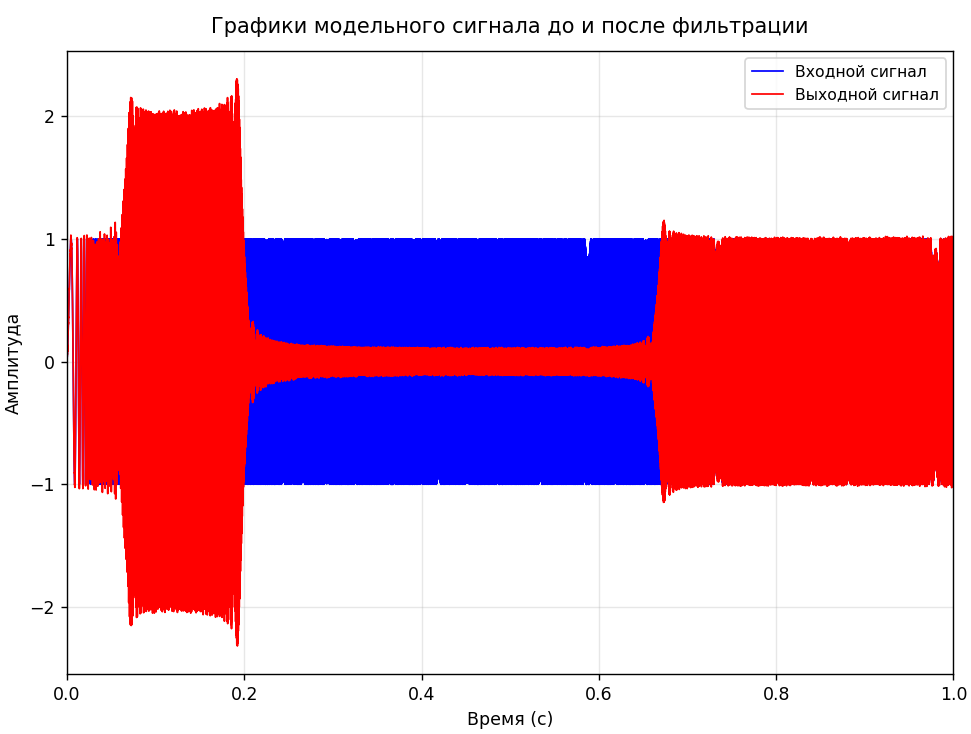
Рисунок 5- Графики модельного сигнала до и после фильтрации для фильтра в спектральном пространстве

Аналогичные выводы можно сделать по графикам сигналов до и после фильтрации, рекурсивный фильтр успешно усиливает и ослабляет сигнал в заданных диапазонах. По сравнение с Фурье-фильтрацией, усиление и ослабление происходят плавно, без резких скачков.

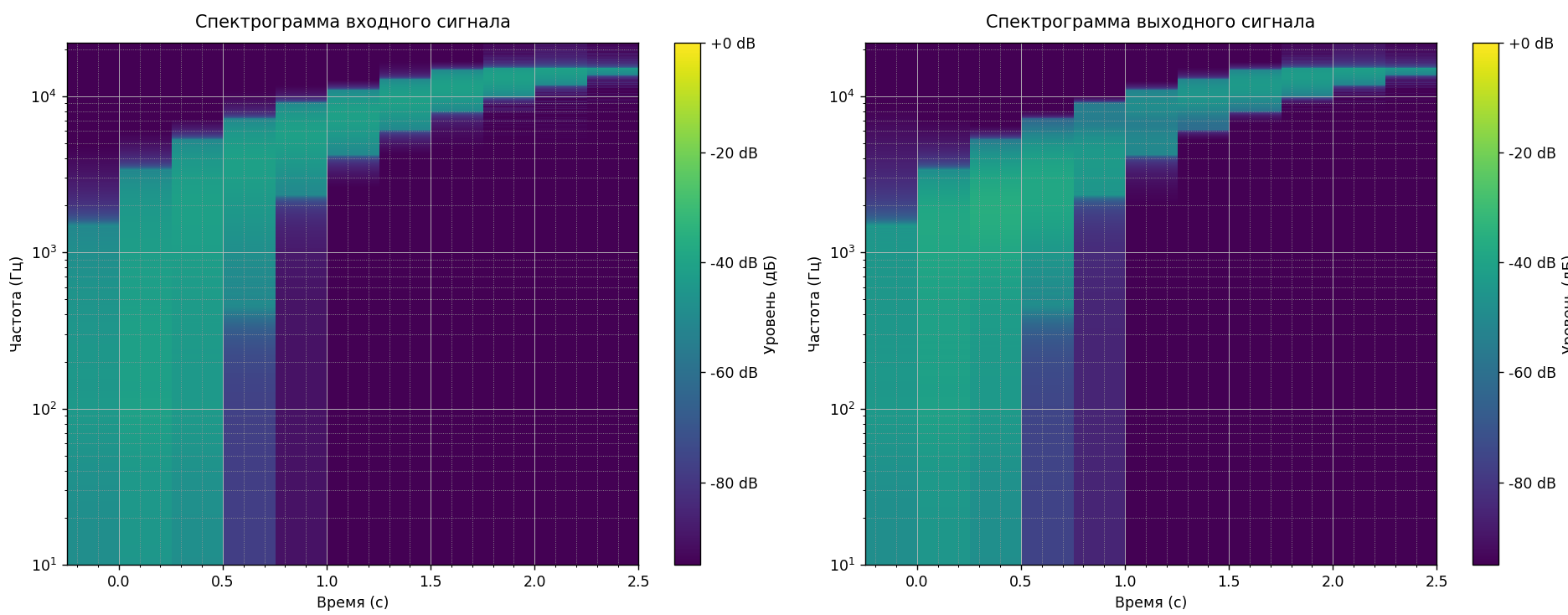
Рисунок 6- Спектограммы входного и выходного сигналов для рекурсивного фильтра

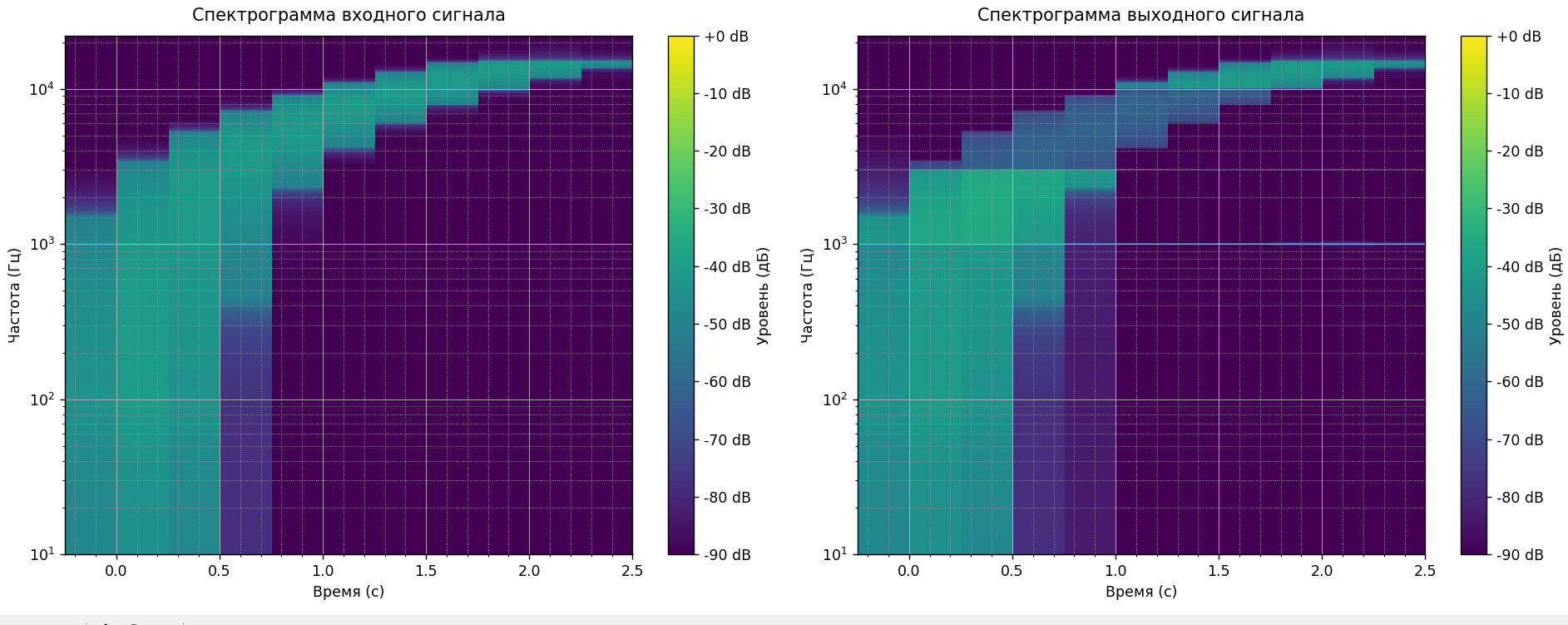
Рисунок 7- Спектограммы входного и выходного сигналов д фильтра в спектральном пространстве

По спектограммам можно сказать, что дял рекурсивного фильтра переходы между диапазонами плавные, даже, почти не заметны. Для Фурье фильтрации видны резкие переходы.

Если сравнить два выходных сигнала у двух фильтров, то можно услышать, что у выходного сигнала после применеия фильтра методом Фурье-фильтрации на фоне слышится какой-то шум, и к концу сигнала, скорее всего, из-за резкого падения частоты возникает неприятный писк. Выходной сигнал после применения рекурсивного фильтра звуков на фоне не имеет.

Как и в прошлой работе взята аудиозапись из открытой интернет-базы звуковых файлов [2]. Для того, чтобы показать как работает фильтрация на реальном аудио взята мелодия звонка старого телефона samsung. Результат работы фильтров представлен на рисунках (8-13).

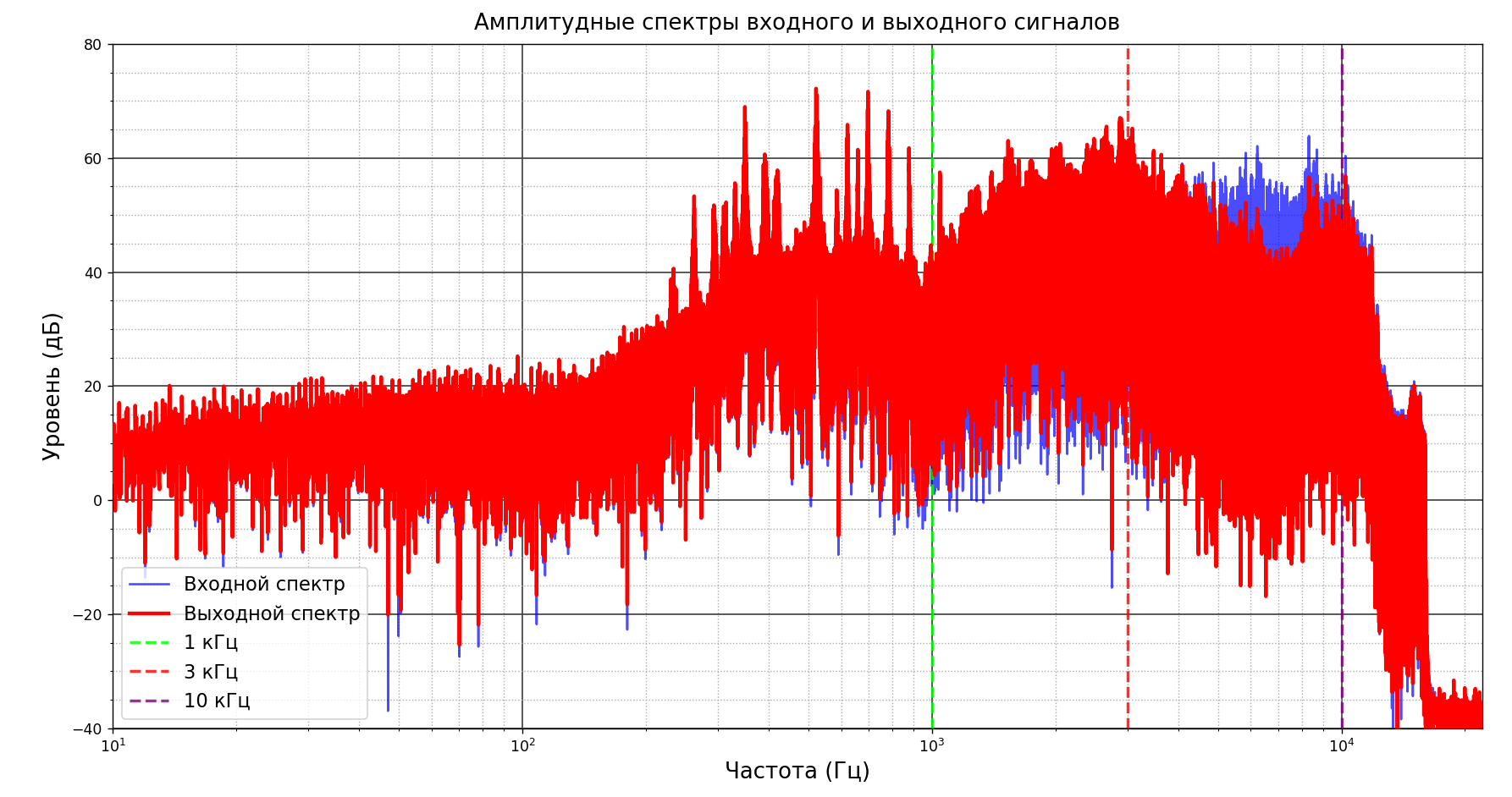
Рисунок 8- Амплитудные спектры входного и выходного сигналов после применения рекурсивного фильтра для реальногой аудиозаписи

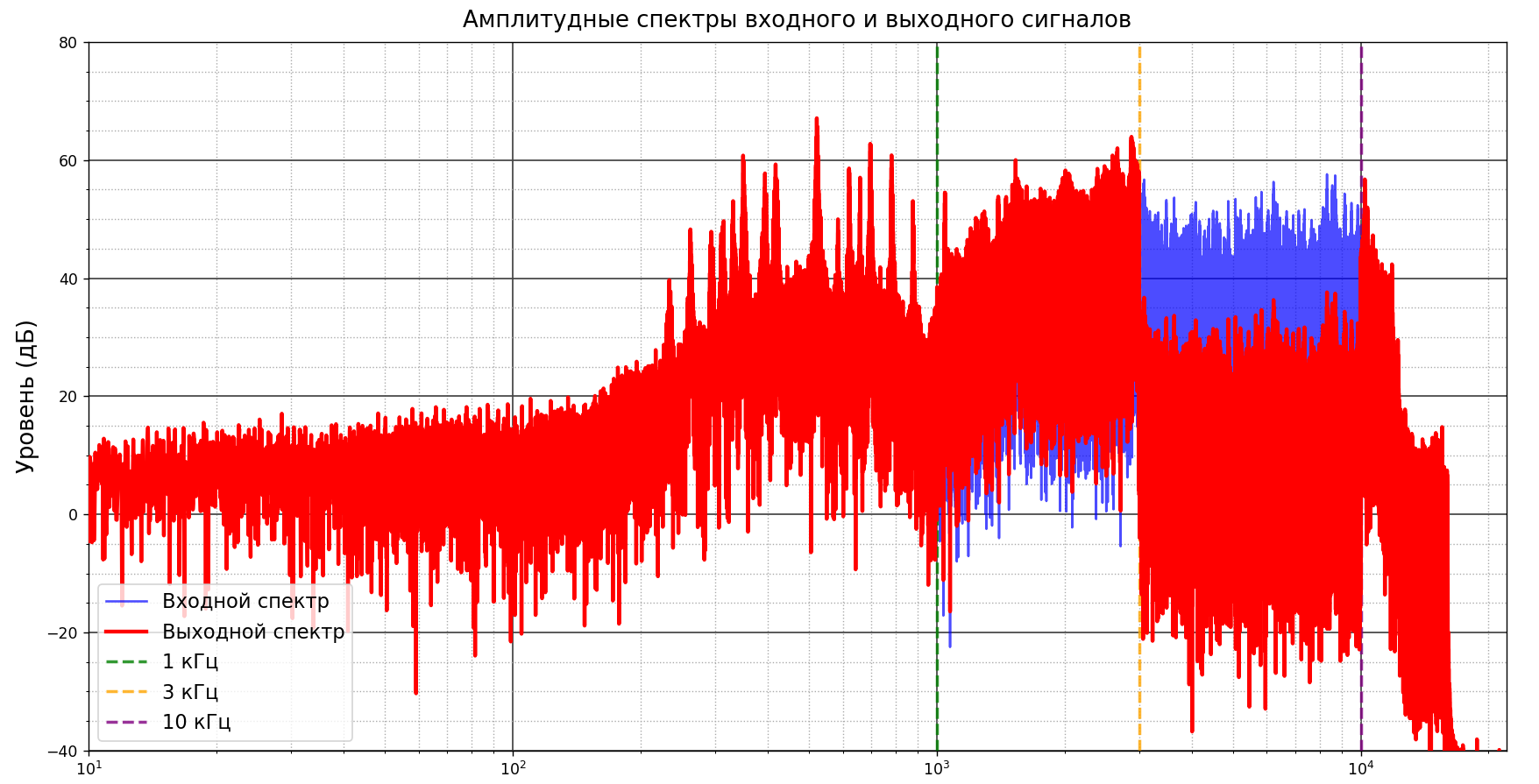
Рисунок 9- Амплитудные спектры входного и выходного сигналов после применения фильтра в спектральном пространстве для реальногой аудиозаписи

После применения фильтрации видно, что в диапазоне 1–3 кГц уровень сигнала увеличился, а в диапазоне 3–10 кГц уровень сигнала уменьшился. У фильтра на основе преобразования Фурье более наглядные изменения сигнала.

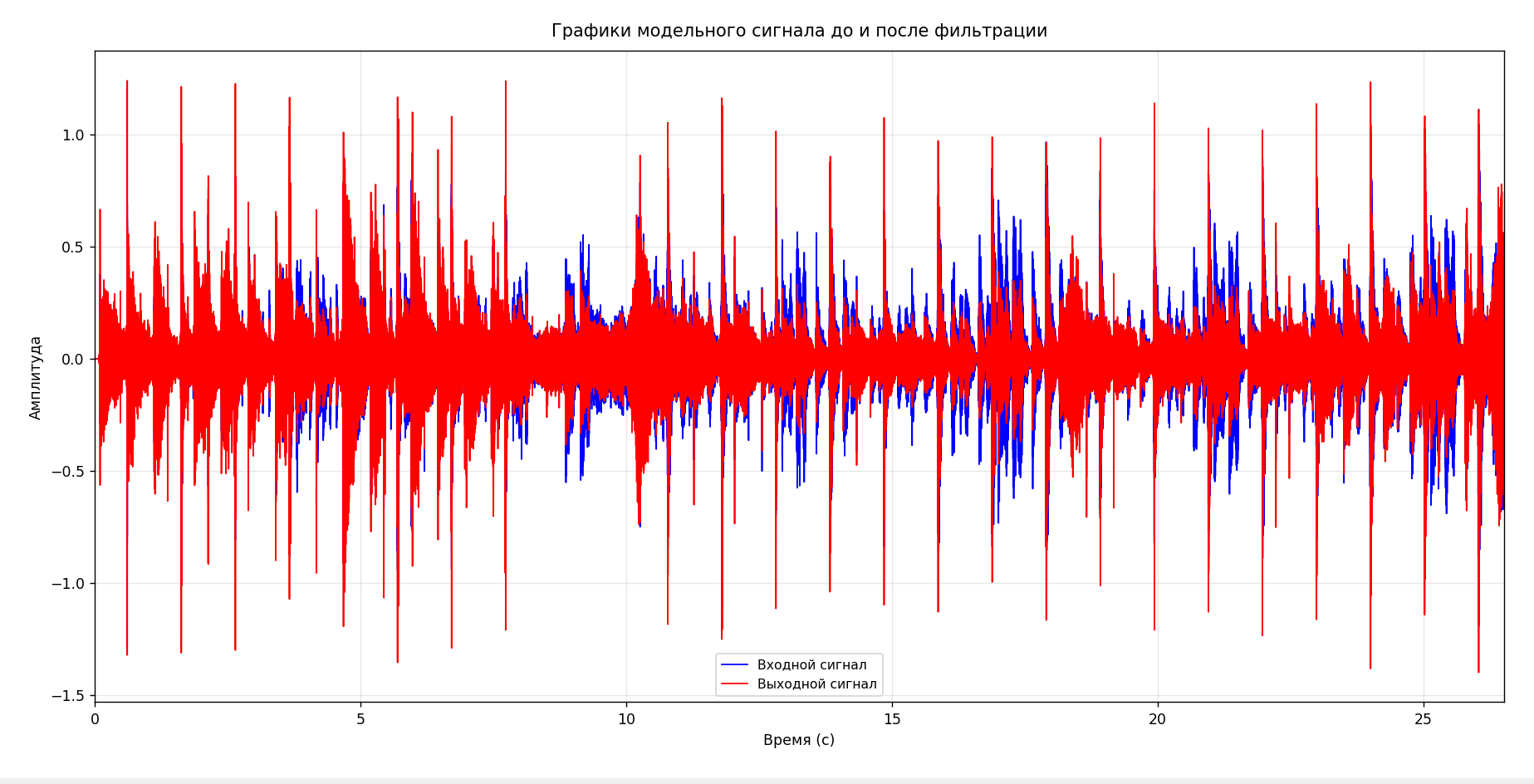
Рисунок 10- Графики сигналов до и после применения рекурсивного фильтра

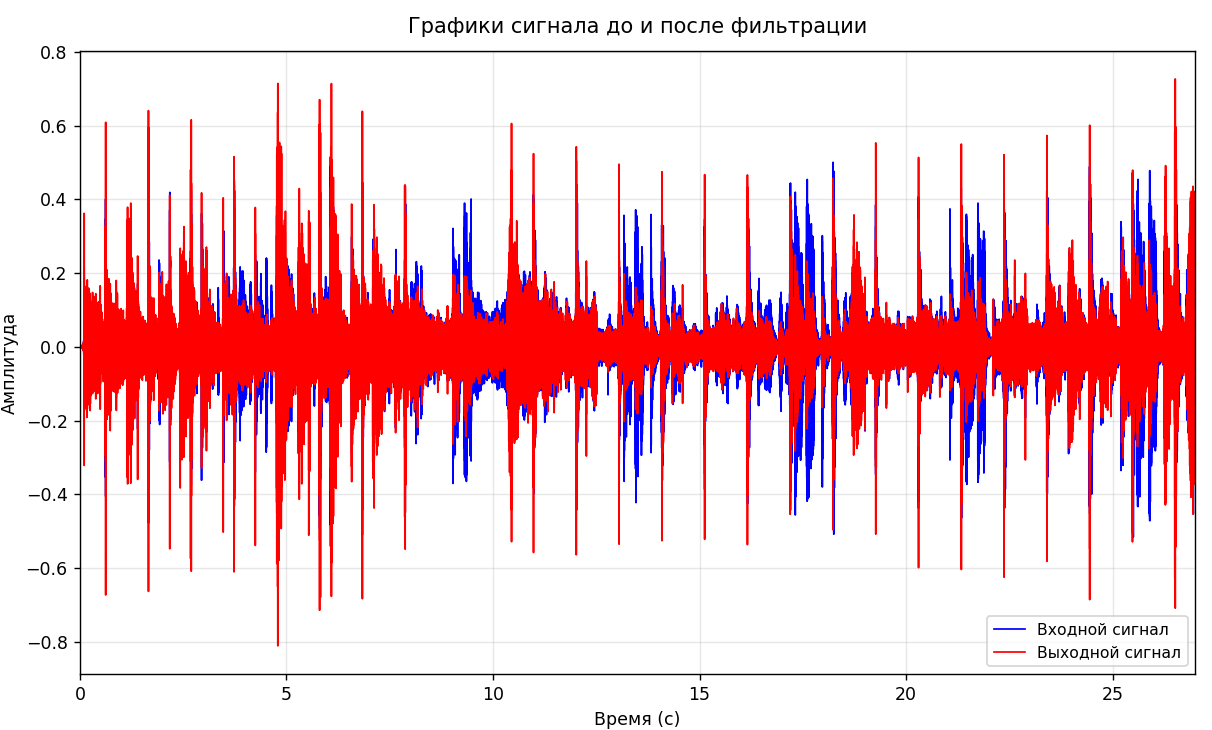
Рисунок 11- Графики реального аудиосигнала до и после применения фильтра методом Фурье-фильтрации

По графику сигналов до и после фильтрации можно сказать, что форма выходного сигнала в целом повторяет форму входного, но с некоторыми искажениями. Это может указывать на то, что фильтр, возможно, повлиял на высокочастотные или низкочастотные компоненты сигнала. У рекурсивного фильтра наименее заметные изменения сигнала, чем у фильтра на основе преобразования Фурье.

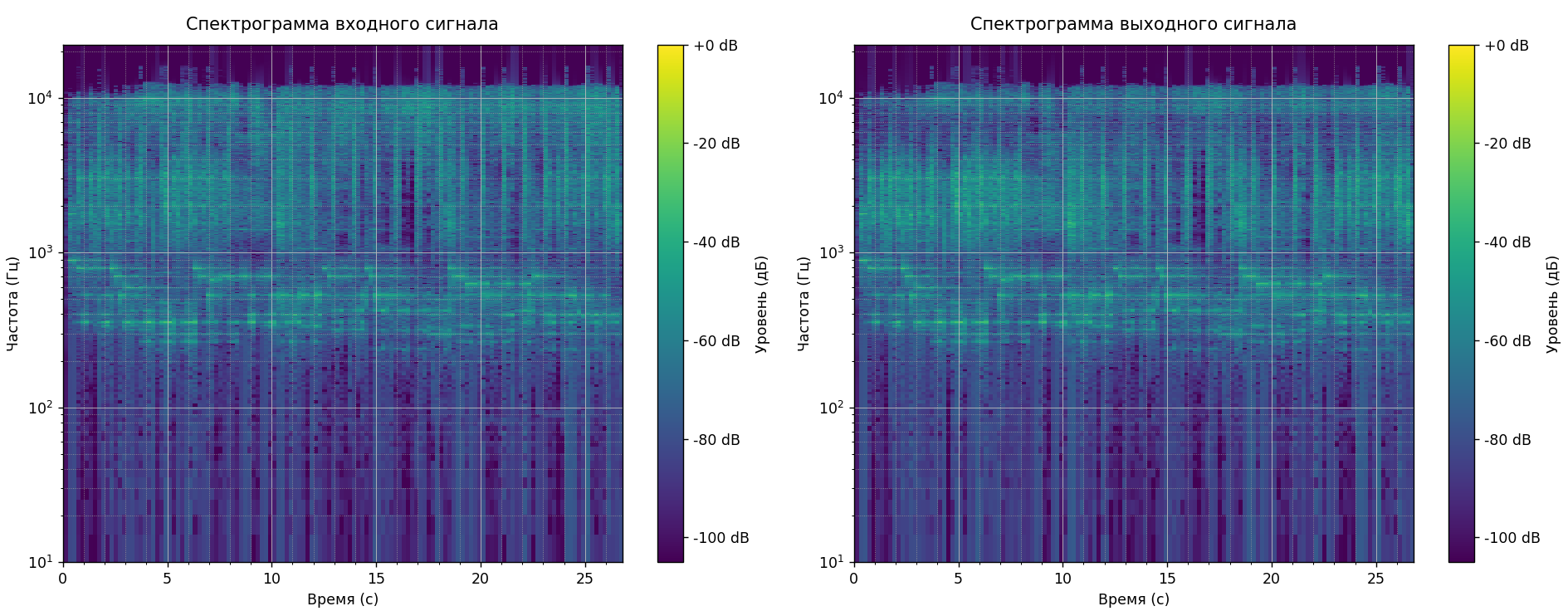
Рисунок 12- Спектограммы реального сигнала до и после применения рекурсивного фильтра

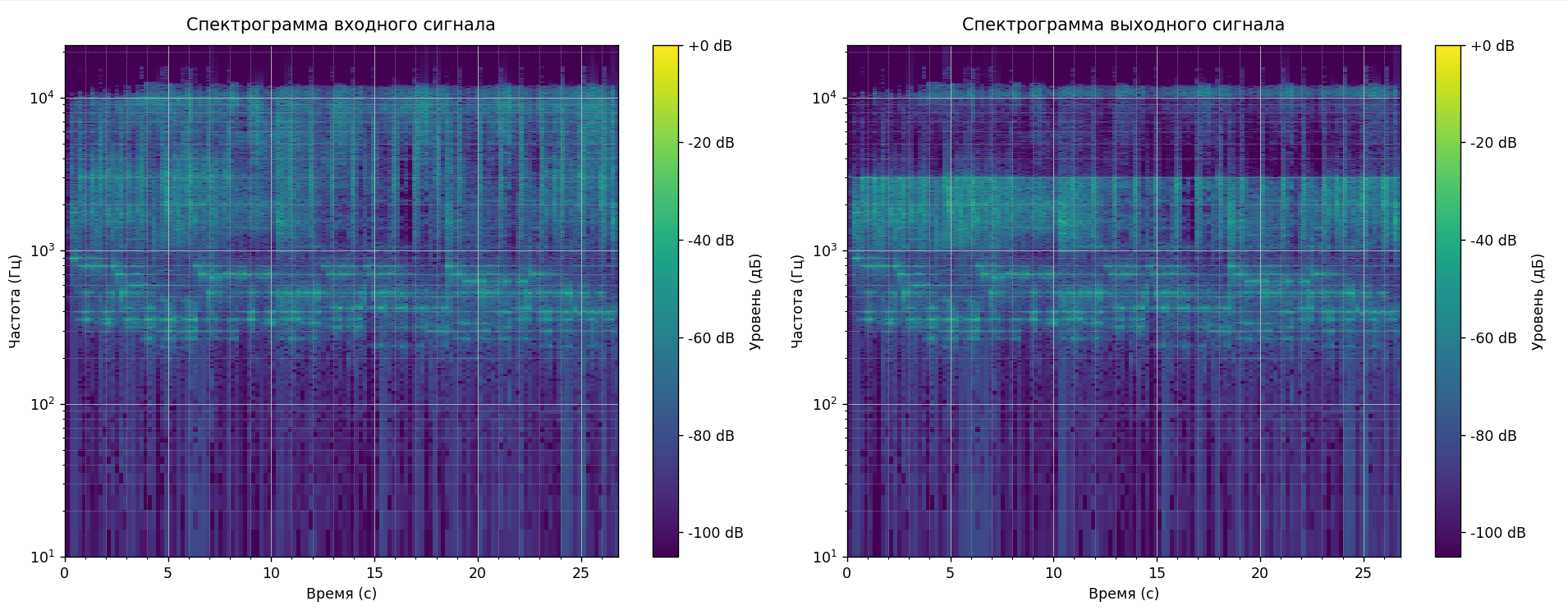
Рисунок 13- Спектограммы реального аудиосигнала до и после применения фильтра методом Фурье-фильтрации

Спектрограммы также демонстрируют плавный, почти незаметный переход между частотами у рекурсивного фильтра.

Прослушав аудио сигналов после применения фильтров, можно сказать, что после применения рекурсивного фильтра не сильно заметны изменения сигнала, аудио стало только немного тише. А вот фильтр на основе преобразования Фурье сделал сигнал более измененным, при прослушивании сигнала ощущение заложенности ушей.

Вывод

В ходе работы был реализован рекурсивный фильтр первого порядка, который применялся как к модельному ЛЧМ сигналу, так и к реальному аудиофайлу. Фильтр осуществляет усиление сигнала в 2 раза в диапазоне 1-3 кГц и ослабление в 10 раз в диапазоне 3-10 кГц. На спектрограммах и графиках четко видны результаты фильтрации. Сравнивая реализованный рекурсивный фильтр с фильтрацией на основе преобразования Фурье, можно отметить, что рекурсивный фильтр позволяет плавно изменять параметры фильтрации в процессе обработки сигнала. Также Рекурсивный фильтр сохраняет фазовые соотношения в сигнале более естественным образом, что положительно сказывается на качестве звучания обработанного аудио.

Фурье фильтрация позволяет точно задать передаточную функцию фильтра в частотной области, что может создавать артефакты на границах полос из-за резких переходов в частотной характеристике.

Список использованных источников

1. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №3 по дисциплине “Мультимедиа-технологии “. гр.4116,4117, 4118, Z0411. ГУАП, 2025. – 19 с. (Интернет-ресурс) URL: https://pro.guap.ru/inside/student/tasks/b1fa70870be81431ddf23edecfab3808/download

2. Zvukogram. База звуковых эффектов для монтажа. // URL: https://zvukogram.com/category/