Мультимедиа2

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., к.т.н., доц.				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

Основы обработки аудиосигналов средствами Python. Метод фильтрации в спектральном

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: изучить основы обработки аудиосигналов на примере метода фильтрации сигналов в спектральном пространстве.

Краткие теоретические сведения о задачах обработки мультимедиа аудиоконтента

Фильтрация является одним из широко применяемых методов обработки сигналов и аудиосигналов. К методам фильтрации часто прибегают, когда в аудиозаписи имеется несколько источников звука, и хочется подчеркнуть или ослабить звучание одного из них. Кроме того, посредством фильтрации можно достичь эффектов, имитирующих звучание, характерное для записи звука в различных замкнутых помещениях, а также, наоборот, попытаться компенсировать нежелательную неравномерность частотной характеристики примененных ранее средств записи аудиосигнала. Методологической основой фильтрации является тот факт, что любая функция может быть представлена суммой множества гармонических компонентов с различными частотами и фазами. Всевозможные аудиосигналы любой природы содержат в себе в различных сочетаниях колебания с частотами от 20 Гц до 20 кГц, причем частотные характеристики многих источников звуковых колебаний хорошо известны. Например, частотный диапазон человеческого голоса представлен последовательностью тонов, плавно сменяющих друг друга во времени, каждый из которых находится в пределах границ между самым низким и самым высоким звуками: обычно от 64 до 1400 Гц.

Электронные синтезаторы позволяют формировать звуки в любом сочетании отдельных частотных составляющих. Компоненты человеческого голоса можно условно разделить на три диапазона, согласно входящим в них звукам: взрывным, гласным и шипящим. Взрывные звуки лежат в диапазоне от 125 Гц до 250 Гц и "отвечают" за разборчивость речи, так как именно они позволяют нам определить, кто именно говорит. На долю гласных, которые лежат в диапазоне от 350 Гц до 2000 Гц, приходится максимальное количество голосовой энергии. Шипящие в диапазоне от 1500 Гц до 4000 Гц несут сравнительно мало энергии, однако от них зависит четкость и разборчивость речи. Частотный диапазон от 63 Гц до 500 Гц содержит около 60% всей энергии голоса, однако на его долю приходится лишь 5% информационного наполнения речи. Диапазон от 500 Гц до 1 кГц содержит около 35% информации, а остальные 60% информационного наполнения приходятся на долю "шипящего" диапазона от 1 кГц до 8 кГц, который несет лишь 5% энергии.

Для получения информации о частотном составе любых сигналов в дискретном времени существует специальный метод и алгоритм – быстрое преобразование Фурье (БПФ). В результате его применения к массиву 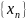, который представляет собой, например, последовательность оцифрованных значений звука, образуется массив значений спектра 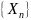. Значения спектра являются комплексными числами, а модуль каждого из них пропорционален амплитуде гармонического компонента, содержащегося в обрабатываемой записи аудисосигнала. Связь целочисленного индекса элементов массива . с частотой дается формулой

,

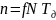где 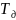– период дискретизации сигнала.

Существует также и алгоритм обратного действия (обратное БПФ): по массиву значений спектра можно вычислить массив значений сигнала . Идея метода фильтрации в спектральном пространстве (который также известен под названием “метод Фурье-фильтрации”) заключается в том, чтобы каким-то образом изменить спектр исходного сигнала и восстановить аудиосигнал из измененного спектра.

Таким образом, метод фильтрации реализуется в три шага:

1) производится вычисление спектра исходного аудиосигнала ,

2) осуществляется изменение некоторого количества значений спектра в соответствии желаемыми частотными свойствами фильтра, в результате чего получается измененный спектр

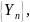
3) выполняется формировании выходного аудиосигнала посредством вычисления обратного преобразования Фурье спектра .

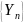Процедура изменения спектра исходного сигнала при реализации методов линейной фильтрации реализуется как поэлементное умножение двух массивов: исходного спектра и предварительно сформированного массива значений передаточной функции фильтра :

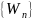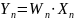, для

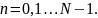
При задании массива исходят из требований к типу фильтрации. Например, если необходимо оставить без изменения частотные компоненты аудиосигнала в определенном диапазоне частот и максимально ослабить остальные компоненты, то используется следующий подход:

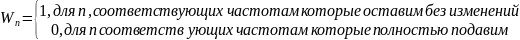
При реализации цифровых эквалайзеров можно задавать желаемый коэффициент пропускания, отличный от нуля, для разных частотных диапазонов, можно также задавать функциональную зависимость желаемого коэффициента пропускания от частоты.

Индивидуальный вариант

Рисунок 1- Варинат задания

Ход работы

Для демонстарции работы фильтра, был создан линейно-частотый сигнал, который охватывает все частоты от 20 Гц до 15 кГц, что позволяет наглядно показать работу фильтра в разных частотных диапазонах. Сигнал сгенерирован исходя из формулы фазы, которая определяет как чистота сигнала изменяется во времени

,

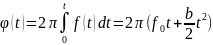где

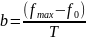
Данный ЛЧМ сигнал охватывает все частоты от начальной до конечной. Так как частота сигнала изменяется линейно во времени, сигнал является удобным для анализа и и наглядности фильтрации.

Чтобы поднять уровень сигнала в диапазоне 1–3 кГц в 2 раза и подавить уровень в диапазоне 3–10 кГц в 10 раз, используется частотная фильтрация. Заданы граничные частоты диапазонов и коэффициенты усиления и подавления. Модельный сигнал преобразуется из временной области в частотную, т.е. преобразуется в спектр с помощью быстрого преобразования Фурье. Для того, чтобы задать диапазоны фильтрации, частоты переведены в индексы массива.

Далее создается массив из единиц W, который определяет, как фильтр изменяет амплитуды частотных компонент. В тех диапазонах, где нужно амплитуды увеличиваются или уменьшаются, остальные частоты остаются без изменений. Зеркальные диапазоны задаются для учёта отрицательных частот.

Для применения фильтра спектр входного сигнала умножается на передаточную функцию фильтра. После применения фильтра спектр преобразуется обратно во временную область с помощью обратного БПФ.

Листинг 1 –Программа создания модельного сигнала и применения фильтрации

import numpy as np

import matplotlib.pyplot as plt

import librosa

import soundfile as sf

import librosa.display

from scipy.signal import windows

from scipy.signal.windows import gaussian

from scipy.signal import ShortTimeFFT

plt.close('all') # Очистка памяти

# Параметры модельного сигнала

Fd = 44100 # частота дискретизации, Гц

T = 2 # длительность сигнала, с

N = int(T * Fd)

t = np.linspace(0, T, N)

f0 = 20 # начальная частота

f1 = 15000 # конечная частота

phase = 2 * np.pi * t * (f0 + (f1 - f0) * t / (2 * T))

input_signal = np.sin(phase)

Norm = np.max(np.abs(input_signal))

if Norm != 0:

input_signal = input_signal / Norm

# Вычисляем спектр входного сигнала

Spectr_input = np.fft.fft(input_signal)

# Преобразуем в дБ:

AS_input = np.abs(Spectr_input)

eps = np.max(AS_input) * 1.0e-9

S_dB_input = 20 * np.log10(AS_input + eps)

# Задаем граничные частоты полос фильтра

f1, f2, f3 = 1000, 3000, 10000 # частоты в Гц

k1, k2 = 2.0, 0.1 # усиление в 2 раза и подавление в 10 раз

# Переводим Герцы в целочисленные индексы массива:

n1 = round(N * f1 / Fd)

n2 = round(N * f2 / Fd)

n3 = round(N * f3 / Fd)

# Создаем массив значений передаточной функции фильтра

W = np.ones_like(Spectr_input) # массив из единиц

W[n1:n2 + 1] = k1 # усиление в диапазоне 1-3 кГц

W[n2:n3 + 1] = k2 # подавление в диапазоне 3-10 кГц

W[N - n3:N - n2 + 1] = k2 # зеркальное подавление

W[N - n2:N - n1 + 1] = k1 # зеркальное усиление

# Считаем массив значений спектра для выходного сигнала

Spectr_output = Spectr_input * W

#отношение i/r=max(|im(S)|)/ real(|im(S)|):

print(np.max(np.abs(np.imag(np.fft.ifft(Spectr_output))))/np.max(np.abs(np.real(np.fft.ifft(Spectr_output)))))

# Обратное БПФ от модифицированного спектра

output_signal = np.real(np.fft.ifft(Spectr_output))

# Сохранение входного сигнала в файл

sf.write('input_signal.wav', input_signal, Fd)

# Сохранение выходного сигнала в файл

sf.write('output_signal.wav', output_signal, Fd)

# Сравниваем спектры до и после фильтрации

f = np.arange(0, Fd / 2, Fd / N) # Перевести Абсциссу в Гц

S_dB_output = 20 * np.log10(np.abs(np.fft.fft(output_signal))[:len(f)] + eps)

S_dB_input = S_dB_input[:len(f)]

# Вычисляем Max_dB для масштабирования

Max_A = np.max((np.max(np.abs(Spectr_input)), np.max(np.abs(Spectr_output))))

Max_dB = np.ceil(np.log10(Max_A)) * 20

Затем для визуализации примененного фильтра построены графики спектров входного сигнала и выходного сигнала после фильтрации (Рисунок 1). Также построены график с входным и выходным сигналом и спектограммы сигналов до и после фильтрации (Рисунок 2-3)

Листинг 2 –Программа построения графиков спектров, графиков входного и выходного сигналов и спектограмм

# График спектров

plt.figure(figsize=(6, 8))

plt.semilogx(f, S_dB_input, color='b', label='Входной спектр', linewidth=1.5, alpha=0.7)

plt.semilogx(f, S_dB_output, color='r', label='Выходной спектр', linewidth=2.5, zorder=3)

plt.grid(True)

plt.minorticks_on() # отобразит мелкую сетку на лог.масштабе

plt.grid(True, which='major', color = '#444', linewidth = 1)

plt.grid(True, which='minor', color='#aaa', ls=':')

# Заливка между графиками для подчеркивания разницы

plt.fill_between(f, S_dB_input, S_dB_output, where=(f >= f1) & (f <= f2),

color='g', alpha=0.2, label='Зона усиления')

plt.fill_between(f, S_dB_input, S_dB_output, where=(f >= f2) & (f <= f3),

color='r', alpha=0.2, label='Зона подавления')

# Границы диапазонов

plt.axvline(x=f1, color='g', linestyle='--', alpha=0.8, label='1 кГц', linewidth=2)

plt.axvline(x=f2, color='orange', linestyle='--', alpha=0.8, label='3 кГц', linewidth=2)

plt.axvline(x=f3, color='purple', linestyle='--', alpha=0.8, label='10 кГц', linewidth=2)

# Оси и подписи

plt.axis([10, Fd / 2, Max_dB - 120, Max_dB])

plt.xlabel('Частота (Гц)', fontsize=15 )

plt.ylabel('Уровень (дБ)', fontsize=15)

plt.title('Амплитудные спектры входного и выходного сигналов', fontsize=15, pad=10)

plt.legend(fontsize=13, loc='lower left')

plt.tight_layout()

# Графики временных сигналов

plt.figure(figsize=(8, 6))

plt.plot(t, input_signal, color='b', label='Входной сигнал', linewidth=1)

plt.plot(t, output_signal, color='r', label='Выходной сигнал', linewidth=1)

plt.xlim([0, T])

plt.xlabel('Время (с)', fontsize=10)

plt.ylabel('Амплитуда', fontsize=10)

plt.title(' Графики модельного сигнала до и после фильтрации', fontsize=12, pad=10)

plt.grid(True, alpha=0.3)

plt.legend(fontsize=9)

plt.tight_layout()

# Спектрограммы

plt.figure(figsize=(16, 6))

# Входной сигнал

plt.subplot(1, 2, 1)

g_std = 0.2 * Fd

wind = gaussian(round(2 * g_std), std=g_std, sym=True)

SFT = ShortTimeFFT(wind, hop=round(0.1 * Fd), fs=Fd, scale_to='magnitude')

Sx_input = SFT.stft(input_signal)

# Преобразование в децибелы

epss = np.max(abs(Sx_input)) * 1e-6

Sx_db_input = 20 * np.log10(abs(Sx_input) + epss)

im1 = plt.imshow(Sx_db_input, origin='lower', aspect='auto',

extent=SFT.extent(N), cmap='viridis', vmin=-88, vmax=0)

plt.title('Спектрограмма входного сигнала', fontsize=12, pad=10)

plt.ylabel('Частота (Гц)', fontsize=10)

plt.xlabel('Время (с)', fontsize=10)

plt.semilogy()

plt.ylim([10, Fd / 2])

plt.grid(True, which='major', color='#bbbbbb', linewidth=0.5)

plt.grid(True, which='minor', color='#999999', linestyle=':', linewidth=0.5)

plt.minorticks_on()

cbar1 = plt.colorbar(im1, format='%+2.0f dB')

cbar1.set_label('Уровень (дБ)', fontsize=10)

# Выходной сигнал

plt.subplot(1, 2, 2)

Sx_output = SFT.stft(output_signal)

# Преобразование в децибелы

Sx_db_output = 20 * np.log10(abs(Sx_output) + epss)

im2 = plt.imshow(Sx_db_output, origin='lower', aspect='auto',

extent=SFT.extent(N), cmap='viridis', vmin=-88, vmax=0)

plt.title('Спектрограмма выходного сигнала', fontsize=12, pad=10)

plt.ylabel('Частота (Гц)', fontsize=10)

plt.xlabel('Время (с)', fontsize=10)

plt.semilogy()

plt.ylim([10, Fd / 2])

plt.grid(True, which='major', color='#bbbbbb', linewidth=0.5)

plt.grid(True, which='minor', color='#999999', linestyle=':', linewidth=0.5)

plt.minorticks_on()

cbar2 = plt.colorbar(im2, format='%+2.0f dB')

cbar2.set_label('Уровень (дБ)', fontsize=10)

plt.tight_layout()

plt.show()

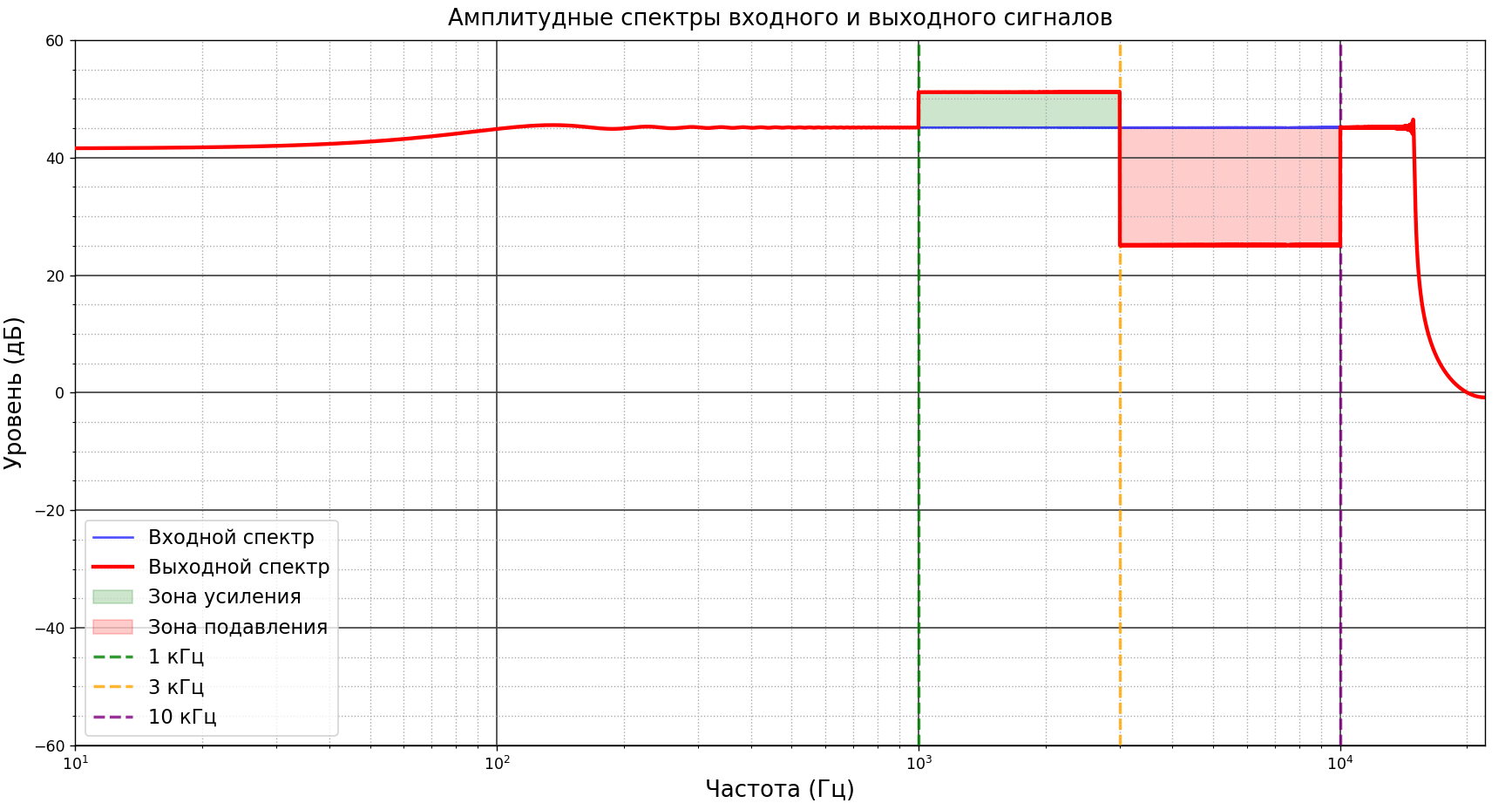
Рисунок 1- Амплитудные спектры входного и выходного сигналов

На спектре выходного сигнала явно видны зоны усиления и подавления. В зоне усиления 1 кГц - 3 кГц уровень сигнала увеличился в 2 раза (примерно 6 дБ), что соответствует коэффициенту усиления. В зоне подавления 3 кГц - 10 кГц уровень сигнала уменьшился в 10 раз (примерно 20 дБ). Границы диапазонов четко выделены на графике, что подтверждает корректность работы фильтра.

Рисунок 2- Графики модельного сигнала до и после фильтрации

На графике модельных сигналов видно,что после фильтрации амплитуда сигнала изменяется в зависимости от частоты. По заданным параметрам фидльтра наблюдаетмя как усиление, так и подавление сигнала.

Рисунок 3- Спектограммы входного и выходного сигналов

На спектрограмме выходного сигнала явно видны изменения в интенсивности сигнала. В диапазоне от 1 кГц до 3 кГц уровень дб увеличился.В диапазоне от 3 кГц до 10 кГц уровень дб значительно снизился.Спектрограмма подтверждает, что фильтр корректно обработал сигнал, усиливая и подавляя заданные частотные диапазон.

Затем была взята аудиозапись из открытой интернет-базы звуковых файлов [2]. Для того, чтобы показать как работает фильтрация на реальном аудио взята мелодия звонка старого телефона samsung. Результат работы фильтра представлен на рисунках 4-6.

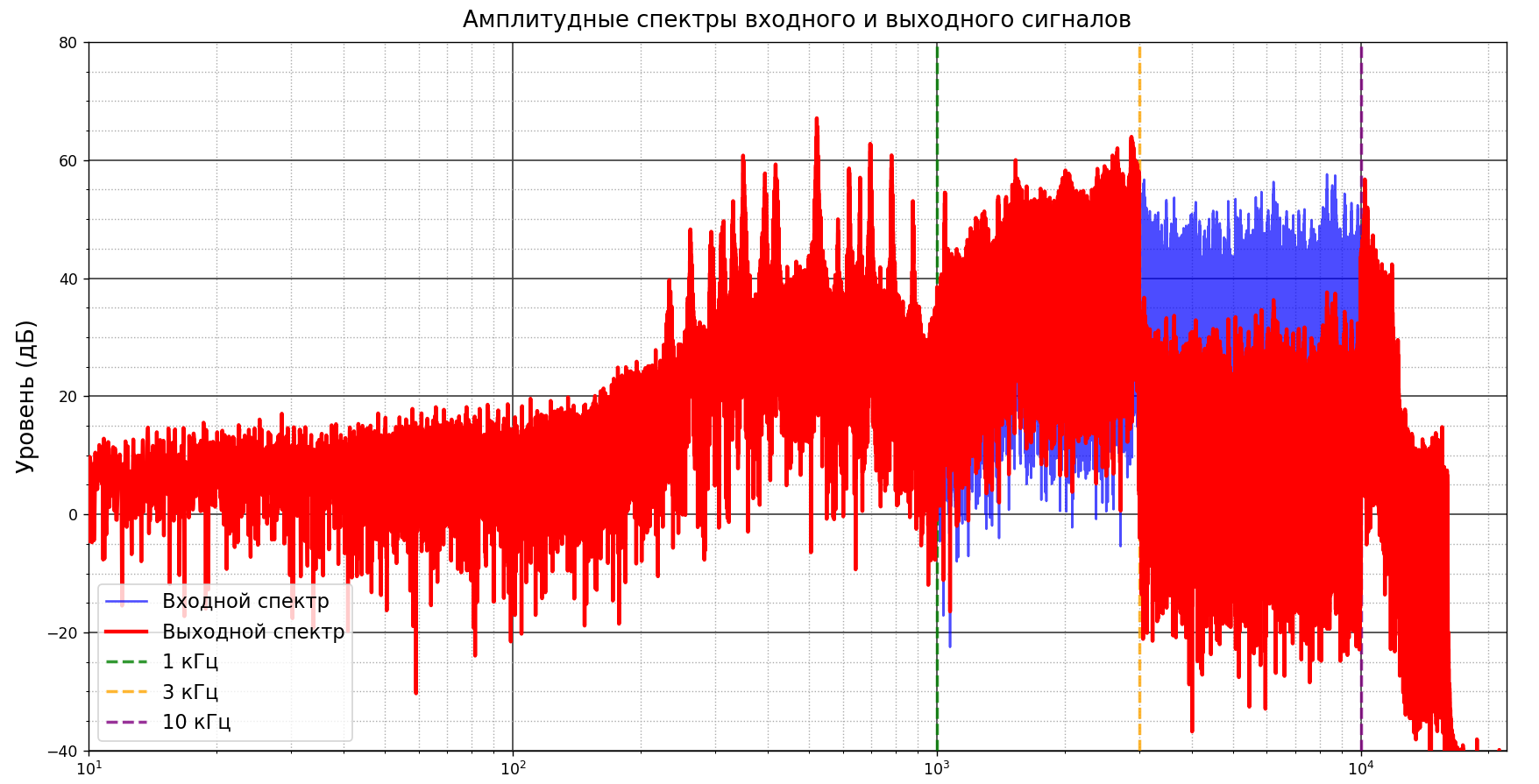
Рисунок 4- Амплитудные спектры входного и выходного сигналов для реальногой аудиозаписи

После применения фильтрации видно, что в диапазоне 1–3 кГц уровень сигнала увеличился, а в диапазоне 3–10 кГц уровень сигнала уменьшился, что соответствует заданным параметрам фильтра.

Рисунок 5- Графики реального аудиосигнала до и после фильтрации

По графику сигналов до и после фильтрации можно сказать, что форма выходного сигнала в целом повторяет форму входного, но с некоторыми искажениями. Это может указывать на то, что фильтр, возможно, повлиял на высокочастотные или низкочастотные компоненты сигнала.

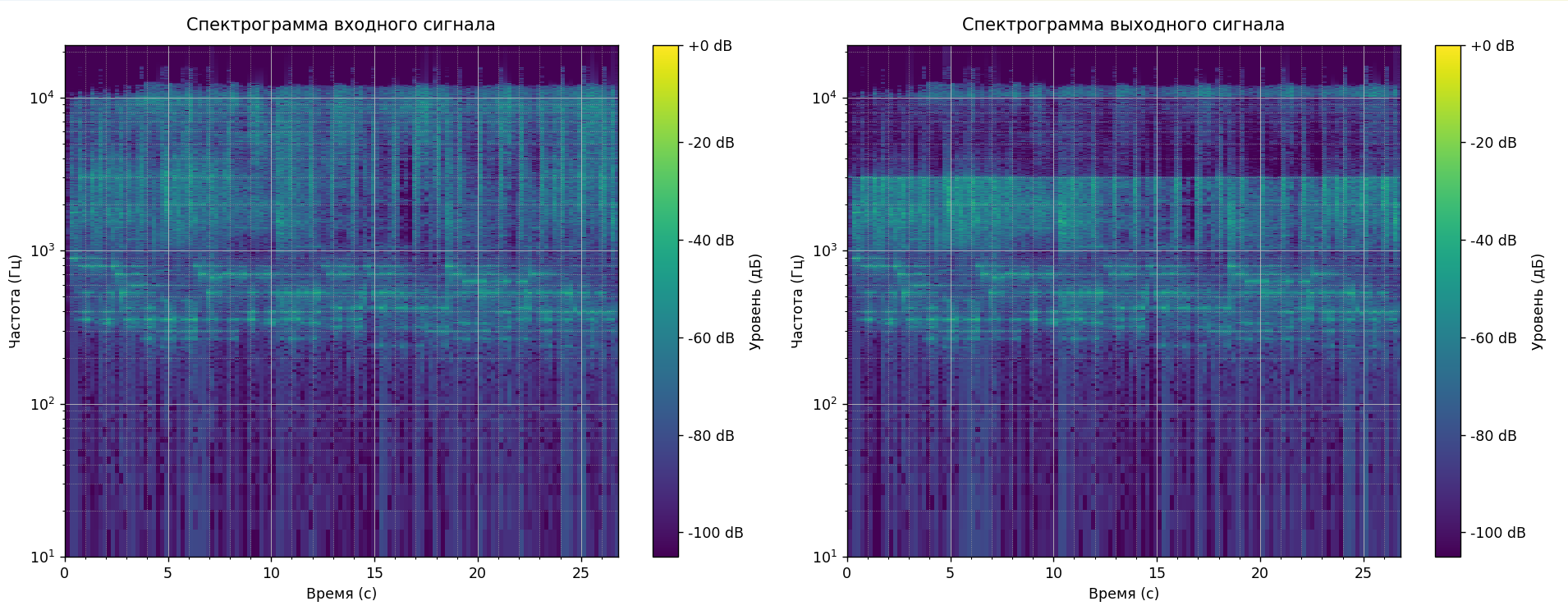
Рисунок 6- Спектограммы входного и выходного аудиосигналов

Спектрограммы также демонстрируют, что фильтр успешно подавил высокие частоты и усилил средние частоты, что соответствует заданным параметрам.

Вывод

В ходе работы был успешно реализован частотный фильтр, который усиливает сигнал в диапазоне 1–3 кГц в 2 раза и подавляет сигнал в диапазоне 3–10 кГц в 10 раз. На модельном линейно-частотном сигнале и реальной аудиозаписи продемонстрирована корректная работа фильтра. Амплитудные спектры, графики сигналов и спектрограммы подтвердили, что фильтр эффективно усиливает и подавляет заданные частотные диапазоны. Результаты визуализации наглядно показывают изменения в уровнях сигнала, что соответствует ожидаемым параметрам фильтра.

Список использованных источников

1. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №2 по дисциплине “Мультимедиа-технологии “. гр.4116,4117, 4118, Z0411. ГУАП, 2025. – 19 с. (Интернет-ресурс) URL: https://pro.guap.ru/inside/student/tasks/a575524e172cc332ea52af045874774a/download

2. Zvukogram. База звуковых эффектов для монтажа. // URL: https://zvukogram.com/category/