Мультимедиа1

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., к.т.н., доц.				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

Основы моделирования и обработки аудиосигналов средствами Python

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: получить представление о принципах формирования аудиосигналов и приобрести навыки обработки звуковых файлов с использованием средств Python.

Краткие теоретические сведения о задачах обработки мультимедиа аудиоконтента

Аудиоконтент является одной из составляющих мультимедиа. Оцифрованный звук сохраняется в файлах, данные в которых представлены в стандартных форматах, таких как *.wav, *.mp3, *.ogg. Самые популярные библиотеками для работы со звуковыми файлами в Python – это PyWave, Pyaudio, Librosa и soundfile. У каждой из библиотек есть свой набор инструментов для работы с аудио и особенности практического использования. Библиотеку Librosa, часто используют для продвинутого анализа аудиосигнала и soundfile, у которой также имеются свои возможности анализа, и кроме того, эту библиотеку используют для записи аудио в звуковые файлы.

Для считывания и записи аудиоданных, закодированные в стандартных форматах импортируются соответствующие библиотеки в Python и вызываются соответствующие методы в Python. В листинге 1 представлено считывание аудиоданных из файла, получение его атрибутов и запись в выходной файл без изменений.

Листинг 1 – Программа, осуществляющая считывание аудиоданных из файла, получение его атрибутов и запись в выходной файл без изменений

import numpy as np

import librosa

import soundfile as sf

# считываем звуковые данные и частоту дискретизации в Гц

input_signal, Fd = librosa.load('D:/input.mp3',

sr=None, mono=False)

N = input_signal.size # количество дискретных отсчетов звука

T = N/Fd # время звучания в секундах

K = len(input_signal) # если стерео, то 2, если моно - 1

print(type(input_signal), K, N, Fd, T)

# сделаем копию, если потом захотим ее изменить:

output_signal = input_signal.copy()

# Записываем в файл. Обратите внимание на транспонирование!:

sf.write('D:/output.mp3', np.transpose(output_signal), Fd)

Индивидуальный вариант

Рисунок 1- Варинат задания

Ход работы

Меандр- сигнал, имеющий симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Форма меандра симметрична, и каждая половина цикла одинакова, длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой).

Рисунок 2- Сигнал типа меандр

Ряд Фурье для меандра в развёрнутом виде задается соотношением

,

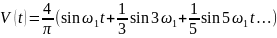где

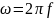
Получается, что функция для описания амплитуды сигнала в зависимости от времени, выглядит следующим образом

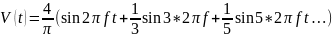
Для генерации меандрового сигнала написана функция generate_meander, которая создает сигнал путем суммирования нечетных гармоник. Сигнал дублируется для левого и правого каналов с помощью np.vstack, чтобы создать стерео сигнал. Сигнал нормализуется, чтобы его амплитуда была от -1 до 1. Для записи сигнала в WAV-файл используется библиотека soundfile (Листинг 2).

Листинг 2 –Программа создания меандрового сигнала

import numpy as np

from scipy import signal

import soundfile as sf

import matplotlib.pyplot as plt

# Параметры сигнала

Fd = 44100 # частота дискретизации)

T = 3 # длительность сигнала в секундах

N = round(T * Fd)

f = 432 # частота меандра в Гц

t = np.arange(N) / Fd

# Функция для генерации меандра через сумму гармоник

def generate_meander(t, f, num_harmonics):

signal_sum = np.zeros_like(t)

for n in range(1, num_harmonics + 1, 2): # только нечетные гармоники

harmonic = (4 / (np.pi * n)) * np.sin(2 * np.pi * n * f * t)

signal_sum += harmonic

return signal_sum

num_harmonics = 1500 # количество гармоник

meander = generate_meander(t, f, num_harmonics)

# стерео сигнал

stereo_signal = np.vstack((meander, meander))

# Нормализация сигнала

Norm = np.max(np.abs(stereo_signal))

if Norm != 0:

stereo_signal = stereo_signal / Norm

# Сохраняем в WAV файл

sf.write('meander_432hz.wav', np.transpose(stereo_signal), Fd)

Для визуализации, как количество гармоник влияет на отображение сигнала, реализованы сигналы с разным количеством гармоник. И построены графики для визуализации короткого фрагмента сигналов (Рисунок 3).

Листинг 3 – Программа визуализации сигналов с разным количеством гармоник

# Генерируем два меандровых сигнала с разным количеством гармоник

num_harmonics_25 = 25 # Количество гармоник для первого сигнала

num_harmonics_1000 = 1000 # Количество гармоник для второго сигнала

meander_25 = generate_meander(t, f, num_harmonics_25)

meander_1000 = generate_meander(t, f, num_harmonics_1000)

# Нормализация сигналов

Norm_25 = np.max(np.abs(meander_25))

if Norm_25 != 0:

meander_25 = meander_25 / Norm_25

Norm_1000 = np.max(np.abs(meander_1000))

if Norm_1000 != 0:

meander_1000 = meander_1000 / Norm_1000

# Временную ось для короткого фрагмента

short_fragment_samples = int(0.01 * Fd) # 10 мс

time_short = t[:short_fragment_samples] * 1000 # Время в миллисекундах

# График для коротких фрагментов

plt.figure(figsize=(10, 6))

plt.plot(time_short, meander_25[:short_fragment_samples], ‘r-‘, label=’25 гармоник’)

plt.plot(time_short, meander_1000[:short_fragment_samples], ‘b-‘, label=’1000 гармоник’)

plt.title(‘Короткий фрагмент сигнала (10 мс)’, pad=20, fontsize=14)

plt.xlabel(‘Время (мс)’, labelpad=10, fontsize=12)

plt.ylabel(‘Амплитуда’, labelpad=10, fontsize=12)

plt.grid(True)

plt.legend(fontsize=12)

plt.tick_params(labelsize=10)

plt.tight_layout()

plt.show()

Рисунок 3- Фрагменты меандрового сигнала для 25 и 1000 гармоник

Из рисунка можно сделать вывод, чем больше количество гармоник, тем ближе сигнал к идеальному.

Далее для анализа сформированного модельного аудиосигнала, построены графики, визуализирующие общий вид записи сигнала, его короткого фрагмента, амплитудный спектр и спектрограмма. Количество гармоник взято 1000 (Рисунок 4-7).

Используется функция sf.read для чтения WAV-файла. Также используется метод коротковременного преобразования Фурье ShortTimeFFT для анализа изменения спектра во времени. Для амплитудного спектра и спектограммы использовалась функция semilogx(), чтобы предчтавить графики в логарифмическом масштабе частоты.

Листинг 4 – Программа потсроения графиков, визуализирующих свойства сформированного модельного аудиосигнала

# Чтение аудиофайла

data, Fd = sf.read('meanderr_432hz.wav')

plt.close('all') # Очистка памяти

# Вычисляем амплитудный спектр сигнала

Spectr_input = np.fft.fft(data[:, 0]) # БПФ

AS_input = np.abs(Spectr_input) # взяли модуль

eps = np.max(AS_input) * 1.0e-9 # чтобы избежать lg(0)

S_dB_input = 20 * np.log10(AS_input + eps) # спектр в дБ

fig = plt.figure(figsize=(20, 20))

gs = plt.GridSpec(2, 2,

height_ratios=[1.2, 1.8],

width_ratios=[1.2, 1.2],

hspace=0.5,

wspace=0.3)

# Общий вид сигнала (100 мс)

ax1 = plt.subplot(gs[0, 0])

time = np.arange(len(data)) / Fd

plot_samples = int(0.1 * Fd)

ax1.plot(time[:plot_samples] * 1000, data[:plot_samples, 0], 'b-',

label='Левый канал')

ax1.plot(time[:plot_samples] * 1000, data[:plot_samples, 1], 'r--',

label='Правый канал')

ax1.set_title('Общий вид сигнала (100 мс)', pad=20, fontsize=14)

ax1.set_xlabel('Время (мс)', labelpad=10, fontsize=12)

ax1.set_ylabel('Амплитуда', labelpad=10, fontsize=12)

ax1.grid(True)

ax1.legend(fontsize=10)

ax1.tick_params(labelsize=10)

# Короткий фрагмент (10 мс)

ax2 = plt.subplot(gs[0, 1])

plot_samples = int(0.01 * Fd)

ax2.plot(time[:plot_samples] * 1000, data[:plot_samples, 0], 'b-')

ax2.set_title('Короткий фрагмент (10 мс)', pad=20, fontsize=14)

ax2.set_xlabel('Время (мс)', labelpad=10, fontsize=12)

ax2.set_ylabel('Амплитуда', labelpad=10, fontsize=12)

ax2.grid(True)

ax2.tick_params(labelsize=10)

# 3Амплитудный спектр

ax3 = plt.subplot(gs[1, 0])

f = np.arange(0, Fd/2, Fd/N) # набор частот

S_dB_input = S_dB_input[:len(f)]

ax3.semilogx(f, S_dB_input) # график в полулог. масштабе

ax3.grid(True)

ax3.minorticks_on()

ax3.grid(True, which='major', color='#444', linewidth=1)

ax3.grid(True, which='minor', color='#aaa', ls=':')

Max_dB = np.ceil(np.max(S_dB_input)/20)*20

ax3.axis([10, Fd/2, Max_dB-80, Max_dB])

ax3.set_xlabel('Частота (Гц)', labelpad=10, fontsize=12)

ax3.set_ylabel('Уровень (дБ)', labelpad=10, fontsize=12)

ax3.set_title('Амплитудный спектр', pad=20, fontsize=14)

# Добавляем вертикальные линии для основной частоты и нечетных гармоник

harmonics = [1, 3, 5, 7, 9] # номера гармоник

colors = ['r', 'g', 'b', 'm', 'c'] # цвета для разных гармоник

for i, (h, c) in enumerate(zip(harmonics, colors)):

freq = 432 * h

ax3.axvline(x=freq, color=c, linestyle='--', alpha=0.5,

label=f'{h}-я гармоника' if h > 1 else 'Основная частота')

# Легенда

ax3.legend(loc='upper left', fontsize=10, framealpha=0.9,

bbox_to_anchor=(0.02, 0.98))

# Спектрограмма

ax4 = plt.subplot(gs[1, 1])

g_std = 0.2 * Fd

wind = gaussian(round(2 * g_std), std=g_std, sym=True)

SFT = ShortTimeFFT(wind,

hop=round(0.1 * Fd), # прыгаем по 0.1 сек

fs=Fd,

scale_to='magnitude')

Sx = SFT.stft(data[:, 0])

# Преобразуем в децибелы

epss = np.max(abs(Sx)) * 1e-6

Sx_db = 20 * np.log10(abs(Sx) + epss)

colors = ['darkviolet', 'mediumorchid', 'plum', 'khaki', 'gold']

custom_cmap = LinearSegmentedColormap.from_list('custom', colors, N=100)

t_lo, t_hi = SFT.extent(N)[:2]

im = ax4.imshow(Sx_db, origin='lower', aspect='auto',

extent=SFT.extent(N), cmap='viridis')

ax4.set_title('Спектрограмма (в дБ)', pad=20, fontsize=14)

ax4.set_ylabel('Частота (Гц)', labelpad=10, fontsize=12)

ax4.set_xlabel('Время (с)', labelpad=10, fontsize=12)

ax4.semilogy()

ax4.set_ylim([10, Fd / 2])

ax4.grid(True, which='major', color='#bbbbbb', linewidth=0.5)

ax4.grid(True, which='minor', color='#999999', linestyle=':', linewidth=0.5)

ax4.minorticks_on()

ax4.tick_params(labelsize=10)

cbar = plt.colorbar(im, ax=ax4, label='Magnitude (dB)')

cbar.ax.set_ylabel('Magnitude (dB)', fontsize=12, labelpad=10)

cbar.ax.tick_params(labelsize=10)

plt.tight_layout()

plt.show()

Рисунок 4- Общий вид записи сигнала

Рисунок 5- Короткий фрагмент сигнала

По рисункам 4-5 видно, что сигнал имеет периодическую структуру, что характерно для меандра.

Рисунок 6- Амплитудный спектр

Из графика амплитудного спектра видно, что основная частота 432 Гц является самой мощной компонентой. Присутствуют только нечетные гармоники, которые убывают пропорционально.

Рисунок 7- Спектограмма сигнала

Из спектограммы видно, что основная частоты 432 Гц является самой яркой линией. Также видны горизонтальные линии на нечетных гармониках и с увеличением частоты яркость линий уменьшается.

Вывод

Успешно реализован меандровый сигнал через разложение в ряд Фурье, использовано 1000 гармоник для точного воспроизведения формы сигнала. Реализовано представление сигнала через 4 разных графика: общий вид сигнала (100 мс), детальный вид (10 мс), амплитудный спектр, спектрограмма. Амплитудный спектр наглядно показывает присутствие только нечетных гармони, видно убывание амплитуд гармоник пропорционально.

Список использованных источников

1. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №1 по дисциплине “Мультимедиа-технологии “. гр.4116,4117, 4118, Z0411. ГУАП, 2025. – 19 с. (Интернет-ресурс) URL: https://pro.guap.ru/inside/professor/tasks/2e182d6a735ab0cc0a301a18a4c84f2e/download

2. Блог о робототехнике, электронике и алгоритмах. Формы и характеристики электрических сигналов (Интернет-ресурс) URL: http://robotosha.ru/electronics/electrical-waveforms.html

3. Односевцев В.А., Орлов И.Я., Пархачёв В.В., методическое пособие по решению задач теории линейных электрических цепей- Нижний Новгород: Нижегородский госуниверситет, 2021. – 78 с., (Интернет-ресурс) URL: http://old.lib.unn.ru/students/src/2833.pdf