1. Фундаментальные свойства электрического заряда. Закон сохранения заряда. Закон Кулона.

Электрический заряд — это физическая величина, которая показывает способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.

Единица измерения заряда – кулон.

Свойства:

1. Квантование заряда

Заряд не может быть любым. Он существует только в виде целых кратных элементарному заряду — заряду электрона (или протона, по модулю).

То есть:

q=±ne, где e≈1.6⋅10−19 Клe≈1.6⋅10^-19 Кл,

2. Сохранение заряда

Электрический заряд не создаётся и не исчезает из ниоткуда, он может только перераспределяться.

∑q_до =∑q_после

3. Двухполярность (существование двух типов зарядов)

Заряды бывают двух видов:

положительные (например, у протона)

отрицательные (например, у электрона)

Закон сохранение электрического заряда

Алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.

Закона Кулона: Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды отталкиваются, а разноименные притягиваются. F = (kq₁q_{2)/(эпссилон} * r²⁾)

2. Электрическое поле. Его напряженность и силовые линии. Принцип суперпозиции. Напряженность поля точечного заряда.

Электрическое поле. Для объяснения природы электрических взаимодействий заряженных тел необходимо допустить наличие в окружающем заряды пространстве физического агента, осуществляющего это взаимодействие. В соответствии с теорией близкодействия, утверждающей, что силовые взаимодействия между телами осуществляются через посредство особой материальной среды, окружающей взаимодействующие тела и передающей любые изменения таких взаимодействий в пространстве с конечной скоростью, таким агентом является электрическое поле.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.

Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q_пр. Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд q_пр, помещенный в рассматриваемую точку поля, к величине этого заряда.

Принцип суперпозиции. Напряжённость поля, создаваемого системой неподвижных точечных зарядов q₁, q₂, q₃, …, q_n, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:                                           

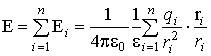
где r_i – расстояние между зарядом q_i и рассматриваемой точкой поля.

Принцип суперпозиции, позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в системах, где имеет место непрерывное распределение заряда. Заряд тела можно представить, как сумму элементарных точечных зарядов dq.

При этом, если заряд распределен с линейной плотностью τ, то dq = τ dl; если заряд распределен с поверхностной плотностью σ, то dq =  dl и dq = ρ dl, если заряд распределен с объёмной плотностью ρ.

Напряженность поля точечного заряда. Используя закон Кулона найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:

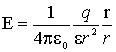   (1.2)

В этой формуле r – радиус-вектор, соединяющий заряды q и q_пр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.