Лабораторные работы / Электротехника Лабораторная работа 2

Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)

ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ ПОСТОЯННОГО ТОКА Отчет по лабораторной работе №2 по дисциплине «Электротехника»

Студент гр. 7х3-х

_______ хххххххх

_______ уууууууу

Принял: Преподаватель КИБЭВС

_______ Семенов А.С.

_______

Томск 2024

1 Введение

Цепью лабораторной работы является экспериментальная проверка расчетов, проводимых классическими методами (контурных токов, узловых потенциалов, наложения, двух узлов), на примере разветвленной цепи с тремя источниками питания.

2

2 Основные теоретические положения

В сложных, разветвленных цепях определение величины тока производится при помощи законов Кирхгофа. По первому из этих законов количество электричества, притекающее к любой точке цепи (в том числе к точке разветвления — узлу), равно количеству электричества, утекающему от этой точки; иными словами, сумма токов, притекающих к любой точке цепи, равна сумме токов, утекающих от этой точки, т.е. алгебраическая сумма токов в любой точке цепи равна нулю.

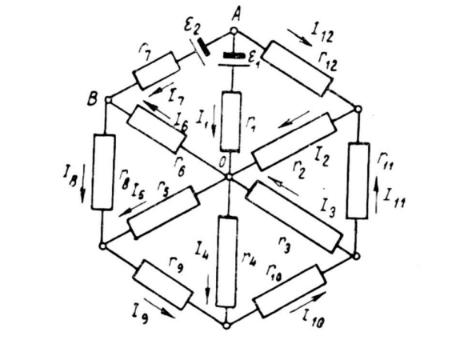
Рассмотрим узел О цепи, представленной на рисунке 2.1.

Рисунок 2.1 – Разветвленная цепь постоянного тока Если токи направлены так, как показывают стрелки, то в соответствии с

первым законом Кирхгофа:

I 1+I 2+I3=I 4+I5 +I 6

I 1+I 2+I3 – (I4 +I5+I6)=0

Со вторым законом Кирхгофа мы познакомились ранее, при рассмотрении неразветвленной цепи постоянного тока. По второму закону Кирхгофа для контура АОВ цепи:

I1 r1+I6 r6 – I7 r7=E1 – E2

3

Величины и направления токов в разветвленной цепи определяют следующим образом:

1.Обозначают стрелками предполагаемое направление тока в каждой ветви — участке цепи между двумя узлами; при этом положительным можно считать направление токов и ЭДС как по часовой стрелке, так и против часовой стрелки;

2.В соответствии с числом неизвестных составляют для каждого контура Равное число уравнений (по законам Кирхгофа);

3.Решая уравнения, определяют токи в каждой ветви.

Если в результате вычислений величина того или иного тока оказывается отрицательной, это значит, что в рассматриваемой ветви ток течет в направлении, противоположном указанному стрелкой.

Внешний вид лицевой панели макета со схемой электрической принципиальной приведен на рисунке 2.2. Питание макета осуществляется от сети переменного то ка 220 В, 50 Гц. Макет содержит три регулируемых источника питания и пять нагрузок в виде резисторов. Напряжения источников питания регулируются с помощью потенциометров в диапазоне от 1,5 В до 9 В. Для управления режимами работы источников питания используются три переключателя SA1 ...SA3. В положении переключателя “Е” соответствующий источник включен в цепь; в положении “XX”(холостой ход) источник отключен, т.е. на его месте образуется разрыв цепи; в положении “КЗ” (короткое замыкание) источник отключен, а на его месте в цепи организуется закоротка.

4

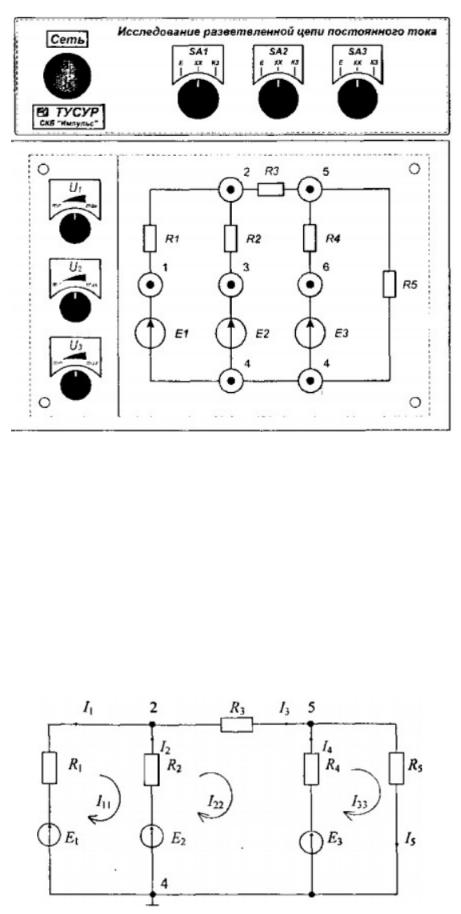
Рисунок 2.2 – Внешний вид лицевой панели макета Значения сопротивления резисторов приведены в таблице 2.1.

Таблица 2.1 – Значения сопротивлений резисторов

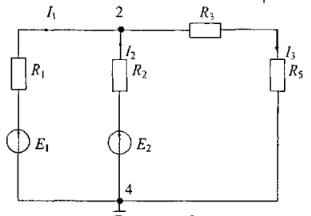
Электрическая схема изображена на рисунке 2.3.

Рисунок 2.3 – Электрическая схема

5

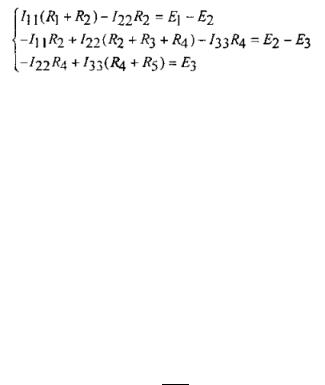
3 ХОД РАБОТЫ

3.1 Расчет токов всех ветвей методом контурных токов

Значения ЭДС, в соответствии с вариантом равны: Е1 = 2 В; Е2 = 4 В; Е3 =

6 В.

Для упрощения работы по расчету цепи ниже приведена система уравнений с учетом обозначений (рисунок 3.1).

Рисунок 3.1 – Система уравнений

Значения контурных токов составляют: I11 = –3,6 мА; I22 = 2,52 мА; I33 = 13,5 мА.

3.2 Экспериментальное определение токов всех ветвей

Для определения тока какой-либо ветви необходимо замерить с помощью вольтметра напряжение на соответствующем резисторе и, зная сопротивление резистора, пересчитать напряжение в ток по закону Ома:

In=U Rn

Rn

Результаты измерений представлены в таблице 3.1.

Таблица 3.1 – Результаты измерений

6

Продолжение таблицы 3.1

3.3 Расчет потенциалов всех узлов

Если узел 4 (см. рисунок 2.3) заземлить, то неизвестными будут потенциалы двух узлов: второго и пятого. Составленная по методу узловых потенциалов система уравнений относительно указанных неизвестных приведена на рисунке 3.2.

Рисунок 3.2 – Система уравнений

Значения потенциалов узлов составляют: ϕ2 = 3,08 В; ϕ5 = 2,7 В.

3.4 Измерение потенциалов всех узлов

Для замера потенциалов узлов первого и пятого следует один шнур вольтметра подключить к гнезду “4” макета, а другой шнур поочерёдно подключать к гнёздам “2” и “5”. Результат измерений занесён в таблицу 3.2.

7

Таблица 3.2 – Результаты измерений потенциалов

3.5 Экспериментальная проверка выполнения второго правила Кирхгофа для контура 4, 2, 5, 4

Согласно второму правилу Кирхгофа в любом замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме напряжений на нагрузках. Поэтому для выполнения данного пункта следует замерить напряжения на зажимах источников Е2 и Е3 и напряжения на резисторах R2, R3, R4 при измерениях необходимо учитывать полярности напряжений, приняв за направление обхода контура при проведении измерений направление контурного тока I22 на рисунке 2.3 (переключаясь вольтметром с одного элемента на другой переносить оба шнура, не изменяя их последовательности).

Результаты измерений представлены в таблице 3.3.

Таблица 3.3 – Проверка второго правила Кирхгофа

3.6 Экспериментальная проверка метода наложения

Согласно методу наложения ток в любой ветви электрической цепи равен алгебраической сумме частичных токов этой ветви. Поэтому для выполнения пункта требуется собрать поочередно три частичные схемы (по количеству источников в исследуемой цепи), которые приведены на рисунке 3.3.

8

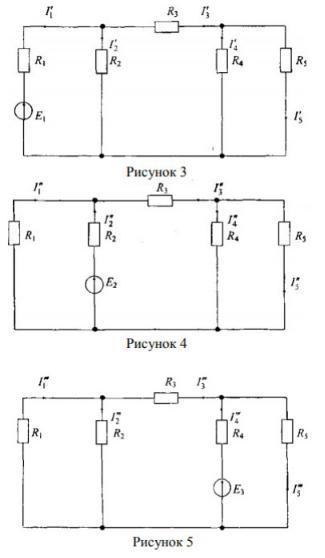
Рисунок 3.3 – Схемы

Результаты измерений и подсчетов занесены в таблицу 3.4.

Таблица 3.4 – Частичные токи ветвей

9

Продолжение таблицы 3.4

3.7 Расчет методом двух узлов схемы

На рисунке 3.4 представлена схема для расчета методом двух узлов.

Рисунок 3.4 – Схема Расчётные соотношения представлены на рисунке 3.5.

10