
ЧМ Лабораторная работа 1
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)
ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ). ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ.
Отчет по лабораторной работе №1 по дисциплине «Численные методы»
Студент гр. 7х3-х
_______ хххххххх
_______
Принял:
Старший преподаватель КИБЭВС
_______ Катаева Е.С.
_______
Томск 2024
|
Содержание |
|
1 Введение.............................................................................................................. |
3 |
|
2 ХОД РАБОТЫ.................................................................................................... |
4 |
|
2.1 |
Решение СЛАУ. Метод Зейделя.............................................................. |
4 |
2.2 |
Решение нелинейного уравнения. Метод Ньютона............................... |
6 |
2.3 |
Решение нелинейного уравнения. Метод простых итераций............... |
7 |
Заключение............................................................................................................. |
9 |
|
Приложение А...................................................................................................... |
10 |
|
Приложение Б...................................................................................................... |
12 |
|
Приложение В...................................................................................................... |
14 |
|
2
1 Введение
Целью работы является разработка программной реализации методов Зейделя, Ньютона и простых итераций для решения систем линейных алгебраических уравнений и нелинейных уравнений ( ) = 0 с одной переменной.
3
2 ХОД РАБОТЫ
2.1 Решение СЛАУ. Метод Зейделя.
Индивидуальная система уравнений (2.1) была преобразована в явный вид (2.2).
{−19 ,98 x1+9 ,99 x2+7,27 x3=8,2;
7 ,69 x1 −18 ,46 x2+4 ,72 x3=3 ,84 ; (2.1) −8 x1+0,73 x2 −14 ,65 x3=2,4
x1= |
8 |
,2−9 ,99 x2−7 ,27 x3 |
; |
|
|
|
|
−19 ,98 |
|
|
|||
|
|
|
|
|
||
x2= |
3 |
,84−7,69 x1−4 ,72 x3 |
; |
(2.2) |
||
|
−18 ,46 |
|
||||
|
|
|
|
|||
2,4+8 x1−0,7 x2 |
|
|
|
|||
{x3= |
|
|
|
|
|
|
|
−14 ,65 |
|
|
|
|
|
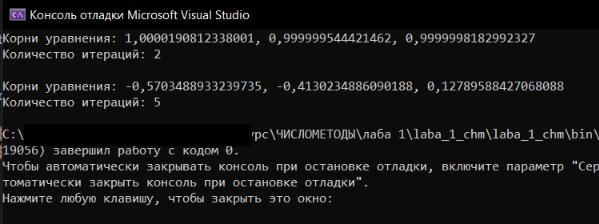
В приложении А представлен листинг программы для метода Зейделя. На рисунке 2.1 представлен результат работы программы.
Рисунок 2.1 – Результат
В таблице 2.1 представлены полученные значения для проверочной и индивидуальной систем.
4
Таблица 2.1 – Результаты решения систем
|
Начальная точка |
Число итераций |
Решение |
|
|
|
|
|
0 |
|
1 |
Проверочная система |
(0) |
2 |
(1) |
x(0)= 0 |
x(2)= 1 |
||
|
|
|
|
|
0 |
|
−0,57 |
Индивидуальная система |
x(0)=(00) |
5 |
x(5)=(−0,1280,413) |
5
2.2 Решение нелинейного уравнения. Метод Ньютона. |
|
|
Было проведено |
отделение корня с помощью графика для |
функции |
y=0 ,46 x2+0 ,81 x +0,22. В |
качестве используемых отрезков были |
выбраны |
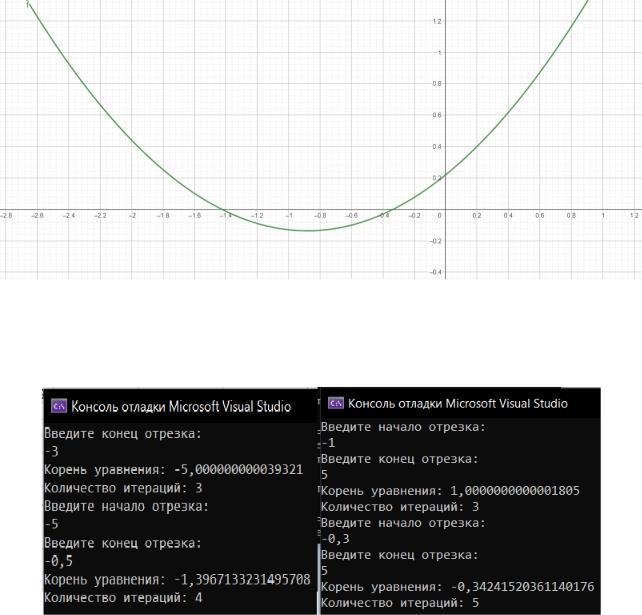
диапазоны [-5; -0,5] и [-0,3; 5]. График функции представлен на рисунке 2.2.
Рисунок 2.2 – График функции В приложении Б представлен листинг программы для метода Ньютона.
На рисунке 2.3 представлен результат работы программы.
Рисунок 2.3 – Результат
6
2.3 Решение нелинейного уравнения. Метод простых итераций.
Для метода простых итераций были взяты промежутки из пункта 2.2.
В приложении В представлен листинг программы для метода простых итераций.
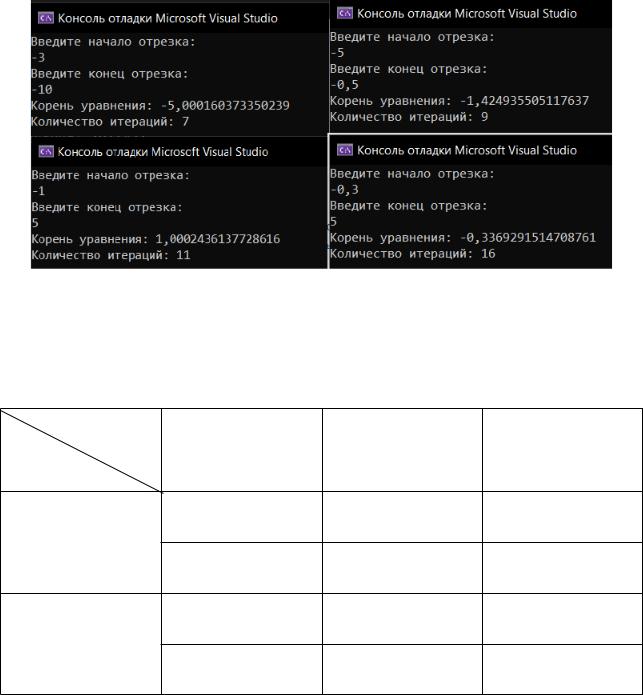
На рисунке 2.4 представлен результат работы программы.
|
Рисунок 2.4 – Результат |
|
|
В таблицах 2.2 и 2.3 представлены полученные значения для |
|||
проверочного и индивидуального уравнений. |
|
||
Таблица 2.2 – Результат решения проверочного уравнения |
|
||
Результаты |
Начальная точка |
Число итераций |
Найденные корни |
Метод |
|
для каждого корня |
|
|
|
|
|
|
x0=−6 ,5 |
3 |
-5 |
Метод Ньютона |
|
|
|
|
x0=2 |
3 |
1 |
Метод простых |
x0=−6 ,5 |
7 |
-5 |
|
|
|
|
итераций |
x0=2 |
11 |
1 |
|
|||
|
|
7 |
|
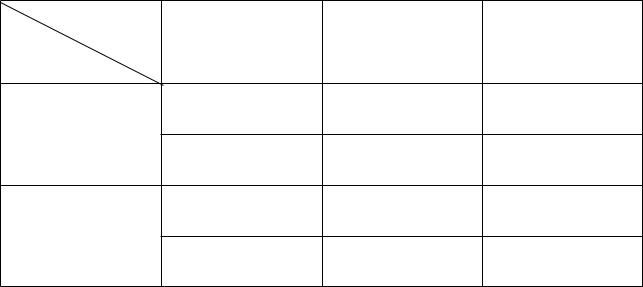
Таблица 2.3 – Результат решения индивидуального уравнения |
|||
Результаты |
Начальная точка |
Число итераций |
Найденные корни |
Метод |
для каждого корня |
||
|
|
|
|
|
x0=−2,75 |
4 |
-1,397 |
Метод Ньютона |
|
|
|
|
x0=2,35 |
5 |
-0,342 |
Метод простых |
x0=−2,75 |
9 |
-1,425 |
|
|
|
|
итераций |
x0=2,35 |
16 |
-0,337 |
|
|||
8
Заключение
В ходе данной лабораторной работы были освоены методы решения систем линейных алгебраических уравнений и решения нелинейных уравнений с одной переменной.
9
Приложение А Метод Зейделя
double start1 = 0, start2 = 0, start3 = 0; double eps = 0.001;
int iterations1 = 0; int iterations2 = 0;
void TestSeidel()
{
double x1 = (-2 * start1 - 3 * start3 + 105) / 100; double x2 = (-1 * x1 - 3 * start3 + 104) / 100; double x3 = (-1 * x1 - 2 * x2 + 103) / 100;
if ((Math.Abs(x1 - start1) < eps) && (Math.Abs(x2 - start2) < eps) && (Math.Abs(x3 - start3) < eps))
{
Console.WriteLine($"Корни уравнения: {x1}, {x2}, {x3}");
Console.WriteLine($"Количество итераций: {iterations1}");
}
else
{
iterations1 += 1;
start1 = x1; start2 = x2; start3 = x3; TestSeidel();
}
}
void TaskSeidel()
{
double x1 = (8.2 - 9.99 * start2 - 7.27 * start3) / (-19.98); double x2 = (3.84 - 7.69 * x1 - 4.72 * start3) / (-18.46);
10
