
2 курс / Анализ данных / СЛУЧАЙНЫЕ СОБЫТИЯ
.pdf
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Случайные события

ДЕПАРТАМЕНТ МАТЕМАТИКИ
При использовании классических подходов к определению основных понятий теории вероятностей необходимо, чтобы имелась возможность для многократного осуществления какого-либо испытания (опыта) при неизменных условиях.
Качественный результат испытания в таком случае называют событием.

ДЕПАРТАМЕНТ МАТЕМАТИКИ
Если событие никогда не наступит при испытании, сколько бы раз его не повторяли, то оно называется невозможным. Невозможное событие обозначают .
Если при каждом осуществлении испытания событие наступает обязательно, то оно называется достоверным.
Достоверное событие обозначают .
Если при осуществлении испытания событие может наступить, а может и не наступить, то оно называется случайным. Случайные события обозначают латинскими буквами А, В, С…
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Если событие нельзя разложить на более простые события, тогда оно называется элементарным.
Элементарные события, как правило, обозначают 1 , 2 ,… Множество всех возможных событий, связанных с данным испытанием, называют пространством событий.
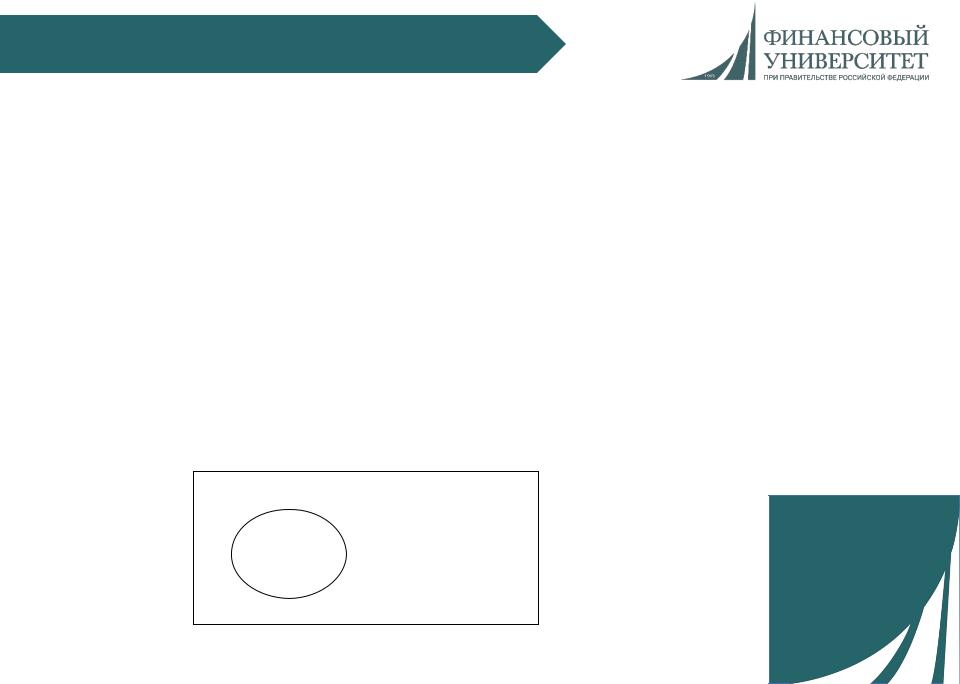
Пространство событий обозначают и изображают как универсальное множество. Тогда область наступления какого-либо события А изображают подмножеством, а элементарное событие - точкой в пространстве .
А
• 1
ДЕПАРТАМЕНТ МАТЕМАТИКИ
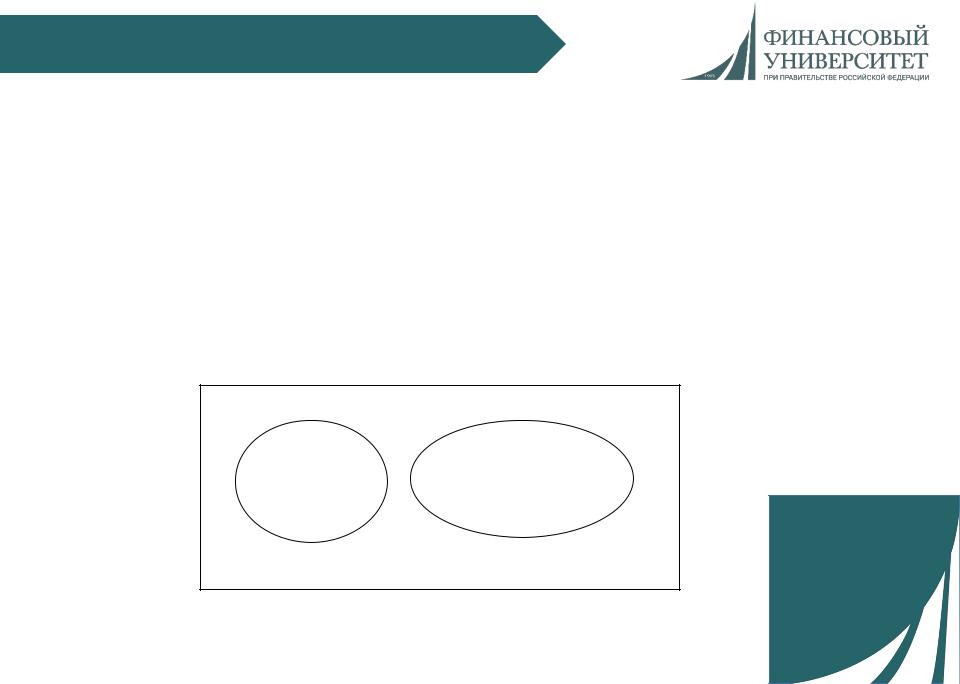
События, которые не могут наступить одновременно в одном и том же испытании, называют несовместными:
А
В

ДЕПАРТАМЕНТ МАТЕМАТИКИ
События, которые могут наступить одновременно в одном и том же испытании, называют совместными:
А |
В |

ДЕПАРТАМЕНТ МАТЕМАТИКИ
Если в одном и том же испытании при наступлении события А событие В наступает обязательно,
то говорят, что А благоприятствует В:
А
В
Если событие А благоприятствует В и, одновременно, В благоприятствует А, то события А и В определяются как равные или тождественные.

ДЕПАРТАМЕНТ МАТЕМАТИКИ
ОПЕРАЦИИ С СОБЫТИЯМИ
Для событий определены операции сложения, вычитания и умножения.
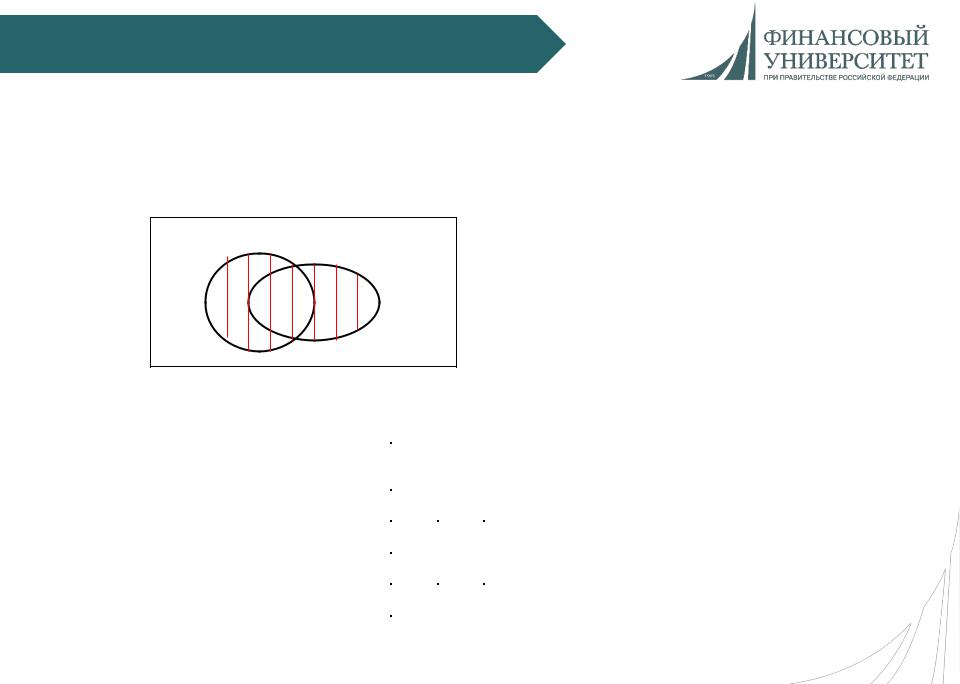
В результате выполнения операции формируется новое событие, область наступления которого можно отмечать штриховкой на диаграмме.
Для нового события можно заполнять таблицу значимости, в которой 1 обозначает факт наступления события, а 0 отмечает то, что событие не наступило.
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Суммой А + В двух событий называют новое событие, состоящее в том, что наступило хотя бы одно из событий А или В.
А |
В |
А + В
Таблица значимости для суммы событий имеет вид:
А |
В |
А+В |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
||||
1 |
0 |
1 |
|
|
0 |
1 |
1 |
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|

ДЕПАРТАМЕНТ МАТЕМАТИКИ
Произведением АВ двух событий называют новое событие, состоящее в том, что наступило каждое из событий А или В.
А В
Таблица значимости для произведения событий имеет вид:
А |
В |
АВ |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
1 |
0 |
0 |
|
|
0 |
1 |
0 |
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
