2 курс / Анализ данных / ДВУМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
.pdf
ДЕПАРТАМЕНТ МАТЕМАТИКИ
|
Z = X − Y |
|
X = 0 |
|
|
|
X =1 |
|
X = 3 |
|
X = 4 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Y = −1 |
|
0-(-1)= |
|
|
1-(-1)= |
|
|
3-(-1)= |
|
|
4-(-1)= |
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
4 |
|
|
5 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0,1 |
|
|
|
|
|
0 |
|
|
0,1 |
|
0,1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Y = 0 |
|
0-0= |
|
|
|
1-0= |
|
|
3-0= |
|
|
4-0= |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0,1 |
|
|
|
|
|
0,1 |
|
|
0,1 |
|
0,1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Y =1 |
|
0-1= |
|
|
|
1-1= |
|
|
3-1= |
|
|
4-1= |
|
|
|
|
|
|
||||||
|
|
|
|
-1 |
|
|
|
|
|
0 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0,1 |
|
|
|
|
|
0.1 |
|
|
0,1 |
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Закон распределения величины |
Z = X − Y имеет вид: |
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения Z = X − Y |
|
−1 |
|
0 |
|
|
1 |
|
|
|
2 |
|
3 |
|
|
4 |
5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятности pi |
|
0,1 |
|
0,2 |
|
0,2 |
|
0,1 |
|
0,1 |
|
|
0,2 |
0,1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Здесь
p1 = P(X − Y = −1)= P(X = 0,Y =1)= 0,1,
p2 = P(X − Y = 0)= P(X = 0,Y = 0)+ P(X =1,Y =1)= 0,1 + 0,1 = 0,2 , p3 = P(X − Y =1)= P(X = 0,Y = −1)+ P(X =1,Y = 0)= 0,1 + 0,1 = 0,2 ,
p4 |
= P(X − Y = 2)= P(X =1,Y = −1)+ P(X = 3,Y =1)= 0 + 0,1 = 0,1 |
|
p5 |
= P(X − Y = 3)= P(X = 3,Y = 0)+ P(X = 4,Y =1)= 0,1 + |
0 = 0,1, |
p6 |
= P(X − Y = 4)= P(X = 3,Y = −1)+ P(X = 4,Y = 0)= 0,1 |
+ 0,1 = 0,2 , |
p7 |
= P(X − Y = 5)= P(X = 4,Y = −1)= 0,1 |
|
n
Необходимое условие на закон распределения pi =1 выполнено.
i =1
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Теперь можем найти математическое ожидание E(Z ) ,
используя определение и полученный закон распределения:
E(Z ) =
7
zi pi = −1 0,1 + 0 0,2 +1 0,2 + 2 0,1 + 3 0,1 + 4 0,2 + 5 0,1 =
i =1
= 1,9.
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Если задан закон распределения двумерной величины (X ,Y ),
то можно ответить и на вопрос о зависимости составляющих двумерную величину компонентах X и Y .
Для этого считают ковариацию величин X и Y ,
и если ковариация не равна нулю, то величины X и Y
являются зависимыми.
Если же ковариация величин X и Y равна нулю,
то перед тем, как сделать вывод о независимости величин X и Y ,
для каждой пары значений (X = xi ,Y = y j )
проверяют выполнимость равенства:
P( X = xi ,Y = y j ) = P( X = xi ) P(Y = y j ) .
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Пример 3.
Известен закон распределения двумерной величины (X ,Y ):
|
X = 0 |
X =1 |
X = 3 |
X = 4 |
|
|
|
|
|
Y = −1 |
0,1 |
0 |
0,1 |
0,1 |
|
|
|
|
|
Y = 0 |
0,1 |
0,1 |
0,1 |
0,1 |
|
|
|
|
|
Y =1 |
0,1 |
0,1 |
0,1 |
0 |
|
|
|
|
|
Вычислить ковариацию Сov (X ,Y ).
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Решение.
Для вычисления ковариации Сov (X ,Y ) используем свойство:
.
ДЕПАРТАМЕНТ МАТЕМАТИКИ
X Y |
|
X = 0 |
|
X =1 |
|
X = 3 |
|
X = 4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 (-1)= |
|
|
1 (-1)= |
|
|
3 (-1)= |
|
|
4 (-1)= |
|
|
|
0 |
|
|
−1 |
|
|
−3 |
|
|
−4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
0 |
|
0,1 |
|
0,1 |
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
0 0= |
|
|
1 0= |
|
|
3 0= |
|
|
4 0= |
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
0,1 |
|
0,1 |
|
0,1 |
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
0 1= |
|
|
1 1= |
|
|
3 1= |
|
|
4 1= |
|
|
|
0 |
|
|
1 |
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
0.1 |
|
0,1 |
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E( X Y ) = 0 0,1 + (−1) 0 + (−3) 0,1 + (−4) 0,1 +
+ 0 0,1 + 0 0,1 + 0 0,1 + 0 0,1 + 0 0,1 +1 0,1 + 3 0,1 + 4 0 = − 0,3 .
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Чтобы найти E( X ) и E(Y ) необходимо составить распределения для X и для Y :
Значения X |
X = 0 |
X =1 |
X = 3 |
X = 4 |
|
|
|
|
|
вероятности pi |
0,3 |
0,2 |
0,3 |
0,2 |
|
|
|
|
|
E( X ) = 0 0,3 +1 0,2 + 3 0,3 + 4 0,2 = 1,9 .
Значения Y |
Y = −1 |
Y = 0 |
Y =1 |
|
|
|
|
вероятности p j |
0,3 |
0,4 |
0,3 |
|
|
|
|
E(Y ) = −1 0,3 + 0 0,4 +1 0,3 = 0 .
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Теперь ответим на вопрос задачи:
Сov (X ,Y ) = E( X Y ) − E( X ) E(Y ) = − 0,3 − 1,9 0 = − 0,3 .
ДЕПАРТАМЕНТ МАТЕМАТИКИ
Если известен закон распределения дискретной двумерной величины (X ,Y ),
то, вычислив ковариацию величин X и Y , можно найти для них и коэффициент корреляции по известной формуле
= Cov( X ,Y )
( X ,Y ) ( X ) (Y ) ,
где
( X ) = 
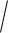D( X ) , (Y ) = 
D(Y ) .