Основные показатели деятельности банков
№ банка |
Годовая чистая прибыль, млн руб. У |
Активы-нетто млрд руб. х1 |
Собственный капитал, млн руб.X х2 |
1 |
981 |
163 |
19 |
2 |
1580 |
154 |
16 |
3 |
890 |
156 |
18 |
4 |
1 694 |
220 |
17 |
5 |
1 248 |
159 |
10 |
6 |
1 637 |
230 |
14 |
7 |
755 |
141 |
10 |
8 |
1 880 |
245 |
19 |
9 |
1 023 |
174 |
13 |
10 |
1 971 |
190 |
22 |
11 |
1 459 |
199 |
23 |
12 |
2 048 |
268 |
20 |
13 |
1 386 |
196 |
15 |
14 |
2 183 |
278 |
21 |
15 |
2 257 |
287 |
22 |
С помощью корреляционно-регрессионного анализа исследуем зависимость показателя чистой прибыли банка (у) от следующих факторов: активы-нетто (х1) и собственный капитал (х2).
Для определения парных (линейных) и частных коэффициентов корреляции составляется расчетная таблица, в которой определяются суммы значений каждого признака (у, х1, х2), их произведений (х1у, х2у, х1x2), квадратов отклонений значений каждого признака от его средней величины. На основе проведенных расчетов определяются средние значения и дисперсии. Полученные результаты представлены в приведенной ниже табл. 4.7.
Таблица 4.7
Результаты предварительных расчетов
-
Показатель
Переменные
Произведения
у
х1
х2
ух1
ух2
х1х2
Сумма
22 992
3 060
259
4 974 726
414 870
54 455
Среднее значение
1 532,8
204
17,27
331 648,4
27 658
3 630,333
Дисперсия
216 996,4
2 182,533
16,462
Среднее квадратическое отклонение
465,829
46,718
4,057
Определим парные (линейные) коэффициенты корреляции:
Таким образом, наибольшее влияние на результативный признак оказывает переменная х1 (связь тесная). Второй фактор х2 связан с у средней степенью связи.
Между факторными признаками отсутствует мультиколлениарность (т.е. тесная зависимость факторных признаков между собой), поскольку парный коэффициент корреляции между ними по модулю ниже, чем 0,8. Это означает, что оба фактора могут присутствовать в регрессионной модели одновременно.
Рассчитаем частные коэффициенты корреляции:
Как видим, связь у и х1 при условии, что х2 войдет в модель, так и продолжает оставаться тесной, хотя она незначительно снизилась с 0,871 до 0,802.
Изменилась ситуация со вторым фактором х2: введение в модель х1 сделало связь второго признака с у слабой (с 0,63 она снизилась до 0,333). Поэтому в дальнейшем регрессионном анализе стоит рассмотреть целесообразность построения парного линейного уравнения, т.е. уравнения с одной факторной переменной х1.
При выборе двухфакторной регрессионной модели следует посмотреть, насколько точно факторные переменные будут описывать вариацию зависимой переменной у. Для этого рассчитаем множественный коэффициент детерминации и множественный коэффициент корреляции:
Тогда
коэффициент детерминации равен
.
Поскольку
,
множественный коэффициент корреляции
и коэффициент детерминации требуют
корректировки.
Рассчитаем скорректированное значение
множественного коэффициента корреляции:
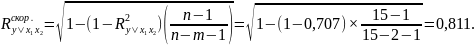
Тогда
— скорректированное значение коэффициента
детерминации. Как видим, скорректированный
коэффициент меньше нескорректированного.
Таким образом, изменение чистой прибыли
банков на 65,8% определяется изменениями
размеров их активов и собственного
капитала.
Определим
параметры двухфакторной линейной
регрессионной модели методом наименьших
квадратов. Общий вид модели:
.
Для нахождения параметров воспользуемся
следующей системой нормальных уравнений:
Подставим
в систему необходимые расчетные величины,
предварительно рассчитав дополнительные
величины
и
,
которые получились равными 656 978 и 4719
соответственно:
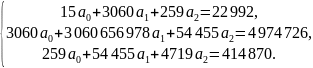
В результате решения составленной системы уравнений получаем
;
;
;
.
Непараметрические методы обнаружения взаимосвязей показателей. Корреляционный анализ относится к параметрическим методам обнаружения взаимосвязей и можно применить только по отношению к количественным показателям. Но наряду с этим существуют и другие подходы к оценке связей явлений — непараметрические методы, их реализация не требует знания законов и параметров распределения показателей.
При изучении взаимосвязей количественных признаков методами непараметрической статистики используются коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов Спирмена и др.2.
Взаимосвязь качественных признаков устанавливается с помощью коэффициентов: ассоциации, контингенции, взаимной сопряженности Пирсона, взаимной сопряженности Чупрова3.
Расчет коэффициента корреляции знаков Фехнера основывается на подсчете количества совпадений и несовпадений знаков отклонений значений показателей от их средних величин. Он определяется по следующей формуле:
,
где u — число пар, у которых знаки отклонений значений показателей от их средних совпадают;
v — число пар, у которых знаки отклонений значений показателей от их средних не совпадают.
Данный коэффициент изменяется от –1 до 1. Чем ближе его абсолютное значение к единице, тем теснее связь между признаками. Отрицательное значение коэффициента свидетельствует об обратной связи, положительное — о прямой и, соответственно, нулевое значение говорит об отсутствии связи между признаками. О тесной зависимости между признаками говорят в том случае, если коэффициент Фехнера по модулю превышает 0,7.
Пример 4. Продемонстрируем ход расчетов коэффициента Фехнера на данных о балансовой прибыли и размере основных фондов малых предприятий легкой промышленности (табл. 4.8).
Рассчитаем
средние значения х
и у.
Они получились равны:
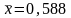и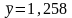
.
Определим знаки отклонений индивидуальных значений показателей от их средних. При этом знак «–» будет означать, что данное значение меньше среднего уровня показателя, «+» — больше среднего.
Таблица 4.8