Расчетная таблица для определения парного (линейного) коэффициента корреляции, параметров уравнения прямой и теоретического корреляционного отношения

Номер региона	Привлеченные средства, млрд руб. x	Размещенные средства, млрд руб. y	xy			x2
1	2	3	4	5	6	7	8	9
1	304	100	30 400	16 154,40	620,01	92 416	117	1 794,12
2	50	94	4 700	16 103,60	357,21	2 500	33	1 793,69
3	41	14	574	18 468,80	3 733,21	1 681	30	2 056,94
4	49	23	1 127	16 358,40	2 714,41	2 401	32	1 822,05
5	612	219	134 028	189 312,00	20 707,2	374 544	220	21 046,76
6	122	45	5 490	3 014,01	906,01	14 884	57	336,36
7	84	26	2 184	8 630,41	2 410,81	7 056	44	961,81
8	267	141	37 647	8 118,01	4 342,81	71 289	105	901,05
9	90	29	2 610	7 551,61	2 125,21	8 100	46	841,70
10	150	60	9 000	723,61	228,01	22 500	66	81,04
Итого	1769	751	227 760	28 4435	38 144,9	597 371	751	31 635,50

Для определения линейного коэффициента корреляции необходимо провести следующие расчеты:

1) для определения средней из произведений ху, дисперсии по х и по у проведем необходимые расчеты в графах 4, 5, 6 таблицы;

2) используя данные итоговой строки таблицы рассчитаем средние величины:

• cредняя по х: ,

• cредняя по у: ,

• средняя из произведений ху: ,

• среднее квадратическое отклонение по х: ,

• среднее квадратическое отклонение по у: ;

3) рассчитаем парный (линейный) коэффициент корреляции:

.

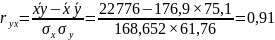Таким образом, можно сделать вывод о сильной линейной зависимости между привлеченными и размещенными средствами кредитных организаций.

Для определения параметров линейного уравнения парной зависимости проведем следующие расчеты:

• рассчитаем сумму квадратов значений признака по х в графе 7;

• для нахождения параметров и составим и решим систему уравнений:

значения параметров: и ;

• составим уравнение прямой: .

Интерпретация регрессионного коэффициента : при увеличении суммы привлеченных средств на 1 млрд руб. сумма размещенных средств увеличивается в среднем на 0,3335 млрд руб.

Для определения теоретического корреляционного отношения необходимо:

1) рассчитать теоретические (выравненные) значения результативной переменной (графа 8); для этого в полученное уравнение прямой попеременно будем подставлять значения переменной х:

• для первого наблюдения: ;

• второго наблюдения: и т.д.

Обратите внимание: сумма значений графы 8 совпадает с суммой значений графы 3; это говорит о верности проведенных расчетов по поиску параметров уравнения регрессии;

2) рассчитать сумму квадратов отклонений выравненных значений от средней величины (графа 9);

3) подставить найденные значения в формулу теоретического корреляционного отношения:

.

Как видим, по своему числовому значению оно совпало со значением парного коэффициента корреляции, что характерно для случаев сильной линейной зависимости. По данным нашего примера можно сделать вывод о том, что между показателями привлеченных и размещенных средств кредитных организаций существует тесная зависимость (обратите внимание, что интерпретация парного коэффициента корреляции была несколько иная: там мы делали вывод о силе линейной зависимости).

Дополнительно рассчитаем теоретический коэффициент детерминации:

.

Таким образом, по данным нашего примера изменение суммы размещенных средств кредитных организаций на 82,9% объясняется изменением суммы привлеченных средств.

Пример 2. По данным примера 1 проверим значимость парного (линейного) коэффициента корреляции, значимость уравнения парной регрессии и ее коэффициентов.

Проверка значимости парного (линейного) коэффициента корреляции:

1. рассчитаем наблюдаемое значение t-критерия Стьюдента:

2. выберем уровень значимости α = 0,05;

3. по таблице t-распределения Стьюдента (см. приложение) найдем критическое значение t_{крит.двуст}, соответствующее выбранному уровню значимости α = 0,05 и числу степеней свободы ν = n – 2 = 10 – 2 = 8. Получим t_крит = 2,306;

4. сравним наблюдаемое и критическое значения t .

Поскольку 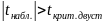, коэффициент корреляции признается значимым на уровне значимости 0,05.

Проверка значимости уравнения парной регрессии:

• рассчитаем наблюдаемое значение F-критерия:

• найдем критическое значение F_кр по таблице F-распределения Фишера (см. приложение) для числа степеней свободы: υ₁ = 1, υ₂ = n – 2 = 10 – 2 = 8, и уровня значимости α = 0,05. Для нашего примера F_кр = 5,32;

• сравним наблюдаемые и критические значения F.

Так как по данным нашего примера F_набл >F_кр, уравнение парной регрессии можно признать значимым с вероятностью 0,95 (1 – α = 0,95).

Проверка значимости регрессионных коэффициентов линейной парной регрессии:

1. определим остаточную дисперсию:

Дисперсия результативного показателя y в примере 1 ( ) была найдена при расчете среднего квадратического отклонения по у (как подкоренное выражение );

2. рассчитаем дисперсии коэффициентов:

• свободного члена а₀:

• регрессионного коэффициента а₁:

Дисперсия факторного показателя х в примере 1 ( ) была найдена при расчете среднего квадратического отклонения по x (как подкоренное выражение );

3. наблюдаемое значение t для свободного члена уравнения а₀:

4. наблюдаемое значение t для регрессионного коэффициента а₁:

5. критическое значение t находим по таблице t-распределение Стьюдента (см. приложение) при α = 0,05 и числе степеней свободы υ = n – 2 = 8. Таким образом, получаем t_{крит.двуст};

6. Сравниваем рассчитанные наблюдаемые значения t с критическим t_{крит.двуст}.

Для свободного члена неравенство не выполняется, поэтому он признается незначимым. Для регрессионного коэффициента неравенство выполняется, он значим.

Таким образом, делаем вывод, что использовать полученную модель для прогнозных целей нельзя. Незначимость коэффициента объясняется небольшим числом наблюдений (у нас их было всего лишь 10). Рекомендуемый объем выборки при парной регрессии — не меньше 15 наблюдений.

Пример 3. Проведем двухфакторный корреляционно-регрессионный анализ на основе следующих выборочных данных по 15 коммерческим банкам (табл. 4.6).

Таблица 4.6