Виды регрессионных моделей

Вид регрессионной модели	Уравнение парной регрессии (с одной факторной переменной)*	Уравнение множественной регрессии (с несколькими факторными переменными)*
Линейная
Степенная
Показательная
Параболическая
Гиперболическая

Примечание. ^* — а_j (j = 1, 2, …, m) — параметры регрессионного уравнения, называемые коэффициентами регрессии, а₀ — свободный член уравнения.

Критерием нахождения значений коэффициентов регрессии а_j является следующее требование: сумма квадратов отклонений наблюдаемых «игреков» от «игреков», рассчитанных по уравнению регрессии, должна быть минимальной. В виде формулы данное требование записывается следующем образом:

.

Метод нахождения значений коэффициентов регрессии по приведенному критерию называется методом наименьших квадратов (МНК).

Линейную функцию выбирают в качестве регрессионной модели, если результативный и факторный признаки возрастают или убывают примерно с одинаковой скоростью:

.

Коэффициент регрессии а₁ показывает, на какую величину в среднем изменится результативный признак Y, если переменную Х увеличить на единицу ее собственного измерения. Свободный член уравнения а₀ характеризует усредненное влияние неучтенных в модели факторов (определяет начальные условия развития). Параметры уравнения регрессии определяются методом наименьших квадратом путем решения системы уравнений:

где n — число пар значений x и у (число наблюдений).

Между парным коэффициентом корреляции и коэффициентом регрессии а₁ существует следующая зависимость:

и соответственно, в свою очередь, .

Рассчитанные по уравнению регрессии значения называются теоретическими (выравненными) значениями у.

При проверке значимости уравнения регрессии (если модель содержит свободный член уравнения а₀) определяют наблюдаемое значение F-критерия по следующей формуле:

,

где r_yx — парный коэффициент корреляции у с х;

n — количество наблюдений.

Критическое (правостороннее) значение F_кр находят по таблице F-распределения Фишера для числа степеней свободы: υ₁ = 1, υ₂ = n – 2, и уровня значимости α (см. приложение). Гипотеза о незначимости уравнения регрессии Н₀ отклоняется с вероятностью α, если F_набл > F_кр.

Для проверки значимость регрессионных коэффициентов используют t-критерий Стьюдента. Наблюдаемое значение t_набл вычисляется по формуле:

,

где — дисперсия соответствующего регрессионного коэффициента:

для свободного члена а₀:

регрессионного коэффициента а₁:

или _.

При регрессионный коэффициент считается значимым. Критическое значение t_кр находится по таблице t-критерия Стьюдента, при заданном уровне значимости α и числе степеней свободы υ = n – 2.

При параболической связи между признаками равномерное изменение фактора х приводит к равноускоренному изменению результативного признака у:

.

Для нахождения коэффициентов регрессии на основе метода наименьших квадратов в этом случае необходимо решить следующую систему нормальных уравнений:

Если связь между признаками обратная и при этом факторный признак по смыслу не может принимать нулевое значение, в качестве регрессионной модели выбирают гиперболическую зависимость:

.

Применение метода наименьших квадратов для нахождения параметров гиперболы приводит к следующей системе нормальных уравнений:

При анализе многофакторных связей используют уравнение множественной регрессии. Наиболее простыми для построения и анализа являются многофакторные линейные модели:

.

Параметры уравнения множественной регрессии, как и парной, рассчитываются на основе метода наименьших квадратов, при этом решается следующая система нормальных уравнений:

.

К показателям качества уравнения регрессии относят в первую очередь множественный коэффициент детерминации. Чем он выше, тем точнее выбранное уравнение регрессии описывает зависимость признаков.

В качестве критерия адекватности регрессионной модели в практике экономико-статистического анализа также используются показатели, оценивающие погрешность модели:

• средняя квадратическая ошибка уравнения регрессии:

,

m — число факторов в модели;

• средняя ошибка аппроксимации:

,

средняя ошибка аппроксимации не должны превышать 12—15%.

Средняя ошибка аппроксимации и средняя квадратическая ошибка могут использоваться при подборе наилучшей функции связи. Более адекватной считается та модель, в которой значения этих показателей меньше.

С целью расширения возможностей экономического анализа можно использовать коэффициенты эластичности:

.

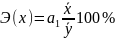Коэффициент эластичности показывает, на сколько процентов в среднем изменяется значение результативного признака при изменении факторного признака на 1%.

Пример 1. По приведенным ниже данным об объеме привлеченных и размещенных средств кредитных организаций регионов (графы 1, 2, 3 таблицы 4.5) определим парный (линейный) коэффициент корреляции, параметры линейного уравнения парной зависимости, теоретическое корреляционное отношение.

Таблица 4.5