4.2.4. Вычисление коэффициентов Фехнера и Спирмена
Вычисление коэффициентов Фехнера и Спирмена демонстрируется на рис. 4.11 по данным примеров 4, 5 и таблиц 4.9 и 4.10. На рисунке 4.11 исходные данные располагаются в столбцах С и D; диапазонам, содержащим эти данные, присвоены имена y и x. В ячейках С21 и D21 с именами Yср и Xср вычислены средние значения соответствующих показателей.
В столбцах E:F выполняются операции, необходимые для вычисления коэффициента Фехнера, а в столбцах G:H — Спирмена.
Вычисление коэффициента Фехнера. В диапазон E5:F5 введены формулы, показанные в выносках к этим ячейкам, после чего эти формулы скопированы вниз, в строку 18. Область копирования формул на рисунке окаймлена пунктирной линией. В диапазоне ОС этими формулами для каждой пары показателей (y,x) вычисляется единица, если оба значения x и y отклоняются от своих средних значений в одну сторону. В противном случае для пары (y,x) в диапазоне ОС ставится ноль. Аналогичным образом в диапазоне РС ставится единица, если в паре (y,x) оба значения y и x отклоняются от своих средних значений в разные стороны и ноль в противном случае. Сумма значений ячеек ОС и РС в ячейках E20:F20 дает величины U и V, используемые в ячейке D23, для вычисления искомого коэффициента Фехнера по формуле Excel, приведенной в Е23.
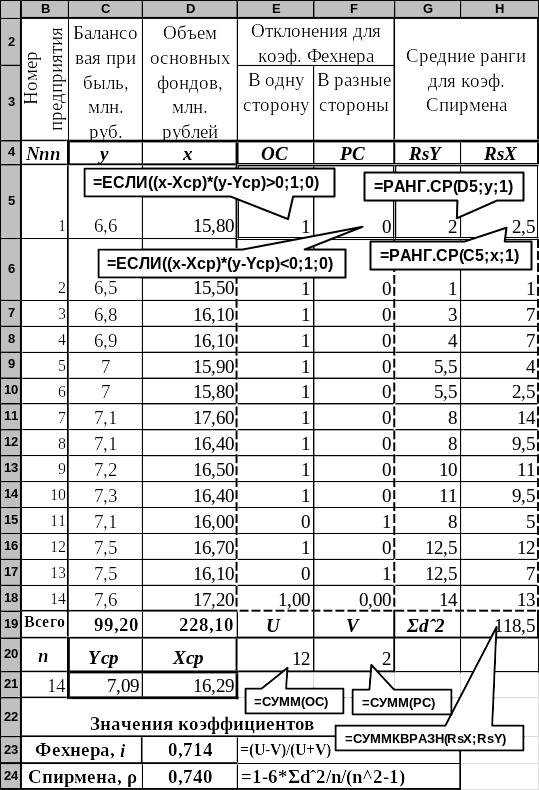
Рис. 4.11. Вычисление коэффициентов Фехнера и Спирмена
Вычисление коэффициента корреляции рангов Спирмена. Для вычисления этого коэффициента непосредственно используются не значения самих показателей, а их ранги. На рисунке 4.12 значения y (данные диапазона y на рис. 4.11) расположены для наглядности горизонтально в порядке возрастания (однако при непосредственном вычислении рангов в Excel такое упорядочивание не обязательно). В строке 2 показаны порядковые номера каждого значения y в их упорядоченном ряде (при вычислениях в Excel в такой нумерации нет нужды).
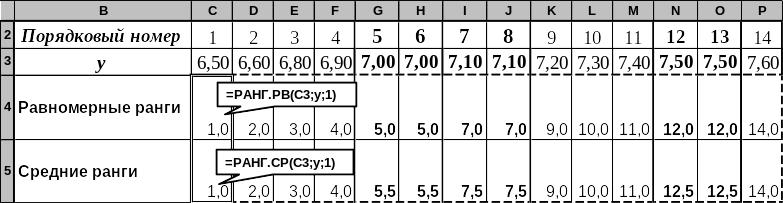
Рис. 4.12. Вычисление рангов разного типа
Если все значения y различны, то ранг каждого значения равен его порядковому номеру в упорядоченном ряде. Если среди y имеются повторяющиеся значения, то им могут быть присвоены равномерные и средние ранги, приведенные на рис. 4.12 соответственно в строках 4 и 5.
Равномерный ранг для неповторяющихся значений равен их порядковому номеру. Группа равных (повторяющихся) значений имеет один и тот же ранг, равный первому порядковому номеру в группе этих значений. Так, на рис. 4.12 совпадают пятое и шестое значения, равные 7,0. Поэтому у обеих семерок равномерный ранг равен 5. При этом отметим, что ранг 6 у значений отсутствует. Аналогичная ситуация повторяется для групп значений с порядковыми номерами 7 и 8, а также 12 и 13. Описанный способ ранжирования называется равномерными рангами по возрастанию. Если бы значения y на рисунке были упорядочены по убыванию, а ранги строились описанным способом, то они назывались бы рангами по убыванию.
В Excel равномерные ранги вычисляются с помощью функций ранг.рв(адрес, диапазон, порядок), или ранг(адрес, диапазон, порядок), аргументы которых имеют следующий смысл:
адрес — адрес ячейки со значением, для которого вычисляется ранг;
диапазон — диапазон значений, среди которых вычисляется ранг;
порядок — если аргумент опущен или равен нулю, то строятся ранги по убыванию, а при любом другом значении аргумента — по возрастанию.
Пример применения функции ранг.рв приведен на рис. 4.12 в ячейке С4, которая затем скопирована вправо.
Средний ранг равен средней величине порядковых номеров для группы одинаковых значений y. Так, для пятого и шестого одинаковых значений y5 = y6 = 7 их средние ранги равны (5 + 6) / 2 = 5,5. Как и выше, различают средние ранги по возрастанию и убыванию. В Excel средние ранги вычисляются с помощью функции ранг.ср(адрес, диапазон, порядок), в которой смысл аргументов тот же, что и у функции ранг.рв.
Вычисление коэффициента Спирмена проводится с использованием средних рангов по возрастанию значений y и x, вычисленных на рис. 5.11 в диапазонах RsY и RsX посредством рассмотренной выше функции ранг.ср.
Значение Σd2 вычисляется в ячейке H19, имеющей имя Σdˆ2 с помощью функции =СУММКВРАЗН(RsX;RsY). Значение коэффициента Спирмена вычисляется в ячейке D24 по формуле, приведенной справа от нее.