4.2.2. Анализ взаимосвязей между результативной и несколькими факторными переменными

На основе данных примера 3, представленных на фрагменте рабочего листа Excel (рис. 4.3), иллюстрируются средства анализа множественной корреляции, построения и анализа множественного линейного уравнения регрессии.

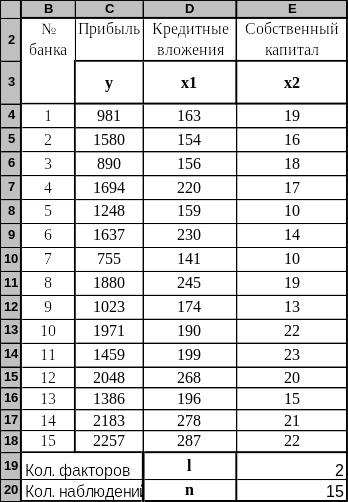
Рис. 4.3. Исходные данные примера 3

Вычисление парных (линейных) и частных коэффициентов корреляции. Для определения частных коэффициентов в Excel нет специальных инструментов. Они определяются с помощью соответствующих формул Excel, использующих значения парных (линейных) коэффициентов корреляции между изучаемыми переменными. Значения парных коэффициентов корреляции могут быть получены посредством следующих двух инструментов:

1. функции коррел, уже рассмотренной выше,

2. программы Корреляция, из Пакета анализа, вызываемой по следующей команде Excel: Данные/Анализ данных/Корреляция.

Использование функции коррел. Применение этой функции иллюстрируется на рис. 4.4.

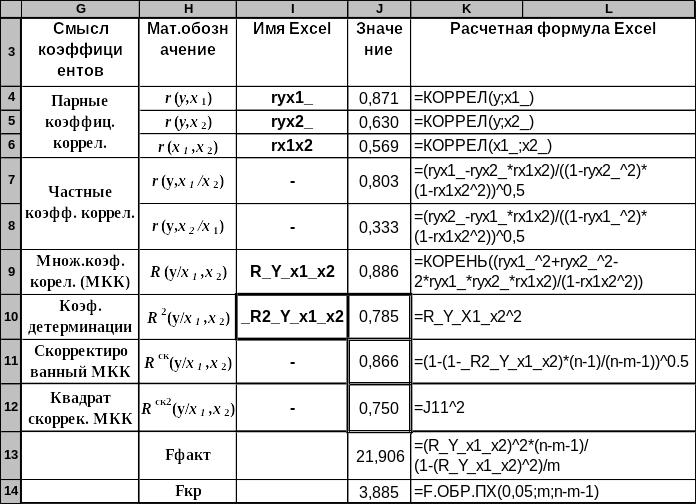
Рис. 4.4. Вычисление показателей корреляции по данным примера 3

Имена y, х1_, х2_ в формулах последнего столбца на рисунке обозначают диапазон значений соответствующих переменных y, х1, х2 на рис. 5.3. Некоторые небольшие отличия значений исчисленных показателей на рис. 5.4 от аналогичных значений, полученных в примере 3 параграфа 5.1, объясняются используемой точностью округления в промежуточных расчетах.

Отметим, что значения множественного коэффициента корреляции, коэффициента детерминации и скорректированного (нормированного) множественного коэффициента корреляции можно вычислить, используя встроенные функции, которые будут рассмотрены ниже, в подпараграфе 4.2.3.

Использование программы «Корреляция» (команды «Данные/Анализ данных/Корреляция»). С помощью программы «Корреляция» можно получить матрицу парных (линейных) коэффициентов корреляции, которые показывают связи как между факторными признаками с результативным, так и связи между самими факторными показателями (рис. 5.6). Диалоговое окно команды Данные/Анализ данных/Корреляция применительно к данным рассматриваемого примера представлено на рис. 5.5.

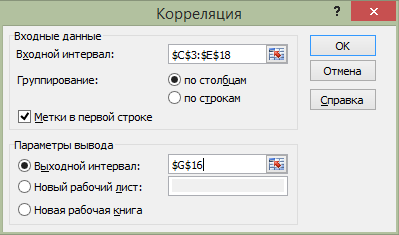
Рис. 4.5. Окно команды «Данные/Анализ данных/Корреляция» для данных примера 3

Если выделяемый интервал включает в качестве первой строки названия показателей, то следует в окошке «Метки» поставить «галочку». При расположении результатов вычислений на листе с исходной информацией в окошке рядом с опцией «Выходной интервал» следует задать ячейку, которая будет являться левым верхним углом таблицы с корреляционной матрицей. Результат вычислений по данным рассматриваемого примера представлен на рис. 5.6.

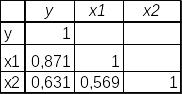
Рис. 4.6. Результат работы команды «Данные/Анализ данных/Корреляция»

В клетках этой матрицы получены те же парные линейные коэффициенты корреляции, что и при использовании функции коррел (см. рис. 4.4).

Далее можно вычислить частные линейные коэффициенты корреляции по формулам, приведенным на рис. 4.4.

4.2.3. Построение линейного множественного уравнения регрессии

Множественное линейное уравнение регрессии имеет вид:

.

Построение уравнения регрессии включает в себя нахождение коэффициентов регрессии a_i, оценка их значимости, оценка значимости и качества уравнения регрессии, а также некоторых других показателей, необходимых при использовании построенного уравнения. Для решения этой задачи существуют следующие инструменты Excel:

функция Линейн,

программа Регрессия из Пакета анализа, вызываемая командой Данные/Анализ данных/Регрессия.

Оба инструмента строят множественное линейное уравнение регрессии (МЛУР). С помощью этих инструментов также можно получить нелинейные множественные уравнения регрессии. Остановимся более подробно на расчете параметров линейного уравнения.

Существенное различие между двумя этими инструментами состоит в том, что, как и любая функция Excel, функция линейн строит динамическое решение. Это означает, что при изменении исходных данных автоматически изменяются и результаты, возвращаемые функцией. Программа Регрессия из Пакета анализа позволяет получить только статическое решение. Это означает, что при изменении исходных данных результаты вычислений не обновляются автоматически и для получения решения задачи программу Регрессия необходимо «запускать» заново.

Применение обоих инструментов продемонстрируем на данных примера 3. Лист Excel, содержащий результаты вычислений показан на рис. 5.4.

Применение программы «Пакет анализа/Регрессия» (команда Excel «Данные/Анализ данных/Регрессия»). По команде Данные/анализ данных/Регрессия открывается диалоговое окно программы, поля которого следует заполнить показанным на рис. 4.7 образом.

Рис. 4.7. Окно команды «Данные/Анализ данных/Регрессия»

Внимание! Если в поля Входной интервал Y и Входной интервал Х вводятся диапазоны данных, содержащие в том числе и названия показателей, то в окошке Метки следует поставить «галочку» (как это сделано на рис. 5.7)

После заполнения полей окна и нажатия на кнопку ОК, получим таблицы с результатами расчетов (рис. 5.8).

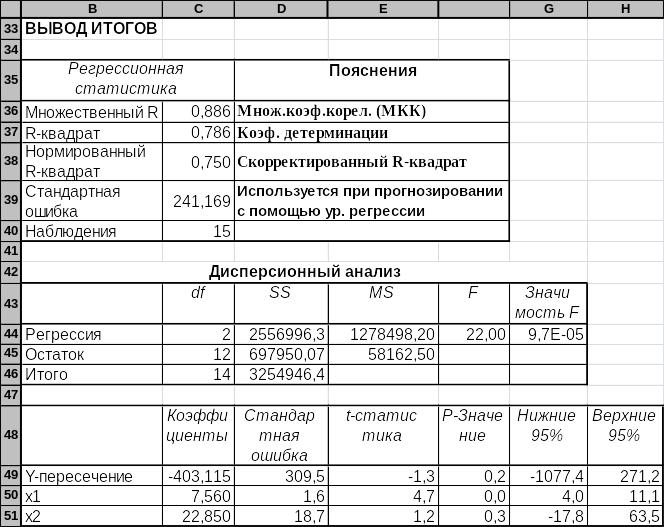
Рис. 4.8. Результаты работы программы Регрессия

Как видно из рис. 4.8, результаты сгруппированы в три блока значений. Поясним и дадим интерпретацию важнейших из них показателей⁶.

На рисунке 4.8 в блоке Регрессионная статистика в качестве справочной информации мы ввели графу Пояснения, где в ячейках уточнили названия показателей для сопоставления с полученными ранее результатами. Значения в ячейках С36, С37 этого блока совпадают с соответствующими значениями, вычисленными по формулам, на рис. 4.4. Значение же в ячейке С38 представляет собой квадрат скорректированного (нормированного) МКК из ячейки J12 на рис. 4.4.

Показатель Стандартная ошибка (ячейка Е30) используется при определении качества модели. От величины стандартной ошибки зависят пределы возможной ошибки прогнозного значения y.

Блок «Дисперсионный анализ». Выполнение условия Значимость F < α = 0,05 означает значимость построенного уравнения регрессии в целом. При этом α = 1 – Уровень надежности — это уровень значимости, где Уровень надежности = 95% задан в одноименном поле на рис. 5.7 при помеченном его обноименном флаге.

Третий (безымянный) блок расположен ниже блока дисперсионного анализа. В столбце С этого блока вычислены коэффициенты а_i уравнения регрессии, при этом Y-пересечение обозначает а₀. Отметим, что если в поле Константа-ноль в окне рис. 5.7 поставить галочку, то всегда будет а₀ = 0.

Если Р-значение для какого-либо коэффициента больше уровня значимости α = 0,05, то коэффициент признается незначимым, данную переменную следует исключить из рассмотрения и заново построить уравнение регрессии без нее.

В соответствии со сказанным оценка результатов, выдаваемых командой Регрессия, должна производиться в следующей последовательности.

1. Проверить Значимость F. Если это значение больше α, то необходимо или увеличить количество наблюдений, или увеличить α, если последнее возможно.

2. По величине Р-значения проверить значимость каждого коэффициента (переменной). Последовательно исключать переменную с наибольшим Р-значением, превышающим α, и повторять расчеты до тех пор, пока все коэффициенты (переменные) не станут значимыми.

3. По значению R² оценить, насколько хорошо уравнение регрессии описывает зависимость результативной переменой y от факторных. Если R² > 0,7, то уравнение регрессии можно использовать в дальнейших расчетах, например для прогнозирования значения y при заданных значений факторных переменных. Если количество наблюдений меньше 20, то для оценки качества уравнения регрессии следует использовать Нормированный R-квадрат (скорректированный коэффициент детерминации).

4. Дополнительные возможности команды «Регрессия». Если в диалоговом окне рис. 5.7 пометить флажок Остатки, то помимо уже рассмотренных величин для всех наблюдавшихся пар факторов (x₁x₂) будут выданы теоретические значения y_x(x₁,x₂), рассчитанные с помощью найденного уравнения регрессии, а также разности y(x₁,x₂) – y_x(x₁,x₂), между эмпирическими и теоретическими значениями y.

Применение функции Линейн. Эта функция из категории Статистические является функцией формулы массива. Это означает, что для ее применения необходимо выполнить следующие действия.

1. Выделить диапазон ячеек, в который будет помещен результат работы функции. Этот диапазон должен состоять из пяти строк и m + 1 столбцов, где m-количество факторных переменных. В соответствии с этим был выделен диапазон B23:D27.

2. Вызвать функцию ЛИНЕЙН и задать необходимые ее параметры. Так, для нашего случая были заданы параметры, показанные на рис. 4.9.

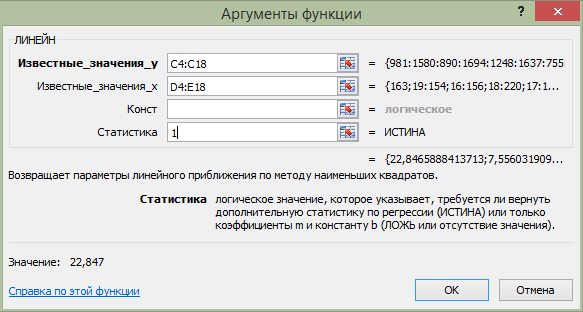
Рис. 4.9. Параметры, задаваемые для функции ЛИНЕЙН

Внимание! Диапазоны данных в первых двух полях окна не должны включать ячейки с метками переменных y, x₁, x₂ в строке 3 на рис. 5.3. Значения зависимой переменной на листе Excel могут располагаться отдельно от факторных, но факторные переменные обязательно должны располагаться в смежных столбцах.

3. Ввод параметров Линейн необходимо закончить любым из следующих способов:

одновременно нажать клавиши Ctrl + Shift + Enter;

держа нажатыми клавиши Ctrl + Shift, щелкнуть мышью по кнопке ОК в окне функции.

В результате этих действий в выделенном ранее диапазоне B23:D27 будут получены значения, приведенные в этом диапазоне на рис. 4.10. Данные строки 22 и графы Смысл значений функцией ЛИНЕЙН не выводятся автоматически и содержат только пояснения к выдаваемым функцией значениям.

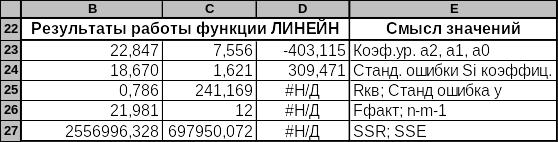
Рис. 4.10. Результат работы функции «Линейн»

Если в поле «Конст» задать ноль, то будет построено уравнение регрессии с а₀ = 0. Если поле «Статистика» оставить пустым, то будут вычислены только коэффициенты уравнения регрессии (только значения диапазона B23:D23) В этом случае для работы ЛИНЕЙН достаточно выделить диапазон из одной строки и m + 1 столбца.

Независимо от значения заданного в поле «Статистика» в первой строке выделенного диапазона в обратном порядке выдаются коэффициенты уравнения. Это значит, что коэффициент а₀ будет крайним справа, ему будет предшествовать а₁ и т.д. Так, на рис. 5.10 коэффициент а₀ выдан в ячейке D23, а₁ — в C23, а₂ — в B23. Обратите внимание, что значения ячеек B23: D23 совпадают с соответствующими коэффициентами, полученными программой Регрессия.

Отметим также, что t_i = a_i / S_i является t-значением, посредством которого проверяется значимость соответствующего коэффициента уравнения регрессии, аналогично тому, как проверяется значимость линейного коэффициента корреляции.

Смысл значений в строке 26 пояснен в графе Смысл значений. Отметим, что эти величины совпадают с соответствующими значениями выдаваемыми программой Регрессия на рис. 4.8.