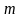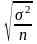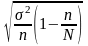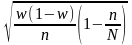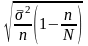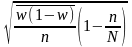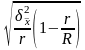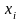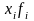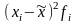Формулы расчета средней ошибки выборки

Средняя ошибка выборки
способ отбора	для средней	для доли
Собственно случайный повторный
Случайный бесповторный и механический
Типический бесповторный
Серийный бесповторный равновеликими сериями

Для малой выборки средняя (стандартная) ошибка определяется по формуле:

.

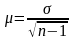Предельная ошибка выборки (Δ) равна t-кратному числу средних ошибок выборки и зависит от доверительной вероятности:

Δ = tμ.

Величина доверительной вероятности задается самим исследователем до начала сбора данных. Если из единицы вычесть значение принятой доверительной вероятности (1 – Р(t)), то получим вероятность того, что величина генеральной средней (или доли) находится за границами построенного доверительного интервала. Например, при Р(t) = 0,997 вероятность ошибочного решения будет равна 0,003 (в трех случаях из тысячи мы получим неверное заключение, т.е. и доверительный интервал не накроет оцениваемый параметр).

Коэффициент доверия зависит от величины доверительной вероятности и находится по таблице нормального распределения. Приведем ее некоторые значения (табл. 3.4).

Таблица 3.4

Выдержка из таблицы нормального распределения

Значение доверительной вероятности Р(t)	0,683	0,866	0,954	0,988	0,991	0,997	0,9999
Значение коэффициента доверия t	1,0	1,5	2,0	2,5	2,6	3,0	4,0

Если объем выборки меньше 30, то значение t уже определяется не по таблице нормального распределения, а по таблице распределения Стьюдента. Наиболее часто используемые уровни вероятности в малых выборках в зависимости от величины выборки и коэффициента доверия представлены в следующей таблице (табл. 3.5).

Таблица 3.5

Выдержка из таблицы распределения Стьюдента

T	N
	5	15	30
1,0	0,626	0,666	0,683
2,0	0,884	0,936	0,954
3,0	0,960	0,992	0,997

Доверительные границы определяются следующим образом:

• для генеральной средней — _;

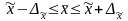• генеральной доли —

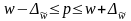
Пример 1. Для изучения уровня рентабельности продаж торговых предприятий было проведено 10%-ное выборочное обследование методом случайной бесповторной выборки, в результате которого получены следующие данные.

Рентабельность продаж,%	Число торговых предприятий	Середина интервала
до 4	9	3	27	106,50
4—6	15	5	75	31,10
6—8	12	7	84	3,76
8—10	9	9	81	58,98
10 и более	5	11	55	103,97
Итого	50		322	304,31

С доверительной вероятностью 0,954 определим, в каких границах находится средний уровень рентабельности продаж в генеральной совокупности предприятий.

1. Выборочная средняя:

%.

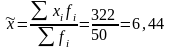2. Выборочная дисперсия:

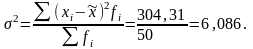
3. Средняя ошибка бесповторной случайной выборки:

.

4. При вероятности равной 0,954 предельная ошибка выборки (по таблице нормального распределения значение коэффициента доверия t = 2 при вероятности Р = 0,954):

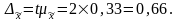
5. Доверительные границы для генеральной средней величины:

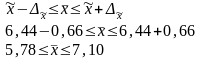
Таким образом, с доверительной вероятностью 0,954 можно сделать вывод, что в генеральной совокупности торговых предприятий средний уровень рентабельности продаж не ниже 5,78% и не выше 7,1%.

Пример 2. По данным примера 1 определим с доверительной вероятностью 0,997, в каких границах находится генеральная доля торговых предприятий, имеющих рентабельность продаж не более 8%.

1. Выборочная доля:

w = m/n = 36 / 50 = 0,72,

поскольку количество предприятий в выборке с рентабельностью продаж не выше 8% составляет 36 единиц (9 + 15 + 12 = 36), соответственно, m = 36, n = 50.

2. Выборочная дисперсия доли:

_.

3. Средняя ошибка бесповторной случайной выборки для доли:

.

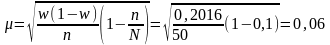4. Предельная ошибка выборки для доли (по таблице нормального распределения значение коэффициента доверия t = 3 при вероятности Р = 0,997):

5. Доверительные границы для генеральной доли:

Таким образом, с вероятностью 0,997 можно утверждать, что доля торговых предприятий с рентабельностью продаж не превышающей 8% в генеральной совокупности не менее 54% и не более 90%.

Как видим, доверительный интервал получился достаточно широкий, что снижает практическую ценность проведенного обследования. Если уменьшить величину доверительной вероятности до 0,866 (t = 1,5), то границы доверительного интервала сузятся:

Таким образом, с вероятностью 0,866 можно утверждать, что доля торговых предприятий с рентабельностью продаж не превышающей 8% в генеральной совокупности не менее 63% и не более 81%. Отсюда следует важный вывод: уменьшение величины доверительной вероятности ведет к построению более узких доверительных интервалов, но при этом увеличивает вероятность того, что построенный интервал не накроет оцениваемого параметра.

Если дисперсия доли не известна, то в расчетах берется ее максимально возможное значение — 0,25, достигаемое при w = 0,5.

Определение численности выборочной совокупности. При выборе формулы для определения численности выборки (табл. 4.6) необходимо учесть:

1. вид предполагаемой выборки;

2. способ отбора (повторный или бесповторный);

3. оцениваемый параметр (среднее значение признака или доля).

Кроме того, заранее определяют значение доверительной вероятности.

Таблица 3.6