3.2.4. Эмпирический коэффициент детерминации

В параграфе 3.1 было показано, что для оценки степени зависимости вариации значений показателя, характеризующего единицы совокупности, от признака, положенного в основу группировки, используются эмпирический коэффициент детерминации и эмпирическое корреляционное отношение. Для их расчета необходимо определить групповые дисперсии, среднюю из групповых дисперсий и межгрупповую дисперсию. Способ вычисления указанных показателей средствами Excel демонстрируется на рис. 3.17 на данных, содержащихся в диапазоне D3:K6.

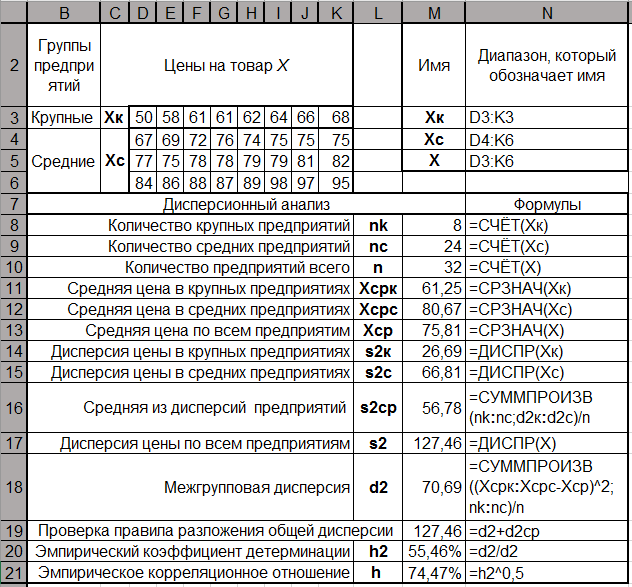
Рис. 3.17. Дисперсионный анализ

3.2.5. Показатели дифференциации и концентрации

Вид таблицы Excel с исходными данными, взятыми из таблицы примера 31 расчетными значениями, необходимыми для построения кривой Лоренца, вычисления коэффициентов Джини, Розенблата и Индекса энтропии, приведены на рис. 3.18.

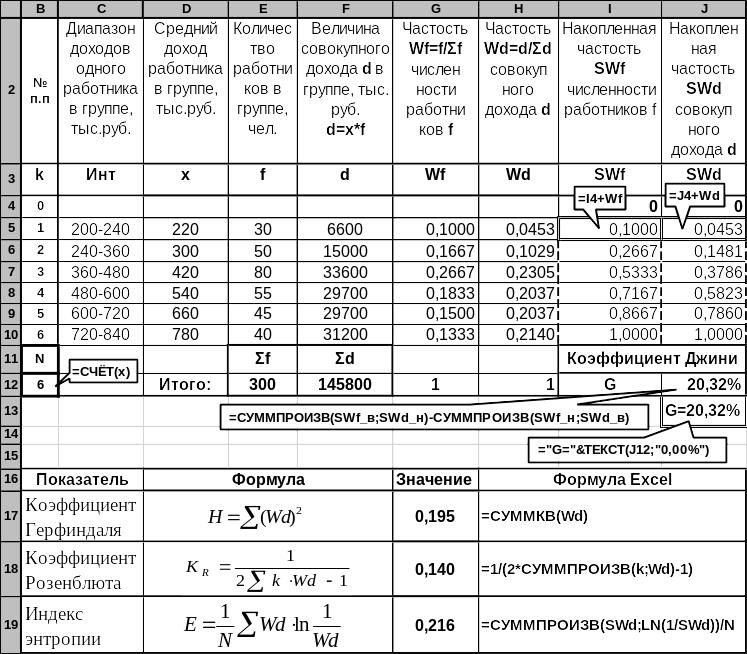
Рис. 3.18. Таблица Excel с расчетами, необходимых для построения кривой Лоренца и вычисления коэффициентов концентрации (дифференциации)

Собственно исходные данные содержатся в диапазоне С5:F10, а нули в строке 4 необходимы только при построении диаграммы на рис. 3.19 для того, чтобы график кривой Лоренца начинался в начале координат. На приведенном на рисунке листе Excel созданы имена, список которых приведен в табл. 3.16.

Таблица 3.16

Имена, созданные на листе рис. 3.17

Имя	Адрес	Имя	Адрес
k	$B$5:$B$10	SWf	$I$5:$I$10
x	$D$5:$D$10	SWf_в	$I$5:$I$9
f	$E$5:$E$10	SWf_н	$I$6:$I$10
d	$F$5:$F$10	SWd	$J$5:$J$10
Wf	$G$5:$G$10	SWd_в	$J$5:$J$9
Wd	$H$5:$H$10	SWd_н	$J$5:$J$9
Σf	$E$12	N	$B$12
Σd	$F$12	G	$J$12

Для наглядности почти все перечисленные в таблице имена приведены на рис. 3.18 в виде меток строке 3. Эти метки (имена) обозначают диапазоны данных, расположенных в столбцах под метками в строках 5:10. Обратите внимание, что ячейки строки 4 ни в одно имя не входят. Расчетные формулы, использующие эти имена, показаны в текстах строки 2 и выносках в строке 4. Эти формулы вводятся в соответствующие ячейки строки 5 и затем копируются вниз до строки 10 включительно.

Имена SWf_в и SWd_в обозначают ячейки диапазонов SWf, SWd, но без их последних ячеек в строке 10. Имена же SWf_н и SWd_н обозначают ячейки диапазонов SWf, SWd, но без их первых ячеек в строке 5. Таким образом, буквы в и н в имени обозначают соответственно верхнюю и нижнюю части диапазонов SWf и SWd. Указанные имена используются при вычислении коэффициента Джини G в ячейке J12, а в выноске к этой ячейке показана сама вычислительная формула. Математическая же формула вычисления G, использующая приведенные имена Excel, имеет вид:

.

Индексу i в этой формуле соответствуют значения i-ной строки диапазонов SWf, SWd.

Для построения диаграммы, приведенной на рис. 3.19, был выделен диапазон I3:J10 и по его значениям построена диаграмма типа Точечная со сглаженной линией ряда без маркеров, в результате чего на диаграмме была построена только кривая Лоренца.

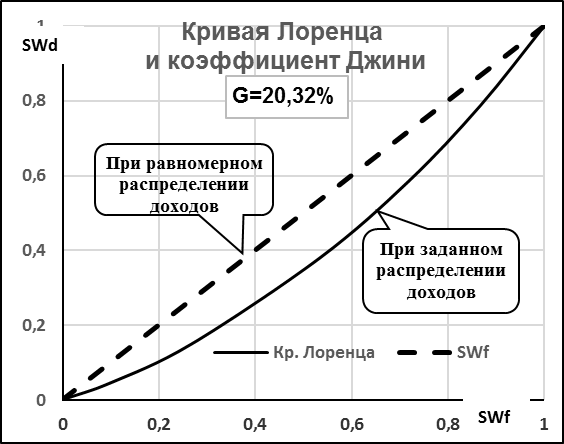
Рис. 3.19. Кривая Лоренца и коэффициент Джини

После этого пунктирная диагональ была добавлена на диаграмму с помощью следующих действий:

• скопирован в буфер обмена диапазон I4:I10;

• выделена диаграмма и в нее было вставлено содержимое буфера обмена.

Затем диаграмма была отформатирована необходимым образом (задан цвет и вид линий для рядов, указаны минимальные и максимальные значения по координатным осям, созданы название диаграммы и осей, с помощью фигуры Надпись добавлены соответствующие текстовые подписи).

Показанное на диаграмме значение коэффициента Джини динамически связано со значением ячейки J13, т.е. при изменении значения ячейки J15 будет автоматически изменяться и значение G на диаграмме. Указанный эффект получен следующим образом:

1. в ячейке J13 по формуле ="G="&ТЕКСТ(J12;"0,00%") создан текст, который должен появиться на диаграмме. Аргумент "0,00%" функции ТЕКСТ в этой формуле указывает, что значение G из ячейки J12 должно быть представлено в процентной форме с двумя знаками после запятой;

2. диаграмма была выделена и по команде ВСТАВКА/ТЕКСТ/НАДПИСЬ на ней нарисован прямоугольник — заготовка для текстового поля. Это поле должно быть выделено, т.е. на сторонах созданного прямоугольника должны быть кружки;

3. не снимая этого выделения, в строку формул введен знак равенства, выполняется щелок на ячейке J13 (т.е. создается формула =J13) и нажимается Enter. После этого в текстовом поле появляется значение ячейки J13;

4. текст форматируется необходимым образом с помощью любых инструментов форматирования шрифтов;

5. перемещением кружков на сторонах прямоугольника устанавливается необходимый его размер, после чего сам прямоугольник с текстом перемещается в требуемое место.

Следует также иметь в виду, что кривая Лоренца выглядит правильно, только если область построения диаграммы является квадратом, а прямая равномерного распределения доходов служит его диагональю. С этой целью размеры области построения диаграммы и всей диаграммы в целом следует установить соответствующим образом.

Способ вычисления коэффициент в строках 17-19 описан достаточно подробно и не нуждается в дополнительных комментариях.