Виды и задачи группировок

Аналитическая группировка

Структурная группировка

Типологическая группировка

выявление взаимосвязи между различными признаками; при аналитической группировке образование групп осуществляется по факторному признаку; затем по каждой из образованных групп исчисляются обобщающие показатели по результативному признаку

анализ состава совокупности по какому-либо варьирующему признаку; для этого однородная совокупность разделяется на группы, характеризующие ее структуру по изучаемому признаку

выделение из разнородной совокупности единиц наблюдения отдельных качественно однородных групп единиц, классов, социально-экономических типов явлений

Рис. 2.4. Виды и задачи группировок

Статистическая группировка осуществляется в несколько этапов:

1. цель группировки и выявление группировочного признака;

2. определение числа групп;

3. установление границ групп.

Определение
Группировочный признак	это признак, на основании которого происходит разбиение единиц совокупности на отдельные группы

При работе как с качественными, так и количественными признаками необходимо определить число выделяемых групп.

При группировке по количественному признаку возникает вопрос о числе групп, на которые следует разбить изучаемую совокупность.

Число групп зависит:

• от задач исследования;

• группировочного признака;

• объема совокупности;

• степени вариации группировочного признака.

Каждая группа должна характеризовать типы явлений, а число единиц в группе должно быть достаточно большим, чтобы можно было делать обоснованные выводы об исследуемой совокупности.

Оптимальное число групп можно определить с помощью различных формул. Одной из наиболее часто используемых является формула Стерджесса:

m = 1 + 3,322lgN,

где m — оптимальное число групп;

N — число единиц совокупности.

После того как определено число групп, следующим важным этапом при группировке по количественному признаку является вопрос об интервалах группировки.

Определение
Величина интервала группировки	разница между верхней и нижней границей интервала

В зависимости от исследовательских целей группировки можно использовать равные и неравные интервалы (в последнем случае равномерно возрастающие или убывающие), открытые и закрытые (рис. 2.5).

Интервалы группировки

Открытые — интервалы, у которых указана только одна граница — верхняя или нижняя; применяются только для крайних групп

Неравные — применяются при высоком размахе вариации признака в совокупности и неравномерном варьировании признака

Равные — применяются в тех случаях, когда признак колеблется в достаточно узких границах более или менее равномерно

Закрытые — интервалы, имеющие верхнюю и нижнюю границы

Рис. 2.5. Виды интервалов группировки

Если применяются равные интервалы, то их величина может быть рассчитана по следующей формуле:

_,

где x_max — максимальное значение признака в совокупности;

x_min — минимальное значение признака в совокупности.

При построении группировок с неравными интервалами для определения их величины используются формулы арифметической или геометрической прогрессии (рис. 2.6).

Определение величины интервала

Неравные интервалы

Равные интервалы

Геометрическая прогрессия

Арифметическая прогрессия

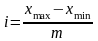
Рис. 2.6. Расчет величины интервала группировки

Статистическую группировку можно построить по одному признаку (простая группировка) или по нескольким признакам (комбинационная группировка).

В целях достижения сопоставимости данных или в иных аналитических целях проводится вторичная группировка.

Определение
Вторичная группировка	образование новых групп на основе ранее произведенной группировки без обращения к первичным данным

Для проведения вторичной группировки устанавливаются и записываются интервалы для новой группировки, определяется плотность распределения первичной группировки и число единиц, входящих в каждую группу новой группировки.

После определения группировочного признака и границ интервалов строится статистический ряд распределения.

Определение
Статистический ряд распределения	упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку

Ряды распределения могут строиться по качественному и количественному признаку и подразделяются в зависимости от этого на атрибутивные и вариационные (рис. 2.7).

Виды рядов распределения

Вариационные

(группы выделяются по количественному признаку)

Атрибутивные

(группы выделяются по качественному признаку)

Дискретные (признак принимает ограниченное число значений)

Интервальные (признак принимает множество различных значений или является непрерывным

Рис. 2.7. Виды рядов распределения

Вариационные ряды состоят из двух элементов — вариантов и частот (рис. 2.8).

Элементы статистического ряда распределения

Частота — это численность отдельных вариантов. Сумма частот — это численность всей совокупности. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями

Варианты — это значения варьирующего признака

Рис. 2.8. Виды рядов распределения

Пример 1. Имеются следующие данные об оценках 60 студентов в экзаменационную сессию:

5	3	4	5	4	2	3	4	4	5
4	5	4	3	4	3	5	3	4	5
3	4	3	4	5	3	4	5	5	2
5	3	4	5	4	3	4	5	4	4
3	4	4	5	3	4	5	2	3	4
4	5	3	4	5	4	2	4	5	4

Для того чтобы получить представление о распределении студентов по уровню успеваемости, следует построить вариационный ряд.

Признак, по которому необходимо построить ряд распределения, является дискретным (экзаменационная оценка студента). Построим дискретный вариационный ряд: для этого следует выписать все значения признака (экзаменационная оценка студента) в порядке возрастания и подсчитать число студентов по каждой группе. Экзаменационная оценка — это значения варьирующего признака (x_i), число студентов — частота вариантов (f_i), доля студентов, попавших в каждую группу, –– частость (w_i).

Экзаменационная оценка	Численность студентов	Численность студентов, в % к итогу
xi	fi	wi
2	4	7
3	14	23
4	25	42
5	17	28
Итого	60	100

Упорядоченные данные позволяют судить о распределении студентов по уровню успеваемости.

Интервальные вариационные ряды строятся при непрерывной вариации признака.

Пример 2. Имеются данные о величине вкладов в отделении банка 50 физических лиц (руб.):

5 000	65 000	92 000	75 000	59 000	88 000	13 000	55 000	105 000	76 000
78 000	35 500	11 000	30 000	65 000	25 000	22 000	58 000	85 000	81 000
40 650	27 000	15 000	12 000	71 500	22 500	13 400	49 500	40 000	47 000
45 600	61 900	55 500	62 500	80 000	9 000	30 000	55 000	91 000	45 000
34 390	59 250	26 000	28 000	37 250	53 000	50 000	59 500	73 000	56 000

Построим интервальный вариационный ряда с равными интервалами. Выделим пять групп с равными интервалами. Определим величину интервала:

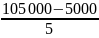= = 20 000 руб.

Определим число вкладов физических лиц в каждой группе.

Величина вклада, руб.	Число вкладов	Число вкладов, в % к итогу	Накопленная частота
xi	fi	wi	Si
до 20 000	7	14	7
20 000—40 000	12	24	19
40 000—60 000	15	30	34
60 000—80 000	10	20	44
80 000—100 000	6	12	50
Итого	50	100

В тех случаях, когда одна и та же величина встречается дважды (как верхняя граница одного интервала и нижняя граница следующего интервала), единица совокупности, обладающая этим значением, обычно относится к той интервальной группе, где эта величина выступает как верхняя граница.

Для вариационного ряда можно рассчитать накопленные частоты, которые исчисляются как нарастающий итог частот или частостей (в примере 2 — последняя графа таблицы). По накопленной частоте можно судить о том, какое число единиц в совокупности имеет значение признака не выше того значения, которое соответствует данной накопленной частоте.

При проведении анализа вариационных рядов с неравными интервалами необходимо использовать показатель плотности распределения признака. Он рассчитывается как отношение частоты или частости каждого интервала на его величину.

Результаты сводки и группировки материалов статистического наблюдения представляются в виде статистических таблиц или графиков, которые должны содержать сводную количественную характеристику изучаемой совокупности по одному или нескольким существенным признакам.

Определение
Статистическая таблица	форма наиболее краткого и рационального представления цифровых данных об изучаемой статистической совокупности

При построении статистических таблиц необходимо исходить из целей статистического исследования, содержания полученного материала, направления анализа полученных цифровых характеристик социально-экономических явлений и процессов.

На стадии сводки и группировки данных разрабатываются макеты статистических таблиц.

Определение
Макет таблицы	незаполненная цифрами статистическая таблица

Каждая таблица имеет свое подлежащее и сказуемое:

объекты или их группы, которые характеризуются приведенными в таблице статистическими данными; обычно располагается в левой части таблицы в виде наименования строк

Подлежащее

Сказуемое

признаки, цифровые данные, которыми характеризуется подлежащее таблицы

Сказуемое

В наименование таблицы раскрывается ее основное содержание.

В зависимости от характера разработки подлежащего различают основные виды статистических таблиц: простая, групповая, комбинационная.

В простой таблице в подлежащем приводится перечень каких-либо объектов, показателей, территориальных единиц. В подлежащем простой таблицы нет группировки единиц совокупности.

В качестве примера рассмотрим несколько вариантов простых таблиц. В таблице 2.2 в подлежащем приводится перечень основных показателей, характеризующих социально-экономическое развитие России, а в сказуемом представлены значения этих показателей за 2018 и 2019 г.

Таблица 2.2