Вычисление структурных средних для вариационных рядов
Напомним, что к структурным средним относится мода, медиана, квартиль 1÷квартиль 3, дециль 1÷дециль 9. Для всех перечисленных величин, кроме моды, существует обобщающее понятие «персентиль» (иногда пишется «перцентиль») P(q), где 0 ≤ q ≤ 1.
Если рассматриваемый показатель X является дискретным, то под персентилем P(q) понимается такое значение признака X, что q% всех значений X меньше или равно P(q). В рассматриваемом случае персентиль находится по упорядоченному по возрастанию набору значений X или по его дискретному вариационному ряду.
Если показатель X является непрерывной величиной, то персентиль P(q) — это такое значение, что вероятность того, что x ≤ P(q) равна q. В данном случае P(q) в статистике находится по интервальному вариационному ряду для X.
В соответствии со сказанным медиана — это персентиль для q=0,5, т.е. P(0,5), квартили — это персентили P(0,25), P(0,5), P(0,75), децили P(0,1), P(0,2), …, P(0,8), P(0,9). Ниже приводятся способы вычисления персентилей P(q) для любых значений q в случае задания X как с помощью дискретного, так и интервального вариационного ряда.
Структурные средние для дискретного вариационного ряда. Необходимо отметить, что существуют несколько различных способов вычисления структурных средних в дискретных рядах, приводящих к разным их значениям. Так, в мощной статистической программе Statistica заложены шесть таких способов. Ниже, на рис. 3.14, приводится способ вычисления структурных средних, названный в этой программе «метод Excel».
Дискретный ряд на рисунке задан значениями вариантов X и их частот F соответственно в диапазонах B5:B13 и C5 C13. Численным данным в столбцах B:D назначены имена X, F, CF. Кроме того, имя Хсм (X смещенное) присвоено диапазону B6:B14.
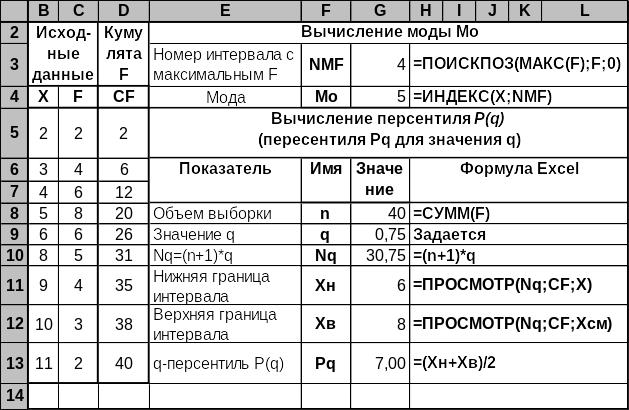
Рис. 3.14. Вычисление структурных средних для дискретного вариационного ряда
Значениям диапазона G8:G12 присвоены имена, стоящие в столбце F слева от них. На рисунке для заданного дискретного ряда вычислен третий квартиль. Изменение значения q в ячейке G9 немедленно приводит к вычислению соответствующего Pq. Однако если q таково, что Nq меньше минимального значения Х, то Pq не может быть вычислено и для него в ячейке G13 выдается значение #Н/Д.
Структурные средние для интервального вариационного ряда. Расчет моды Мо представлен на рис. 3.15 для общего случая, при котором интервальный ряд имеет различную длину интервалов. Для таких рядов моду следует вычислять не по частотам F, а по плотностям P, где P — это отношение частоты F к длине соответствующего интервала. В таком случае формула вычисления моды принимает вид:
,
где mo — индекс, обозначающий модальный интервал, т.е. интервал, имеющий наибольшую плотность. Если таких интервалов несколько, то используется первый из них;
xmo, dmo — соответственно левая граница и длина модального интервала;
Pmo, Pmo-1, Pmo+1 — плотности соответственно модального интервала, интервала, предшествующего модальному и следующему за ним.
На рисунке 3.15 вместо обозначений xmo, dmo, Pmo, Pmo-1, Pmo+1 используются имена LGm, Dm, Pm, Ppm, Psm, поскольку имена в Excel не могут иметь вид обозначений, используемых выше в математической формуле вычисления моды. Также метки из диапазона B5:E5 используются в качестве имен данных, расположенных в столбцах под ними.
При вычислении значений Ppm, Psm в ячейках H9, H10 полагается, что если модальным является первый или последний интервал, то соответствующие значения Pmo-1, Pmo+1 равны нулю.
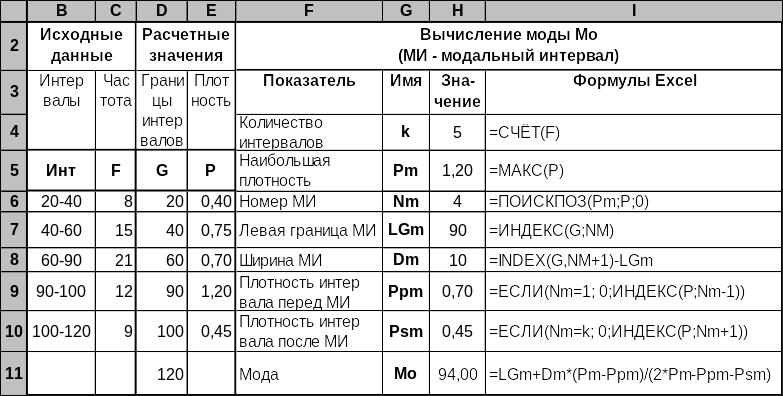
Рис. 3.15. Вычисление моды для интервально ряда
Вычисление персентиля P(q) показано на рис. 3.16 и выполняется по следующей формуле:
,
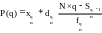где xqи, dqи — левая граница и длина персентильного интервала;
N, q — объем выборки и значение q;
Sqи-1 — накопленная частота интервала, предшествующего персентильному. Если персентильным является первым интервал, то полагается, что Sqи-1 = 0;
fqи — частота персентильного интервала.
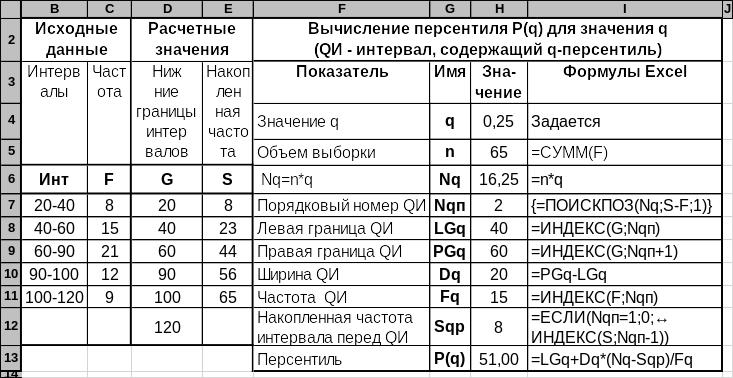
Рис. 3.16. Вычисление персентиля для интервально ряда
На рисунке 3.16 вместо обозначений xmo, dmo, Pmo, Pmo-1, Pmo+1 используются имена, приведенные на рисунке в диапазоне G4:G13, поскольку имена в Excel не могут иметь вид обозначений, используемых выше в формуле вычисления персентиля. Представляется, что смысл этих обозначений ясен из пояснений в ячейках слева от них. Кроме того, метки в диапазоне B6:E6 используются в качестве имен данных, расположенных в графах под ними.
Под порядковым номером Nqп понимается порядковый номер персентильного интервала в диапазоне B7:B11. Обратите внимание, что формула его вычисления в ячейке H7 вводится как формула массива, т.е. ввод формулы заканчивается по ENTER при одновременно нажатых клавишах CTRL + SHIFT. Об этом свидетельствуют фигурные скобки, в ячейке I7, показывающей вид формулы в H7 (о работе с формулами массива см. также подпараграф 2.2.2).