ТУСУР |
25 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
Многолучевость в радиоканале. Мультипликативные помехи
A(t)
Aс
Aп
t
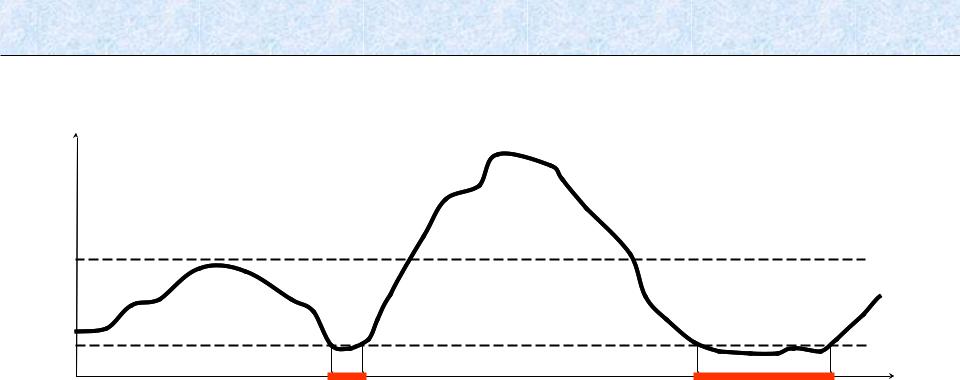
Пример флуктуаций амплитуды принимаемого сигнала в канале с многолучевостью.
Существуют такие случайно расположенные интервалы времени случайной длительности (помечены жирными линиями), когда амплитуда падает ниже уровня Aп, при
котором еще возможен нормальный прием сигнала.
ТУСУР |
26 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
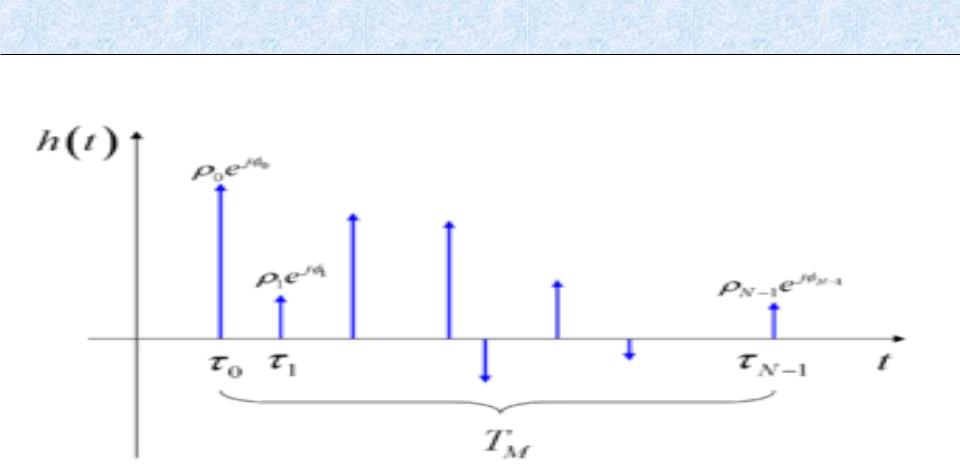
Мультипликативные помехи
Математическая модель импульсного отклика линии с многолучевостью
ТУСУР |
27 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
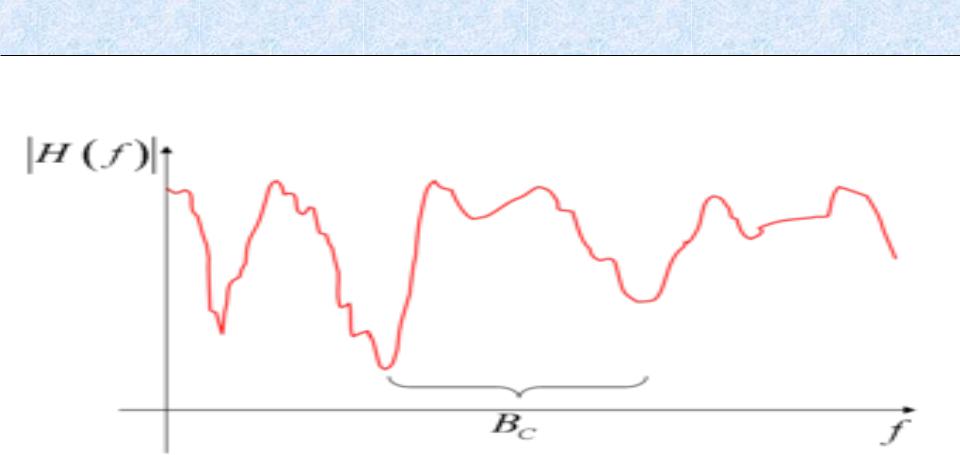
Мультипликативные помехи
Математическая модель частотной характеристики линии с многолучевостью
ТУСУР |
29 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
Методы аналитического и геометрического представления сигналов и помех
U t A t cos t A t cos 0t t ,
- реальный сигнал
U t C t cos 0t S t sin 0t,
квадратурные составляющие
C t A t cos t
S t A t sin t
ТУСУР |
30 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
Методы аналитического и геометрического представления сигналов и помех
|
|
|
|
|
|
|
|
Аналитический сигнал |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
u |
t |
A |
t |
t i |
t |
U (t) exp |
t |
, |
||||||||||||
|
|
|
|
exp i |
|
|
|
i |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U t Re u(t) .
|
|
t |
|
|
|
t |
|
|
U (t) A |
|
exp i |
|
|
||||
|
A t cos t |
iA t sin t C t iS t . |
||||||
ТУСУР |
31 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
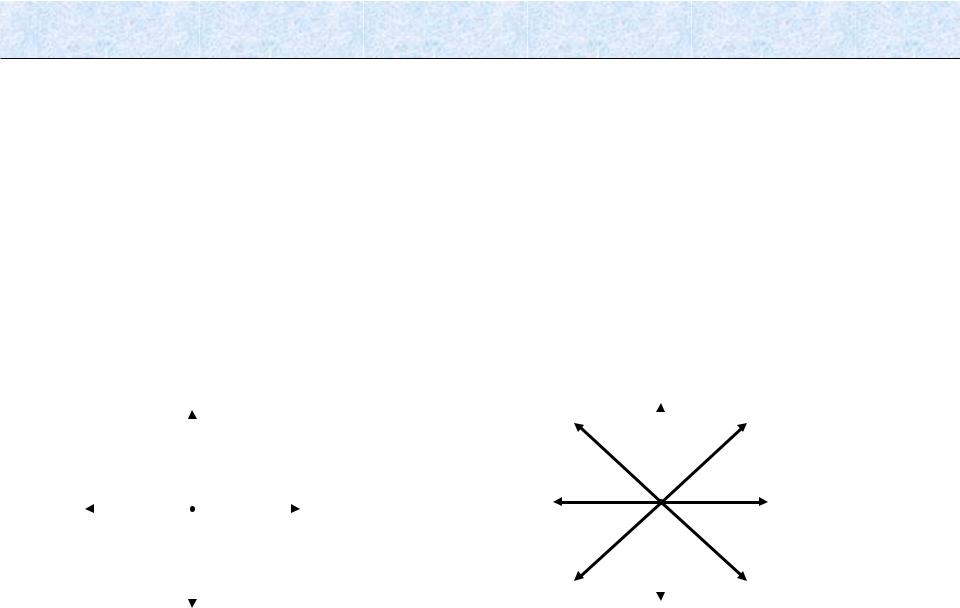
Векторное представление колебаний при многократной ФМ
а) k=1, M=2
1 
0
|
б) k=2, M=4 |
|
в) k=3, M=8 |
||||||
|
|
2 |
|
→010 |
|
||||
|
|
|
1→01 |
3→011 |
|
1→001 |
|||
|
|
|
|
||||||
|
|
|
|
|
|
||||
2→10 |
|
0→00 |
4→100 |
|
|
|
0→000 |
||
|
|
|
|
|
|
|
|
||
|
|
|
3→11 |
5→101 |
|
|
|
7→111 |
|
|
|
|
6→110 |
||||||
|
|
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
ТУСУР |
32 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
Геометрическое представление непрерывного сигнала в евклидовом пространстве
U |
|
t |
|
1 |
2 |
,...,U |
n |
1 |
2 |
n |
) |
t , |
|
|
U U |
,U |
|
(u |
,u |
,...,u |
|||||
|
|
|
|
|
|
|
|
- отсчеты с шагом |
t |
|||
Норма (длина) |
|
|
|
n |
вектора U в |
|
U |
|
2 |
|
|
|||
евклидовом |
|
|
U j . |
|
|
|
|
||
пространстве |
|
|
|
j 1 |
|
|
|
|
ТУСУР |
33 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
Геометрическое представление непрерывного сигнала в евклидовом пространстве
Расстояние между двумя непрерывными сигналами U(t) и V(t)
d U,V lim |
n |
|
2 t |
T |
|
|
2 |
|
|
u j vj |
U |
t V |
t |
dt |
|||
t 0 |
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Скалярное произведение двух векторов U и V
|
|
|
|
|
n |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
j |
j |
|
|
|
|
|
||||||||||
U,V |
t 0 |
|
t |
|
V |
t |
dt. |
|||||||||||
|
|
lim |
|
|
u |
v |
|
|
U |
|
t |
|
|
|||||
|
|
|
|
j 1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
||
ТУСУР |
34 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
Геометрическое представление цифрового (двоичного) сигнала в n-мерном пространстве Хэмминга
S S1, S2 ,..., Sn
-последовательность символов (кодовая комбинация)
Суммирование по модулю 2
0 0 0, 0 1 1 0 1, 1 1 0
Длина вектора - его вес S W S
ТУСУР |
35 |
Теория электрической связи |
|
Профессор кафедры радиотехнических систем Ю.П. Акулиничев |
Геометрическое представление цифрового (двоичного) сигнала в n-мерном пространстве Хэмминга
Скалярное произведение
S,C S1 C1 S2 C2 |
0 |
, |
... Sn Cn |
||
|
1 |
|
Расстояние Хэмминга
n
d S,C W S C S j Cj ,
j 1