2.5 Спектры сигнала при широтно-импульсной модуляции (шим)

При ШИМ длительность импульсов изменяется по закону, отображающему характер модулирующей функции .

Различают: одностороннюю модуляцию по длительности (ОШИМ) – модулируется один из фронтов импульса (передний или задний); двустороннюю (ШИМ) - модулируются оба фронта (рис. 2.15); модуляцию первого и второго рода.

При модуляции первого рода момент нарастания (спадания) фронта импульса определяется значением модулирующей функции в этот же момент. Длительность модулированного импульса равна

,

(2.29)

где – длительность немодулированного импульса, – максимальное изменение (девиация) длительности при модуляции.

При модуляции второго рода момент нарастания (спадания) напряжения каждого импульса определяется значением модулирующей функции в момент времени, соответствующей тактовой точке, то есть

(2.30)

Вычисление спектров при ШИМ (ОШИМ) достаточно сложно даже для случая синусоидальной модулирующей функции. Разработаны [1] специальные методы расчёта спектров. Здесь приводятся окончательные результаты. Наиболее широкое применение находят сигналы с ОШИМ.

2.5.1 Спектр сигнала с ошим-1

Для синусоидальных импульсов спектр ОШИМ-1 может быть получен в виде

(2.31)

где – частота модуляции;

m – номер гармоники частоты модуляции;

F – частота повторения;

n – номер гармоники частоты повторения;

– комбинационные частоты;

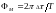– индекс модуляции;

J_m – функция Бесселя первого рода m-го порядка.

Спектр ОШИМ-1 изображён на рис. 2.16.

Как следует из (2.31), спектр ОШИМ-1 содержит теоретически бесконечное количество комбинационных частот . Амплитуды полезной и боковой частот зависят от индекса модуляции . При уменьшении

амплитуды комбинационных частот уменьшаются, но при этом снижается и амплитуда полезной составляющей.

При малых индексах модуляции уровень комбинационных составляющих мал и условия аналогичны случаю АИМ.

Так как функция Бесселя есть монотонная функция своего аргумента , то с ростом номера гармоники n увеличиваются амплитуды комбинационных частот, и при n>2 боковые полосы практически перекрываются. Это делает невозможным демодуляцию ОШИМ полосовым фильтром и, как правило, используют ФНЧ.

Рис. 2.15 – Сигналы с ШИМ и ОШИМ

Рис. 2.16 – Спектры сигналов с ОШИМ-1,2 и ШИМ-1,2

Однако в отличие от АИМ-1, даже в случае идеального ФНЧ, искажения всегда имеют место. Расчеты показывают, что для обеспечения допустимых искажений при демодуляции ОШИМ-1 ФНЧ необходимо выбирать коэффициент следования импульсов .

2.5.2 Спектр сигнала с шим-1

Выражение для спектра ШИМ-1 при синусоидальной модуляции и прямоугольной форме импульса может быть получено в виде

(2.32)

Спектр ШИМ-1 изображён на рис. 2.16.

Сравнивая выражения (2.31) и (2.32), можно сделать следующие выводы:

1. амплитуда полезной составляющей (с частотой ) при ШИМ-1 за счет модуляции обоих фронтов импульса в два раза больше, чем при ОШИМ-1 (это справедливо, если максимальный сдвиг каждого фронта при ШИМ равен максимальному сдвигу фронта при ОШИМ);

2. часть комбинационных частот при четных m, попадающих в полосу ФНЧ, при ШИМ-1 имеет значительно меньшую интенсивность, чем при ОШИМ-1. Следовательно, нелинейные искажения при прочих равных условиях будут меньше.