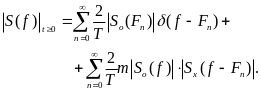2.3 Спектр сигнала при амплитудно-импульсной модуляции первого рода (аим-1)

При АИМ-1 величина напряжения внутри импульса пропорциональна значению модулирующей функции в соответствующий момент времени

(2.20)

Подставляя уже известное выражение (2.17), описывающее периодическую последовательность импульсов , для модуля спектральной плотности АИМ-1 получим

(2.21)

и для одностороннего спектра

(2.22)

где – спектр модулирующего сигнала , перенесенный на частоту

.

В правой части выражения (2.22) первое слагаемое определяет значения спектральной плотности на частотах, кратных частоте сле­дования импульсов, второе – боковые полосы, определяемые спектром модулирующего сигнала (рис. 2.10).

Для последовательности прямоугольных импульсов, модулированных по закону АИМ-1 гармоническим колебанием вида

со спектром

после преобразований (2.22) спектр будет описываться следую щим выражением

(2.23)

Рис. 2.10 – Спектр сигнала при АИМ-1

Последовательность прямоугольных импульсов с АИМ-1 приведена на рис.2.11, а ее спектр – на рис. 2.12.

Спектр содержит постоянную составляющую ( ) с амплитудой , составляющие, кратные частотам повторения импульса с амплитудами , и боко­вые частоты ( ) с одинаковыми амплитудами, определяемыми спектральной плотностью импульса на частоте повторения

Рис. 2.11 – Последовательность импульсов с АИМ-1

Рис. 2.12 – Спектр последовательности с АИМ-1

Из структуры спектра следует, что демодуляция сигнала с АИМ-1 возможна:

1) полосовым фильтром (в [3] показано, что такой способ обладает низкой эффективностью);

2) фильтром низких частот (ФНЧ), и это наиболее широкий способ применения.

В случае идеального ФНЧ с характеристикой

где - коэффициент передачи,

- частота среза фильтра,

условие неискаженной передачи спектра (отсутствие перекрытия спектра) может быть представлено в виде

(2.24)

где верхняя (граничная) частота в спектре модулирующего сигнала.

Отсюда коэффициент следования импульсов и, следовательно, период повторения удовлетворяет условию теоремы отсчетов Котельникова.

При использовании реального ФНЧ (например, при аппроксимации частотной характеристики ФНЧ гауссовской кривой), коэффициент должен быть больше двух, практически он оказывается в пределах 3,0 - 3,5.

2.4 Спектр сигнала при амплитудно-импульсной модуляция второго рода аим-2

В случае АИМ-2 амплитуда импульса при модуляции изменяется пропорционально значению модулирующей функции в тактовые моменты времени (рис. 2.13).

Модулированная последовательность импульсов имеет вид

(2.25)

где тактовые моменты времени.

Рис. 2.13 – Последовательность АИМ-2

Рис. 2.14 – Спектр последовательности АИМ-2

Так как множитель зависит от и не может быть вынесен за знак суммы, вычисление спектра усложняется. Пользуясь специальными методами расчета спектров [2], можно получить следующие результаты

	(2.26)
	(2.27)

Сравнивая выражения для спектров АИМ-1 (2.22) и АИМ-2 (2.27), нетрудно видеть, что их частотный состав одинаков; отличие заключается в том, что амплитуды боковых составляющих в спектре АИМ-1 определяются значениями спектральной плотности для частоты повторения , а в спектре АИМ-2 значениями спектральной плотности для своей частоты . То есть при АИМ-2 спектр сообщения переносится на частоту повторения с частотными искажениями (при АИМ-1 этот перенос осуществляется без искажений). Это особенно хорошо видно при модуляции гармоническим колебанием: тогда спектр АИМ-2 имеет вид

(2.28)

Спектр АИМ-2 приведен на рис. 2.12. Здесь, как и при АИМ-1, амплитуда на частоте повторения равна , а амплитуды боковых различны: составляющие с частотами имеют амплитуды , а составляющие с частотами имеют амплитуды .

Величина искажений в спектре АИМ-2 зависит от соотношения где - период модулирующего напряжения. При разница между АИМ-1 и АИМ-2 исчезает и искажения отсутствуют. При увеличения искажения увеличиваются: это сказывается при демодуляция сигнала фильтром нижних частот.