- •Исследование спектров импульсно-модулированных сигналов
- •Содержание
- •1 Введение
- •2 Некоторые сведения из теории
- •2.1 Понятие о спектре
- •2.2 Спектр периодической последовательности прямоугольных импульсов
- •2.3 Спектр сигнала при амплитудно-импульсной модуляции первого рода (аим-1)
- •2.4 Спектр сигнала при амплитудно-импульсной модуляция второго рода аим-2
- •2.5 Спектры сигнала при широтно-импульсной модуляции (шим)
- •2.5.1 Спектр сигнала с ошим-1
- •2.5.2 Спектр сигнала с шим-1
- •2.5.3 Спектр сигнала с ошим-2
- •2.5.4 Спектр сигнала с шим-2
- •2.6 Спектр сигнала с время-импульсной модуляцией (вим)
- •2.6.1 Спектр сигнала с вим-1
- •2.6.2 Спектр сигнала с вим-2
- •3 Описание лабораторной установки
- •3.1 Структурная схема
- •3.2 Конструкция лабораторной установки
- •4 Порядок выполнения лабораторной работы
- •5 Контрольные вопросы
- •6 Список литературы
Федеральное агентство по образованию РФ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
Акулиничев Ю.П., Дроздова В.И.
Исследование спектров импульсно-модулированных сигналов
Одобрено кафедрой радиотехнических систем в качестве учебно-методического пособия к лабораторным исследованиям для студентов специальностей:
071700 "Физика и техника оптической связи", 200700 “Радиотехника,” 201100 "Радиосвязь, радиовещание и телевидение", 201200 “Средства связи с подвижными объектами”, 201600 “Радиоэлектронные системы”, 201800 “Защищенные системы связи”.
Томск, 2006
Содержание
1 ВВЕДЕНИЕ ………………………………………………. 2 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ …..………. 2.1. Понятие о спектре ………………………………… 2.2. Спектр периодической последовательности прямоугольных импульсов ………………………………………. 2.3. Спектр сигнала при амплитудно-импульсной модуляции первого рода (АИМ-1) ………………………………. 2.4. Спектр сигнала при амплитудно-импульсной модуляция второго рода АИМ-2 ………………………………… 2.5. Спектры сигнала при широтно-импульсной модуляции (ШИМ) ……………………………………………….. 2.5.1. Спектр сигнала с ОШИМ-1 ………………….. 2.5.2. Спектр сигнала с ШИМ-1 …………………….. 2.5.3. Спектр сигнала с ОШИМ-2 …………………… 2.5.4. Спектр сигнала с ШИМ-2 ……………………. 2.6. Спектр сигнала с времяимпульсной модуляцией (ВИМ) ………………………………………………………. 2.6.1. Спектр сигнала с ВИМ-1 ……………………. 2.6.2. Спектр сигнала с ВИМ-2 …………………….. 3 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ …… 3.1. Структурная схема …………………………………. 3.2. Конструкция лабораторной установки …………… 4 ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ ……………………………………………………. 5 КОНТРОЛЬНЫЕ ВОПРОСЫ ………………………… 6 СПИСОК ЛИТЕРАТУРЫ …………………………….. |
3 3 3
6
9
13
15 16 18 18 20
20 21 24 24 24 26
27 28 29
31 33 34 |
1 Введение
Руководство к лабораторной работе содержит краткие теоретические сведения из теории спектрального анализа, описание лабораторной установки и методики эксперимента.
Цель работы – ознакомиться с некоторыми методами и схемами получения импульсно-модулированных сигналов и исследовать частотные спектры этих сигналов.
2 Некоторые сведения из теории
2.1 Понятие о спектре
Необходимость изучения спектров сигналов диктуется следующими причинами:
1) спектральный и временной подходы являются равноправными при анализе сигналов и систем;
2) изучение спектров сигналов позволяет правильно определить параметры и обоснованно предъявить требования к отдельным элементам системы;
3) обработка сигналов и, в частности, вопросы демодуляции предполагают хорошее знание их спектров;
4) в работе исследуются спектры сигналов при различных видах импульсной модуляции: амплитудно-импульсной (АИМ), широтно-импульсной (ШИМ) и времяимпульсной (ВИМ). Эти способы применяются для модуляции поднесущих колебаний в многоканальных системах передачи информации с временным разделением каналов.
Для
действительной функции
![]() (рис 2.1), определенной на интервале
(-∞;+∞)
и абсолютно интегрируемой
(рис 2.1), определенной на интервале
(-∞;+∞)
и абсолютно интегрируемой
|
(2.1) |
существует пара преобразований Фурье
|
(2.2) |
где
![]() – спектр функции
.
– спектр функции
.
Спектр является непрерывной функцией частоты и ограничен по величине (см. рис. 2.2).
Рис. 2.1 – Функция времени |
Рис. 2.2 – Модуль и фаза спектра функции |
Спектр есть комплексная функция. Так как – действительная функция времени, то из (2.2) непосредственно следует, что
|
(2.3) |
где
модуль
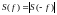 -
четная функция частоты, (В/Гц),
а
фаза
-
четная функция частоты, (В/Гц),
а
фаза
 – нечетная.
– нечетная.
Величина
 определяет не непосредственно амплитуду,
а спектральную плотность амплитуд.
Квадрат модуля амплитудного спектра
определяет не непосредственно амплитуду,
а спектральную плотность амплитуд.
Квадрат модуля амплитудного спектра
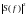 по физическому смыслу представляет
спектральную плотность мощности сигнала,
т.е. мощность сигнала на единицу полосы.
по физическому смыслу представляет
спектральную плотность мощности сигнала,
т.е. мощность сигнала на единицу полосы.
Прямоугольный импульс (рис.2.3) определяется формулой
|
(2.4) |
где
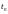 –
момент начала импульса;
–
момент начала импульса;
 – длительность
импульса;
– длительность
импульса;
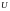 – амплитуда
импульса.
– амплитуда
импульса.
Воспользовавшись преобразованием Фурье (2.1), можно получить амплитудный спектр в виде
|
(2.5) |
На рис. 2.3 и 2.4 изображены прямоугольный импульс и модуль его спектра в области положительных частот.
Рис. 2.3 – Импульс прямоугольной формы |
Рис. 2.4 - Спектр импульса прямоугольной формы |
Амплитудный
спектр является непрерывной функцией
частоты и содержит составляющие во всём
интервале
(-∞<f<∞).
Для периодических функций интеграл
(2.2) расходится .
Это значит, что интеграл Фурье не применим
к периодическим сигналам.
.
Это значит, что интеграл Фурье не применим
к периодическим сигналам.
В [1] показано, что, воспользовавшись дельта-функцией δ(f), можно распространить преобразование Фурье и на периодические сигналы.
Пусть
|
(2.6) |
гармоническое колебание.
Подставляя (2.6) в (2.2), получим спектр
|
(2.7) |
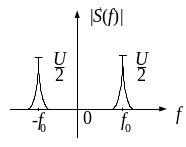
После простых преобразований окончательно спектр гармонического колебания может быть представлен в виде
|
(2.8) |
где
|
(2.9) |
интегральное выражение дельта-функции.
Как
следует из выражения (2.8), гармоническое
колебание имеет линейчатый спектр.
Распределение спектральной плотности
по частотам характеризуется сосредоточением
ее у двух значений частоты
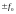 ,
и
плотность равна нулю при других значениях
частоты. Гармоническое колебание
,
и
плотность равна нулю при других значениях
частоты. Гармоническое колебание
 и его спектр представлены на рис. 2.5 и
2.6 соответственно.
и его спектр представлены на рис. 2.5 и
2.6 соответственно.
Рис. 2.5 – Гармоническое колебание |
Рис. 2.6 – Спектр гармонического колебания |



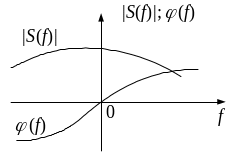
 ,
,