Задачи по ТиТпи

1. Частота квантования по времени равна F_к = 2 кГц. На вход подается гармонический сигнал частоты 400 Гц. Найти частоты еще хотя бы двух гармонических сигналов, которые дадут такую же последовательность отсчетов.

Два разных синусоидальных сигнала, неотличимых при квантовании: высокочастотный с частотой  f > f_к (красный) и низкочастотный  f < f_к (синий)

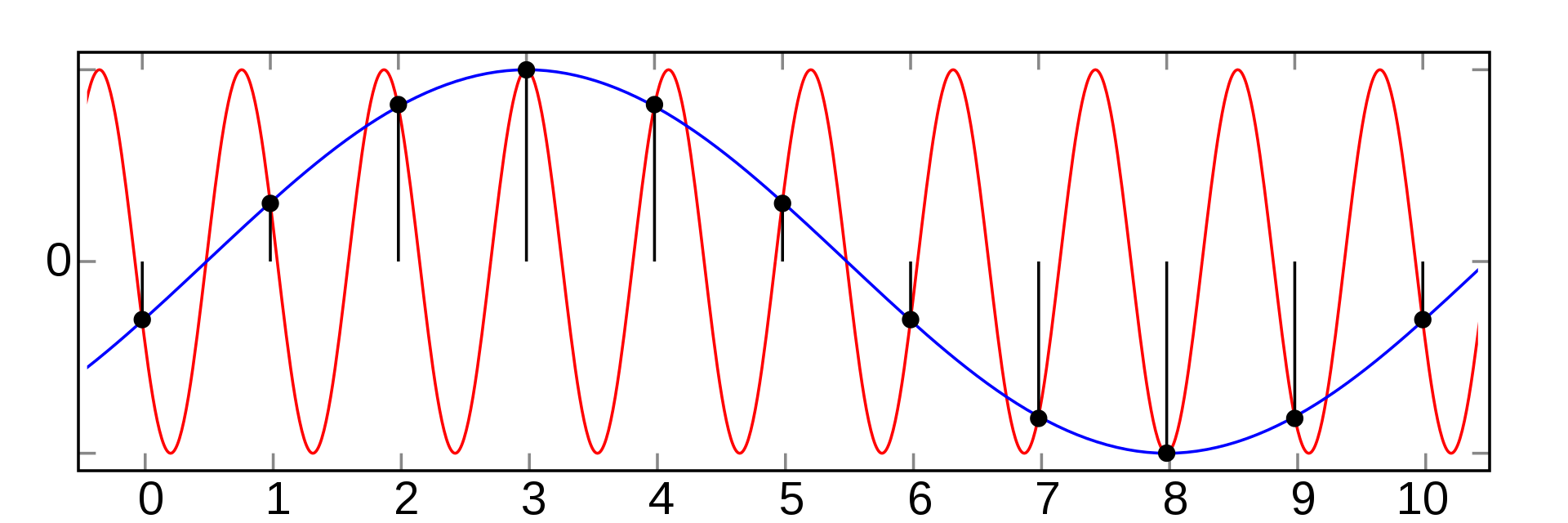
Δt = 0.5 мс F_в = F_к /2 = 1000 Гц u₁(t) = sin(2πf₁t) u₂(t) = sin(2πf₂t)

u₁(0) = u₂(0) = 0 u₁(Δt) = u₂(Δt) = sin(2πf₁Δt) = sin(2πf₂Δt)

0.951

2600 1600 4600

2. Пятиразрядный ацп рассчитан на диапазон входных напряжений 0 ... 8 в. Напряжение на входе 0,278 в. Найти двоичную комбинацию на его выходе.

7,1/0,25=

00001 0,25-0,5 0,375

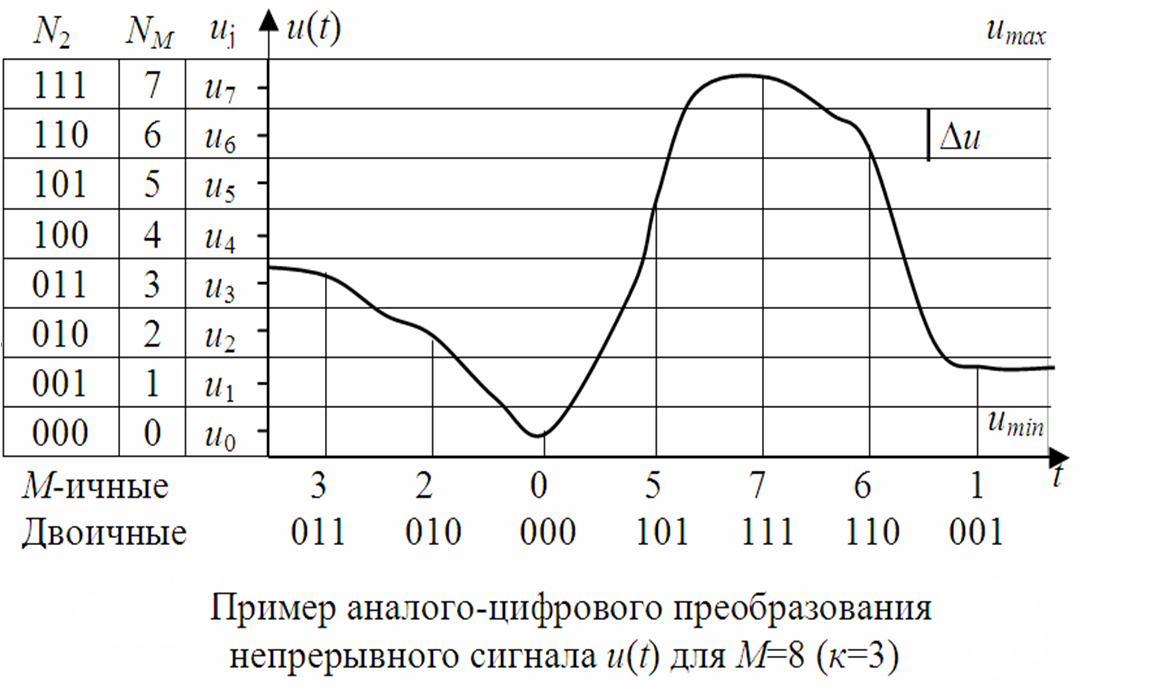
Δu = 8/32 = 0.25 шаг квантования по напряжению

Границы интервалов 0, 0.25. 0.5. 0.75. 8

Номера интервалов 00000, 00001, 00010, …, 11111.

7.278 29 7.278/0.25=

6.27 8 разрядов 200 11001000

3. Условия те же, но диапазон входных напряжений –4 ... 4 в.

17

4. На вход трансверсального цифрового фильтра второго порядка подается единичный отсчет. Найти числовую последовательность на его выходе, если g₀ = 1, g₁ = 0.9, g₂ = 0.5.

1 0.9 0.5 Коэффициенты

1 0 0 1

0 1 0 0.9

0 0 1 0.5

0 0 0 0

Вход Выход

5. На вход рекурсивного цифрового фильтра первого порядка подается единичный отсчет. Найти числовую последовательность на его выходе, если g₀ = 1, g₁ = –0.9.

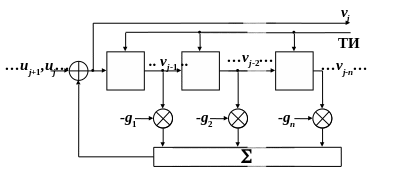
1 0,9 0,81 0,729

6. С передатчика ЦСПИ на вход изотропной (ненаправленной) передающей антенны поступает поток двоичных символов со скоростью 1 Мбит/с и средней мощностью 10 Вт. Длина радиолинии 100 км. Найти отношение сигнал-шум на входе приемника, если спектральная плотность мощности белого шума на его входе составляет N_o = 10^–18 Вт·с, а эффективная площадь приемной антенны равна 10 м².

7,95*10^-11 Вт/м² 7,95*10^-10 Вт 10^-12 Вт

10^–12 Вт 800 29 дБ 28

7. В условиях задачи 6 найти отношение сигнал-шум для минимального разностного сигнала при использовании: АМ; ЧМ; ФМ; КАМ-4; КАМ-16. При скорости 1 МБод/с.

8. Закодировать числовую последовательность 823568412567, используя метод контрольной суммы. Выяснить на примерах, какой кратности ошибки можно обнаруживать и исправлять (всегда или иногда) этим методом.

8235684125677

8. Решить задачу 8 для двоичной последовательности

0011. Считая, что передаваемая комбинация, это вектор-строка, записать в матричном виде основную операцию, выполняемую декодером. Привести несколько примеров, иллюстрирующих операции при кодировании и декодировании.

00110 00101 11110 00000 10100 01111 10001

10110

8. Составить кодовую таблицу (n = 3), записать производящую и проверочную матрицы для линейного блокового кода:

а) у которого максимальное количество комбинаций; (3,3) d=1

б) способного обнаруживать любую одиночную ошибку; (3,2) d=2

в) способного исправлять любую одиночную ошибку; (3,1)

г) способного обнаруживать любые одиночные и двукратные ошибки. (3,1)

В каждом случае найти минимальное расстояние Хэмминга между кодовыми комбинациями.

000 001 110 111 011 G = (111)

111 00011

0000 б) H=(111)

1111 1001 в) H=(110) б) G=101

101 10 011 100 101

а) G=100

101 11 010

001

011 001

101

110

111 100

011 010

101

110 111

111 110 000 010

011

101

110

(7,4) d = 3