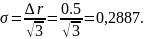1.3 Влияние помех в канале связи

Наличие шума и помех в двоичном канале приводит к ошибкам, которые проявляются в том, что некоторые двоичные символы изменяют свое значение на обратное.

Теоретически бесконечно большое последействие единичной ошибки связано с тем, что в амплитудном спектре единичного скачка S1(ω)=1/ω амплитуды составляющих бесконечно возрастают при   0. В целом результат воздействия некоррелированной помехи – это серия случайно возникающих скачков обеих полярностей, которая представляет собой дискретный случайный процесс с независимыми приращениями, который суммируется с полезным сигналом.

ДМ по своей сути не предназначена для передачи сигналов, содержащих постоянную составляющую, более того, реально она применяется для передачи сигналов, например речевых, спектр которых заключен в ограниченной полосе частот (ωн, ωв).

В качестве имитатора двоичного симметричного канала с независимыми ошибками в лабораторном макете используется сумматор по модулю 2, на один вход которого поступает передаваемая двоичная последовательность, а на другой вход – двоичная последовательность, имитирующая поток ошибок. Источником последней является генератор псевдослучайной M-последовательности с набором переключаемых схем совпадения, позволяющим изменять относительное количество единиц в потоке символов на втором входе сумматора по модулю 2.

2 Практическая часть

Подав на вход системы прямоугольные импульсы, были зарисованы осциллограммы в характерных точках, которые представлены на рисунках 2.1-2.8:

Рисунок 2.1 – Осциллограмма в точке A1

Рисунок 2.2 – Осциллограмма в точке А2

Рисунок 2.3 – Осциллограмма в точке А3

Рисунок 2.4 – Осциллограмма в точке А5

Рисунок 2.5 – Осциллограмма в точке Б1

Рисунок 2.6 – Осциллограмма в точке Б2

Рисунок 2.7 – Осциллограмма в точке Б4

Рисунок 2.8 – Осциллограмма в точке Б5

Зарисованные осциллограммы напряжений в характерных точках системы при нулевом входном напряжении, представлены на рисунках 2.9-2.16:

Рисунок 2.9 – Осциллограмма в точке A1 при нулевом напряжении

Рисунок 2.10 – Осциллограмма в точке A2 при нулевом напряжении

Рисунок 2.11 – Осциллограмма в точке A3 при нулевом напряжении

Рисунок 2.12 – Осциллограмма в точке A5 при нулевом напряжении

Рисунок 2.13 – Осциллограмма в точке Б1 при нулевом напряжении

Рисунок 2.14 – Осциллограмма в точке Б2 при нулевом напряжении

Рисунок 2.15 – Осциллограмма в точке Б4 при нулевом напряжении

Рисунок 2.16 – Осциллограмма в точке Б5 при нулевом напряжении

Сравним осциллограммы в характерных точках для прямоугольного импульса и при нулевом напряжении:

Таблица 2.1 – Сравнение осциллограмм

Характерная точка	Прямоугольные импульсы	Нулевое напряжение
А1	Наблюдаются прямоугольные импульсы	Отсутствие сигнала
А2	Виден сигнал	Отсутствие сигнала
А3	Наблюдаются импульсы	Наблюдаются импульсы
А5	Происходит дельта-модуляция	Происходит дельта-модуляция
Б1	Последовательность ошибок	Последовательность ошибок
Б2	Полезный сигнал с ошибками	Поток ошибок
Б4	Дельта-модуляция	Дельта-модуляция без сигнала
Б5	Сглаженный сигнал	Шум

Где:

А1 – входной сигнал;

А2 – выход компаратора;

A3 – выход генератора тактовых импульсов;

А5 – выход интегратора передатчика;

Б1 – выход имитатора потока ошибок;

Б2 – выход канала с ошибками;

Б4 – выход генератора приемника;

Б5 – выход ФНЧ приемника.

После чего измерили величины шага квантования по уровню и шага квантования по времени при нулевом входном напряжении. Согласно выставленным настройкам, одно деление по амплитуде составляет 0.5 В, а одно деление по времени – 0.2 мс.

Отсюда получим, что среднеквадратическая ошибка квантования по уровню (1.1):

После чего была снята амплитудно-частотная характеристика (АЧХ) системы связи без ФНЧ и зависимость коэффициента нелинейных искажений от частоты, результаты представлены в таблице 2.2.

Таблица 2.2 – Результаты измерений АЧХ и коэффициента нелинейных искажений

Частота f, Гц	Напряжение U, В	Коэффициент нелинейных искажений Кг, %
25	1,17	34%
50	1,2	31%
100	1,23	29%
200	1,2	30%
400	0,68	33%

Ниже на рисунке 2.17 представлена АЧХ системы связи без ФНЧ

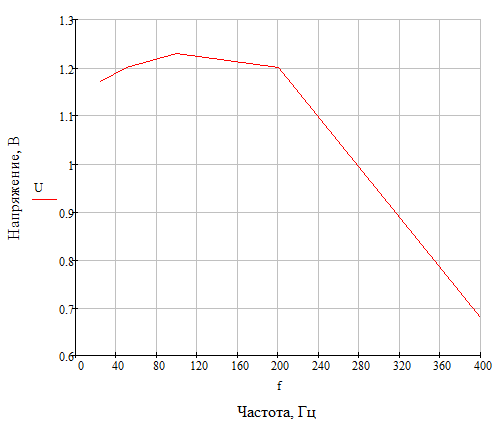
Рисунок 2.17 – АЧХ системы связи без ФНЧ

На рисунке 2.18 представлена зависимость коэффициента нелинейных искажений от частоты без ФНЧ

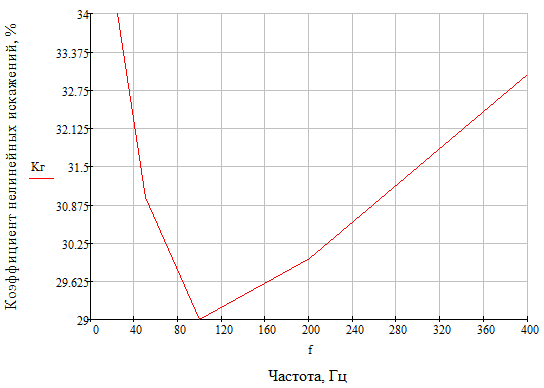
Рисунок 2.18 – Зависимость коэффициента нелинейных искажений от частоты без ФНЧ

Далее также снимем АЧХ и зависимость коэффициента нелинейных искажений от частоты с ФНЧ, , результаты представлены в таблице 2.3.

Таблица 2.3 – Результаты измерений АЧХ и коэффициента ошибок

Частота f, Гц	Напряжение U, В	Коэффициент нелинейных искажений Кг, %
25	1,23	14,5%
50	1,26	14%
100	1,35	13%
200	1,29	10,6%
400	0,27	11,5%

Ниже на рисунке 2.19 представлена АЧХ системы связи с ФНЧ

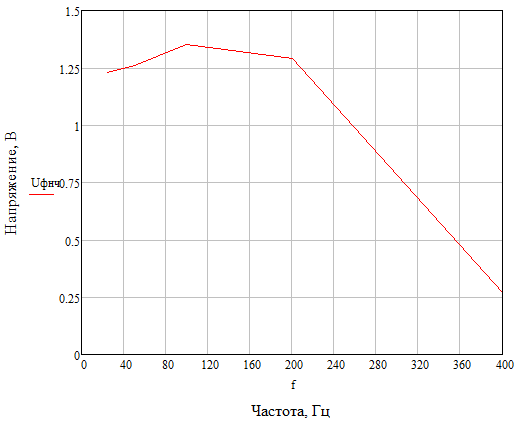
Рисунок 2.19 – АЧХ системы связи с ФНЧ

На рисунке 2.20 представлена зависимость коэффициента нелинейных искажений от частоты с ФНЧ

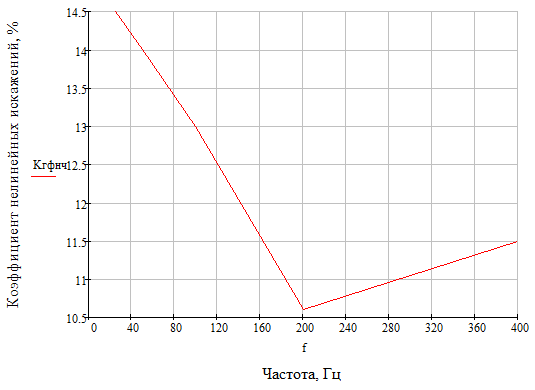
Рисунок 2.20 – Зависимость коэффициента нелинейных искажений от частоты с ФНЧ

Сравнивая зависимости коэффициентов нелинейных от частоты без ФНЧ (Рисунок 2.18) и с ФНЧ (Рисунок 2.20), можно увидеть, что значения Кг во втором случае меньше, чем в первом.