Методички и лекции / Laba_4_1B2-M_BarsKurPup

1 Введение

Целью лабораторной работы является:

1)Ознакомление с принципом ДМ;

2)Особенности построения систем связи с ДМ;

3)Исследование некоторых характеристик системы связи с дельта-

модуляцией.

2

2 Теоретическая часть

2.1 Принцип дельта-модуляции

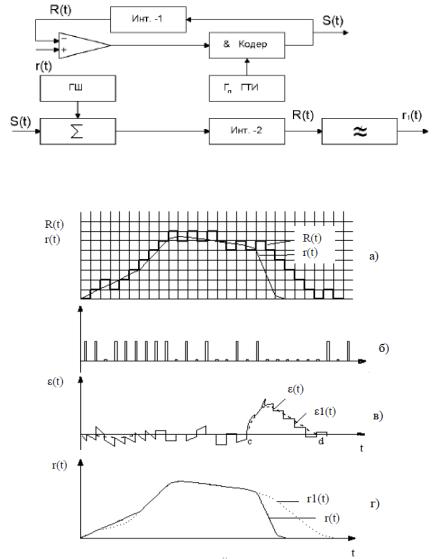
При ДМ передаётся не функция сообщения, а знак приращения функции сообщения. Принцип действия системы связи с применением ДМ можно пояснить функционально схемой (рисунок 2.1) и графиками напряжений в характерных точках, представленное на рисунке 2.2.

Рисунок 2.1 – Функциональная схема системы связи с ДМ

Рисунок 2.2 – Форма напряжений в характерных точках

Для наблюдения формы напряжения в контрольных точках (рисунок

2.1), предусмотрены следующие гнёзда для подключения осциллографа:

А1 – входной сигнал;

А2 – выход компаратора;

3

А3 – выход генератора тактовых импульсов;

А5 – выход интегратора передатчика;

Б1 – выход имитатора потока ошибок;

Б2 – выход канала с ошибками;

Б4 – выход генератора приёмника;

Б5 – выход ФНЧ приёмника.

Модулирующее напряжение ( ) и напряжение с выхода интегрирующего каскада ( ) подаются на два входа вычитающего устройства, то есть на выходе последнего имеем их разность ( ) = ( ) − ( ).

Генератор импульсов вырабатывает периодическую последовательность коротких тактовых импульсов, задающих тактовые моменты времени. Период следования этих импульсов определяет шаг квантования по времени ∆.

При подаче на вход кодирующего устройства k-го короткого тактового импульса в момент = ∆ оно вырабатывает прямоугольный импульс с фиксированными значениями амплитуды и длительности. Полярность этого импульса зависит только от знака разности ( ) в тактовый момент времени.

При (∆ ) ≤ 0, т.е. ( ∆ ) ≥ ( ∆ ), появляется положительный импульс;

иначе, при противоположных знаках равенства – импульс отрицателен.

Интегратор 1 выполняет математическую операцию интегрирования поступающих на его вход кодовых импульсов и работает по следующим правилам:

1)если с выхода кодирующего устройства на вход интегратора подаётся импульс положительной полярности, то напряжение на выходе интегратора скачком возрастает на величину ∆ и затем остаётся неизменным до прихода следующего импульса;

2)если с выхода кодирующего устройства на вход интегратора подаётся импульс отрицательной полярности, выходное напряжение

4

интегратора скачком уменьшается на ∆ и затем также остаётся неизменным до прихода следующего импульса.

Поскольку на выходе кодирующего устройства в тактовые моменты времени обязательно возникают импульсы той или иной полярности,

напряжение на выходе интегратора обязательно возрастает либо уменьшается на одну ступеньку и вследствие этого приобретает ступенчатую форму,

представленную на рисунке 2.2а. Величина ∆ определяет шаг квантования по амплитуде при таком аналого-цифровом преобразовании (АЦП) сигнала.

В каждом периоде тактовой частоты здесь передаётся информация только об одном из двух возможных перемещений ступенчатой кривой ( )

на одну ступеньку вверх или вниз. Таким образом, сигнал при дельта-

модуляции оказывается автоматически кодированным по двоичной системе и представляет собой импульсы всегда одинаковой величины, но различного знака. На практике обычно используют однополярное кодирование, то есть в тактовых точках импульс присутствует или имеется пауза, что соответствует положительным или отрицательным приращениям.

Функции декодирующего устройства на приёмной стороне выполняет интегратор 2, на выходе которого получается ступенчатое напряжение 1( ).

После его сглаживания фильтром нижних частот, получим функцию сообщения 1( ), близкую к ( ). Известно, что для уменьшения ошибок в передаче сообщений, интегратор 2 должен быть аналогичен интегратору 1.

2.2 Искажения при дельта-модуляции

Так как при ДМ сигнал подвергается квантованию по времени и по уровню, возникают принципиально неустранимые ошибки. Разность между аналоговым сигналом и напряжением аппроксимации называется сигналом ошибки 1( ) = ( ) − 1( ). Форма сигнала ошибки зависит как от передаваемого сигнала, так и от формы напряжения аппроксимации. В общем случае, чем выше тактовая частота, тем меньше успевает сигнал измениться за

5

время одного такта, т.е. чем меньше может быть выбрана ступенька квантования по уровню, тем точнее совпадают входной сигнал ( ) и его аппроксимация ( ), как представлено на рисунке 2.2а. Величина ошибки квантования определяется энергией сигнала ошибки, попадающей в полосу прозрачности ФНЧ-демодулятора. Характерной особенностью ошибок квантования является то, что они возникают лишь при непосредственной передаче сообщений, поэтому уровень помех при наличии полезного сигнала может быть больше уровня помех в его отсутствие.

Ошибки при передаче сообщений, обусловленные свойствами ДМ,

удобно рассматривать с учётом отдельных составляющих:

1)шумы квантования;

2)ошибки перегрузки по амплитуде;

3)ошибки перегрузки по скорости.

6

3 Результаты эксперимента

Подали сигнал, имитирующий передаваемое сообщение, на вход системы. Проверили работоспособность трёх видов входных сигналов,

соответствующих трём положениям переключателя «входной сигнал» (3 вида: «Внутренний П», «Внутренний ~», «Внешний»). Но не смогли добавить рисунки трёх видов входных сигналов, так как из-за высокой скорости мигания на осциллографе, при фотографировании исчезал сигнал, тем самым не могли выловить или зафиксировать на одном месте.

Включаем осциллограф на выход интегратора приёмной части системы

(гнездо Б4). Подаём на вход системы от генератора Г3-18 синусоидальное напряжение частоты 40-70 Гц. Устанавливаем амплитуду этого напряжения возможно большей величины, но так, чтобы ещё не наблюдались искажения перегрузки по напряжению. Полученный результат, представлен на осциллографе на рисунке 3.1.

Рисунок 3.1 – Осциллограф на выходе интегратора приёмной части системы

Сняли амплитудно-частотную характеристику системы связи без ФНЧ,

как представлено на рисунке 3.2, и зависимость коэффициента нелинейных искажений ( г) от частоты ( вхс), представленная на рисунке 3.3, и заносим в таблицу 3.1 полученные значения в каждый отсчёт по частоте.

7