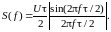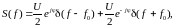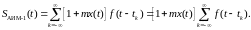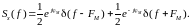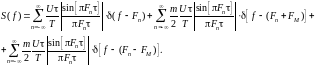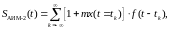Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра радиотехнических систем (РТС)

Исследование спектров импульсных модулированных сигналов

Отчёт по лабораторной работе по дисциплине

«Теория и техника передачи информации»

Выполнили:

студенты гр. 152-М

____________ В.А. Алтухов

____________ Д.О. Удовенко

«____» ______________ 2023 г.

Проверил:

Д.т.н., профессор каф. РТС

_______ __________ Ю.П. Акулинечев

^оценка «____» ______________ 2023 г.

Томск 2023

Введение

Необходимость изучения спектров сигналов диктуется следующими причинами:

1. спектральный и временной подходы являются равноправными при анализе сигналов и систем;

2. изучение спектров сигналов позволяет правильно определить параметры и обоснованно предъявить требования к отдельным элементам системы;

3. обработка сигналов и, в частности, вопросы демодуляции предполагают хорошее знание их спектров.

В работе исследуются спектры сигналов при различных видах импульсной модуляции: амплитудно-импульсной (АИМ), широтно-импульсной (ШИМ) и времяимпульсной (ВИМ). Эти способы предназначены для модуляции импульсных поднесущих в многоканальных системах передачи информации с временным разделением каналов.

Цель работы – ознакомиться с некоторыми методами и схемами получения импульсно-модулированных сигналов и исследовать частотные спектры этих сигналов.

1. Теоретическая часть

1. Спектры гармонических и импульсных сигналов

Воспользовавшись преобразованием Фурье, можно получить амплитудный спектр в виде:

(1.1)

На рисунке 1.1 изображены прямоугольный импульс и модуль его спектра в области положительных частот.

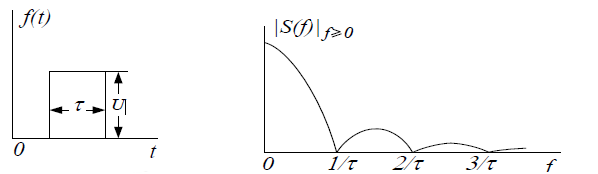
Рисунок 1.1 – Импульс прямоугольной формы и модуль ее спектра

Спектр гармонического колебания может быть представлен в виде:

(1.2)

где 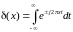– интегральное выражение δ-функции.

Как следует из выражения (1.2), гармоническое колебание имеет линейчатый спектр. Распределение спектральной плотности по частотам характеризуется сосредоточением ее у двух значений частоты ±f₀, и плотность равна нулю при других значениях частоты. Гармоническое колебание f(t) и его спектр представлены на рисунке 1.2 соответственно.

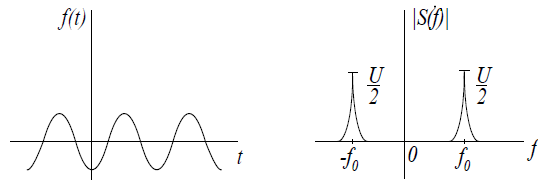
Рисунок 1.2 – Гармоническое колебание и модуль ее спектра

2. Спектр сигнала при амплитудно-импульсной модуляции

При АИМ-1 величина напряжения внутри импульса пропорциональна значению модулирующей функции x(t) в соответствующий момент времени:

(1.3)

Для последовательности прямоугольных импульсов, модулированных по закону АИМ-1 гармоническим колебанием вида 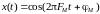со спектром:

(1.4)

После преобразований спектр будет описываться следующим выражением:

(1.5)

Последовательность прямоугольных импульсов с АИМ-1 и ее спектр приведены на рисунке 1.3.

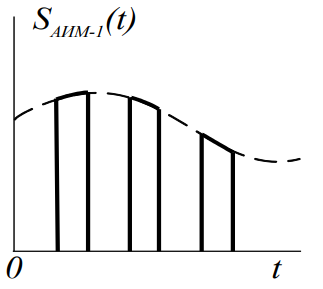
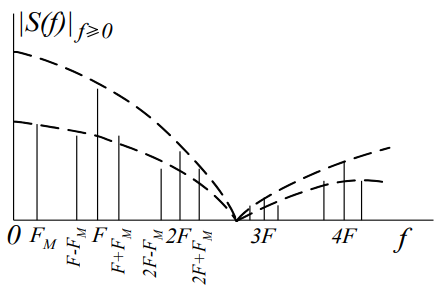
Рисунок 1.3 – Последовательность импульсов с АИМ-1

Демодуляция сигнала с АИМ-1 возможна:

1) полосовым фильтром

2) фильтром нижних частот (ФНЧ), и этот способ широко применяется.

При использовании реального ФНЧ (например, при аппроксимации частотной характеристики ФНЧ гауссовской кривой), коэффициент µ должен быть больше двух, практически он оказывается в пределах 3,0…3,5.

В случае АИМ-2 амплитуда импульса при модуляции изменяется пропорционально значению модулирующей функции в тактовые моменты времени.

Модулированная последовательность импульсов имеет вид:

(1.6)

где t_k = kT – тактовые моменты времени.

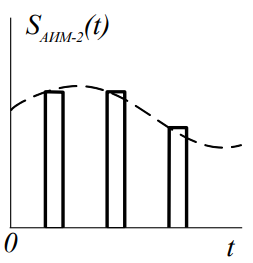
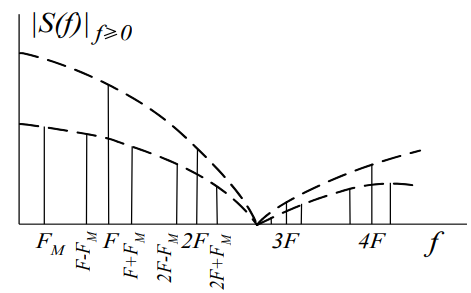
Рисунок 1.4 – Последовательность импульсов и ее спектр с АИМ-2

Величина искажений в спектре АИМ-2 зависит от отношения /T_M. Где T_M – период модулирующего напряжения. При /T_M→0 разница между АИМ-1 и АИМ-2 исчезает, и искажения отсутствуют. При увеличении /T_M искажения увеличиваются: это сказывается при демодуляции сигнала фильтром нижних частот.