Федеральное агентство по образованию РФ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

Акулиничев Ю.П.

КОДЫ С ПРОВЕРКАМИ НА ЧЕТНОСТЬ И ЦИКЛИЧЕСКИЕ КОДЫ

Учебно-методическое пособие к лабораторным исследованиям систем передачи информации

Томск, 2006

Федеральное агентство по образованию РФ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

Акулиничев Ю.П.

КОДЫ С ПРОВЕРКАМИ НА ЧЕТНОСТЬ И ЦИКЛИЧЕСКИЕ КОДЫ

Одобрено кафедрой радиотехнических систем в качестве учебно-методического пособия к лабораторным исследованиям для студентов специальностей:

071700 "Физика и техника оптической связи", 200700 “Радиотехника,” 201100 "Радиосвязь, радиовещание и телевидение", 201200 “Средства связи с подвижными объектами”, 201600 “Радиоэлектронные системы”, 201800 “Защищенные системы связи”.

СОДЕРЖАНИЕ

1. Введение ...................................................................................... 4

2. Сведения из теории корректирующих кодов ...................... 4

2.1. Общие сведения .................................................................... 4

2.2. Коды с проверками на четность .......................................... 5

2.3. Кодирование циклических кодов ........................................ 7

2.4. Декодирование циклических кодов .................................. 10

2.5. Обнаружение ошибок ......................................................... 11

2.6. Исправление ошибок .......................................................... 12

3. Оценка помехоустойчивости кода ....................................... 14

4. Лабораторная установка ....................................................... 15

5. Рекомендуемый порядок лабораторных исследований… 17

6. Контрольные вопросы ........................................................... 19

Литература ............................…………........................…........ 20

1. Введение

В цифровых системах связи широко применяются корректирующие коды, т.е. коды, способные обнаруживать и исправлять ошибки, возникающие в канале с шумом. Особенно часто используют коды с однократной проверкой на четность и циклические коды с кодовым расстоянием, равным трем.

Цель настоящей работы - изучение принципов построения кодера и декодера, а также экспериментальное исследование корректирующей способности кодов на примере кода с проверкой на четность (7,6) и циклического кода (7,4).

2. Сведения из теории корректирующих кодов

2. 1 . Общие сведения

В дискретных каналах с шумом передача символов сопровождается случайными ошибками. Основным способом повышения помехоустойчивости системы передачи информации (СПИ) в этих условиях является разумное введение избыточности в передаваемый сигнал.

Идея рационального введения избыточности в передаваемый сигнал реализуется применением корректирующих кодов. Наиболее часто применяют блочные корректирующие коды. Кодовая комбинация (КК) исходного безызбыточного кода (информационная, с выхода источника сообщений) содержит k разрядов

a_i= a₁, a₂,…, a_k,

где a_i=0;1. Будем рассматривать только двоичные коды (основание кода m=2). Число всех возможных КК от источника N=m^k=2^k. В пространстве двоичных КК вводят понятие расстояния Хэмминга. Расстоянием Хэмминга d_ij называет число символов, в которых кодовые комбинации a_i и a_j отличаются друг от друга. Для двоичного кода расстояние d_ij удобно определять как вес (количество единиц) кодовой комбинации, полученной в результате суммирования a_i и a_j по модулю два (mod 2). Суммирование по mod 2 выполняется по правилу

0Å0=0, 0Å1=1, 1Å0=1, 1Å1=0.

(2.1)

а вес КК есть число единиц в ней.

Для кодов, использующих в качестве разрешенных все N=2^k кодовых комбинаций, минимальное значение расстояния равно 1. Такие коды называют безызбыточными. Они не позволяют обнаруживать и исправлять ошибки, возникающие в канале связи. Для осуществления коррекции ошибок вводят избыточность:

1) в виде лишних, избыточных символов; тогда длина КК увеличивается и становится равной п=k+r. При этом избыточность кода оценивают как R=r/п;

2) выделением из общего числа N кодовых комбинаций N_p разрешенных, используемых для передачи. Остальные N_з=N-N_p являются запрещенными. Величина избыточности равна 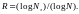Ошибки в канале связи обычно (но не обязательно) переводят разрешенную КК в запрещенную и таким образом обнаруживаются.

Отличие (расстояние) между переданной и принятой КК называют кратностью ошибки q. Корректирующие коды могут обнаруживать и (или) исправлять некоторые ошибки, возникающие при передаче по каналу связи. Для характеристики корректирующих свойств кода вводят понятие кодового расстояния, т.е. минимального расстояния Хэмминга для данного кода

dкод=min dij. i¹j

(2.2)

При грамотном введении избыточности в передаваемый сигнал минимальное расстояние увеличивается и становится d_код>l. Связь между кратностью обнаруживаемой ошибки q_o, кратностью исправляемой ошибки q_и и величиной кодового расстояния определяется так:

dкод³qo+1, dкод³2qи+1.

(2.3)

Таким образом, для обнаружения любой однократной ошибки (q_o=1) корректирующий код должен иметь d_код =2, а для исправления любой однократной ошибки (q_и=1) нужно иметь d_код =3.