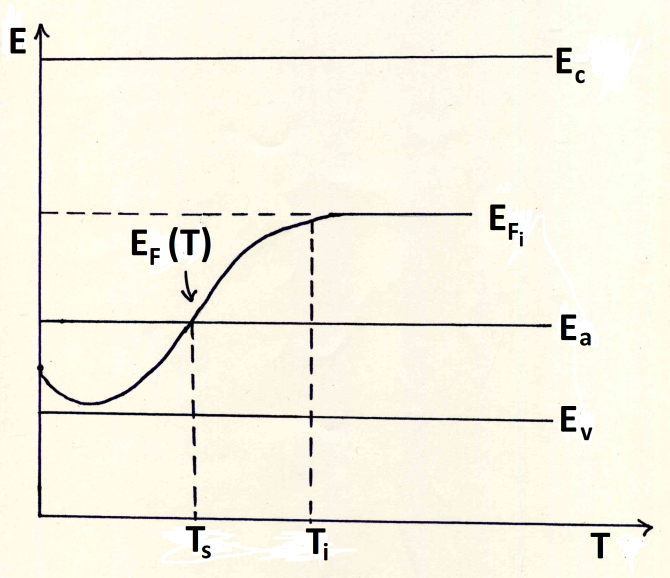
5.2. Акцепторный полупроводник

Формулы для энергии Ферми и концентрации носителей в полупроводниках p-типа получают аналогично. Они имеют тот же вид, что и для донорных полупроводников, если сделать замену N_c → N_v, E_ud → E_ua, E_c–E_F → E_F–E_v. Зависимость E_F(T), будет выглядеть следующим образом:

Зависимость lnp=f(1/T) совершенно аналогична кривой lnn=f(1/T) для донорного полупроводника.

5.3. Закон действующих масс

Как для собственных, так и для примесных невырожденных полупроводников произведение концентраций электронов и дырок есть постоянная величина, не зависящая от степени легирования:

Формула

называется законом действующих масс. Произведение концентрации электронов и дырок в полупроводнике не зависит от степени его легирования (N_d или N_а), а зависит только от температуры. Оно равно квадрату концентрации электронов (или дырок ) в собственном полупроводнике.

Из закона действующих масс следует, что в примесных полупроводниках в области примесной проводимости концентрация неосновных носителей (дырок – в донорном полупроводнике) оказывается намного меньше, чем в собственном полупроводнике. Это на примере n-полупроводника объясняется следующим образом. Установление равновесной концентрации определяется не только генерацией носителей, то есть тепловым возбуждением электронов с донорных уровней, но и их рекомбинацией. Когда в зоне проводимости появляется большое число электронов с донорных уровней, освобожденные уровни в валентной зоне гораздо быстрее занимаются электронами, чем в собственном полупроводнике, что приводит к резкому уменьшению концентрации дырок.

Отметим, что закон действующих масс справедлив только для невырожденных полупроводников.

5.4. Сильно легированные полупроводники

С увеличением степени легировании, кривая lnn от 1/T в областях примесной проводимости смещается параллельно вверх (см. формулу (10)). Так же параллельно вверх смещается зависимость lnn от 1/T в области истощения примеси, где n не зависит от температуры (в зоне плато).

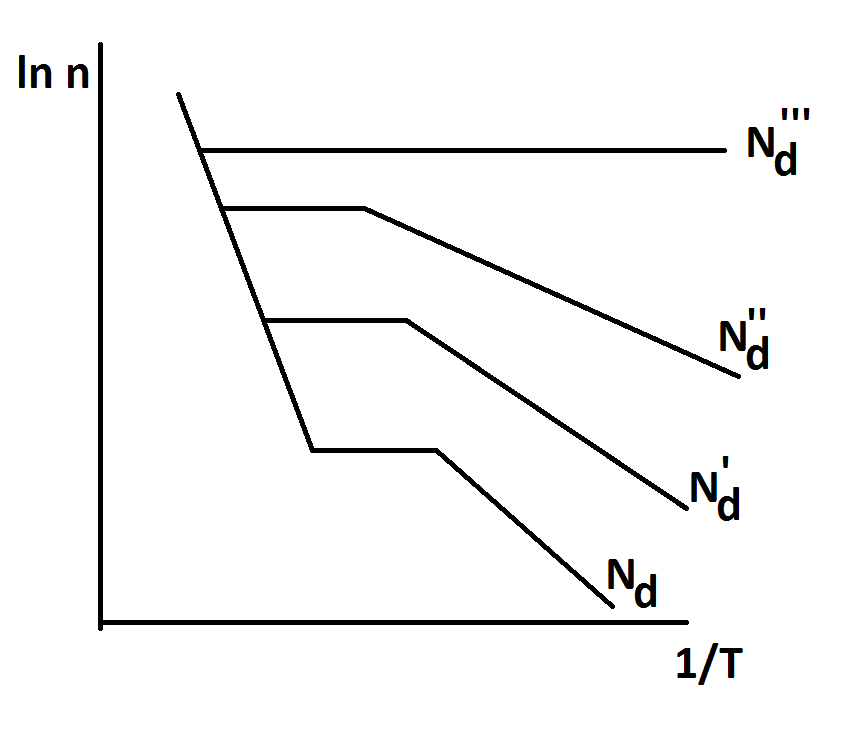
После достижения некоторого значения N_d, наклон зависимости начинает уменьшаться ( ), а затем и вообще становится равным нулю ( ). Уменьшение наклона начинается тогда, когда волновые функции электронов на соседних примесях начинают перекрываться, и вместо локальных уровней примеси, возникает примесная энергетическая зона. В этом случае запрещенная зона – щель между примесной зоной и зоной проводимости (валентной зоной для p-полупроводника) уменьшается по ширине. Поэтому наклон прямой lnn(1/T) уменьшается, поскольку уменьшается энергия ионизации примеси Е_иd. Наконец, при еще большей концентрации примеси примесная зона сливается с зоной проводимости (с валентной зоной для p-полупроводника), энергия ионизации примеси становится равной нулю (Е_иd = 0) и наклон зависимости lnn(1/T) (или lnp(1/T)) становится нулевым.

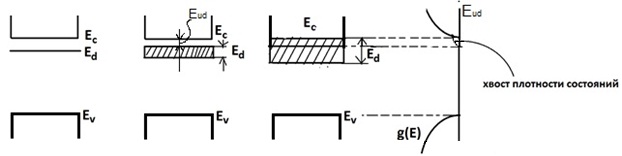
На рисунке справа приведена зависимость плотности состояний g(E) при слиянии примесной зоны и зоны проводимости. Образуется хвост плотности состояний.

Отметим, что из-за большого радиуса электронных орбит “лишних” электронов примесный уровень размывается в зону при сравнительно больших межпримесных расстояниях.

В сильнолегированных полупроводниках электронный газ является вырожденным. Однако и в сильнолегированных полупроводниках при приближении к температуре T_i уровень Ферми переходит в запрещенную зону, в результате чего электронный газ становится так же, как и в слаболегированных полупроводниках, невырожденным.