- •Физическая электроника Введение
- •Тема: Основы зонной теории твердых тел
- •1. Зоны разрешенных значений энергии в кристалле
- •2. Заполнение зон электронами и деление тел на металлы, диэлектрики и полупроводники
- •2.1. Число состояний в зоне
- •2.2. Связь заполнения зон с электрическими свойствами твердых тел
- •2.3. Поведение электронов во внешнем электрическом поле
- •3. Собственные полупроводники
- •4. Локальные уровни в запрещенной зоне
- •4.1. Донорные уровни
- •4.2. Акцепторные уровни
- •Тема: Статистика электронов и дырок в полупроводниках и металлах
- •1. Функция распределения в статистике Ферми-Дирака:
- •Функцию плотности состояний
- •Функцию распределения
- •2. Функция плотности состояний
- •3. Концентрация электронов и дырок в полупроводнике
- •3.1. Концентрация электронов в полупроводнике
- •3.2. Концентрация дырок в полупроводнике
- •4. Положение уровня Ферми и концентрация свободных носителей заряда в собственных полупроводниках
- •5. Статистика электронов в примесных полупроводниках
- •5.1. Донорный полупроводник
- •5.2. Акцепторный полупроводник
- •5.3. Закон действующих масс
- •5.4. Сильно легированные полупроводники
- •5.5. Компенсированные полупроводники
- •6. Статистика электронов в металлах
- •Тема: Неравновесные носители заряда в полупроводниках
- •1. Равновесные и неравновесные носители заряда (определение)
- •2. Время жизни. Скорости генерации и рекомбинации
- •3. Уравнение непрерывности
- •Диффузия и дрейф неравновесных носителей
- •4.1. Введение
- •4.2. Эффективный коэффициент диффузии
- •4.3. Стационарное распределение неравновесных носителей за слоем генерации
- •4.4. Максвелловское время релаксации
- •Тема: Электронная эмиссия Введение
- •1. Поверхностный потенциальный барьер для электронов в металле (Работа выхода)
- •2. Формула для плотности тока термоэлектронной эмиссии (Формула Ричардсона-Дешмена)
- •В ывод формулы для тока насыщения
- •3. Эффект Шоттки
- •4. Автоэлектронная эмиссия
- •5. Фотоэлектронная эмиссия
- •5.1. Основные закономерности. Формула Эйнштейна для фотоэффекта
- •5.2. Фотоэлектронная эмиссия из металлов
- •5.3. Фотоэлектронная эмиссия из диэлектриков и полупроводников
- •6. Вторичная электронная эмиссия
- •Тема: Электронные лампы
- •Двухэлектродные вакуумные лампы (диоды)
- •Вольт-амперная характеристика (вах) диода
- •Параметры диодов
- •Трехэлектродные лампы (триоды)
- •Внутреннее уравнение лампы
- •Недостатки триодов
- •Тетроды и пентоды
- •Тема. Электрический ток в газах
- •1. Ионизация газов. Упругие и неупругие столкновения
- •2. Длина свободного пробега. Эффективное сечение взаимодействия
- •3. Скорости генерации и рекомбинации
- •Несамостоятельный разряд в газе
- •5. Экспериментальное определение коэффициента рекомбинации
- •6. Распределение электронов по длинам свободного пробега
- •7. Лавинный разряд. Явление усиления тока при наличии ионизирующего соударения
- •8. Самостоятельный разряд
- •8.1. Лавинный разряд при объемной ионизации электронами и гамма-процессах на катоде
- •8.2. Зажигание самостоятельного разряда
- •8.2.1. Условия зажигания самостоятельного разряда
- •8.2.2. Процесс развития самостоятельного разряда
- •8.2.3. Развитие и установление самостоятельного разряда
- •8.2.4. Напряжение зажигания самостоятельного разряда
- •8.3. Формы самостоятельного разряда
- •8.3.1. Тлеющий разряд
- •8.3.2. Дуговой разряд
- •8.3.3. Коронный разряд
- •8.3.4. Искровой разряд
- •Тема: Движение электрона в электрических и магнитных полях
- •Электронная оптика
- •Движение электрона в однородном электрическом поле
- •3. Электростатическая электронная линза
- •1) Линзы-диафрагмы
- •2) Бипотенциальные линзы
- •3) Одиночные линзы
- •4. Магнитные линзы
- •Тема: Электронная микроскопия
- •Устройство электронного микроскопа
- •2. Разрешающая способность и увеличение электронного микроскопа
1. Функция распределения в статистике Ферми-Дирака:
Пусть dN – число частиц в интервале энергий dЕ, тогда:
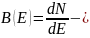 (1)
(1)
полная функция распределения.
Введем в рассмотрение еще две функции:
Функцию плотности состояний
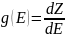 ,
,
где dZ – число состояний, приходящихся на интервал энергий dE, и
Функцию распределения
 ,
,
имеющую смысл вероятности заполнения состояний.
Тогда с учетом (1) получим связь между B(E), g(E) и f(E):
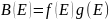 .
.
Для фермионов – частиц с полуцелым спином, в том числе электронов, функция распределения f(E) имеет вид:
 (2)
(2)
и называется
функцией
Ферми-Дирака.
В формуле (2)
 – химический потенциал системы,
называемый иначе уровнем
или энергией Ферми.
– химический потенциал системы,
называемый иначе уровнем
или энергией Ферми.
При Т=0: f(E)=1 для E<EF и f(E)=0 для E>EF:

Это означает, что при Т = 0 все состояния с E<EF заняты электронами, а состояния с E > EF свободны. Другими словами, при Т = 0 электроны занимают все наинизшие энергетические уровни в интервале от 0 до EF.
При Т > 0 из
выражения (1) для значения энергии, равной
энергии Ферми (E
= EF),
имеем
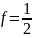 .
Таким образом, при температуре, отличной
от абсолютно нуля, уровень
Ферми есть энергетический уровень,
вероятность заполнения которого
равна 1/2.
.
Таким образом, при температуре, отличной
от абсолютно нуля, уровень
Ферми есть энергетический уровень,
вероятность заполнения которого
равна 1/2.
С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни, и характер их распределения по состояниям меняется. Тепловому возбуждению подвергаются электроны лишь узкой полосы kT у уровня Ферми, а электроны более глубоких уровней остаются практически незатронутыми, так как энергии kT теплового движения недостаточно для их возбуждения. За счет такого возбуждения часть электронов с энергией, меньшей EF, переходит на уровни с энергией, большей EF. В результате устанавливается новое распределение частиц по состояниям:

Повышение температуры вызывает размытие распределения на глубину kT как с той, так и с другой стороны от энергии EF и появление «хвоста» распределения справа от EF. Чем выше температура, тем больше kT и тем более существенные изменения происходят в функции распределения.
Для электронов,
находящихся в состояниях с энергией
 ,
выражение для f(E)
принимает вид:
,
выражение для f(E)
принимает вид:
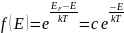 .
.
где
 .
Эта функция совпадает с функцией
распределения Максвелла-Больцмана для
частиц, подчиняющихся классическим
законам (статистике Больцмана).
.
Эта функция совпадает с функцией
распределения Максвелла-Больцмана для
частиц, подчиняющихся классическим
законам (статистике Больцмана).
Определение: Если
электроны подчиняются статистике
Больцмана, то их состояния называются
невырожденным
электронным газом.
Характерной особенностью невырожденного
электронного газа является то,
что
 .
.
2. Функция плотности состояний
Функция плотности
состояний
обычно рассчитывается, исходя из
упрощенного представления о том, что
энергия в кристалле зависит только от
модуля волнового вектора
.
Эти расчеты дают для
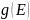
в зоне проводимости:
 ,
,
где
– масса электрона у дна зоны проводимости,
V
– объем кристалла,
 ,
,
в валентной зоне:
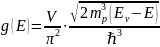 ,
,
где
 – масса дырки у потолка валентной зоны,
– масса дырки у потолка валентной зоны,
 .
.