5. Экспериментальное определение коэффициента рекомбинации

После выключения ионизатора и источника питания имеем

. (3)

Откуда, интегрируя найденное из (3) дифференциальное уравнение

с начальными и конечными условиями: n, n₀, t, 0, получаем

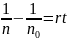. (4)

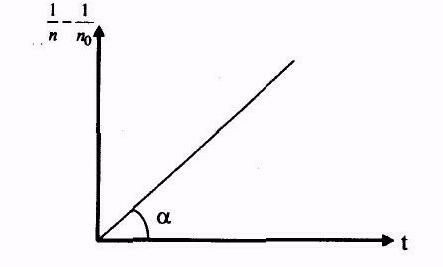
Согласно (4) тангенс угла наклона этой зависимости равен искомому коэффициенту рекомбинации r.

6. Распределение электронов по длинам свободного пробега

Формула для определяет среднюю длину свободного пробега. Результат же каждого конкретного столкновения электрона с атомом зависит от фактической длины свободного пробега, которая принимает различные значения.

Для определения вероятности различных длин свободного пробега предположим, что в момент времени t=0 из поверхности с координатой х=0 в направлении оси х вылетело n₀ электронов. Продолжая свое движение на пути dх, часть электронов сталкивается с частицами газа и число нестолкнувшихся частиц на пути dх уменьшается на dn.

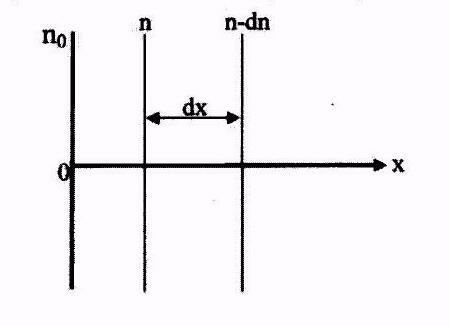
Так как в среднем одна частица на единице пути испытывает столкновений, то на пути dх этих столкновений будет 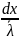и убыль нестолкнувшихся частиц составит

.

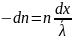Знак «минус» здесь соответствует убыли электронов. Решением этого уравнения является:

.

Это выражение определяет вероятность того, что фактическая длина свободного пробега будет больше х (относительное число тех электронов, чья длина свободного пробега больше х).

Функция

есть функция распределения длин свободного пробега: вероятность того, что длина свободного пробега заключена в пределах 0 – х. Другими словами, это есть относительное число электронов, чья длина свободного пробега меньше х.

7. Лавинный разряд. Явление усиления тока при наличии ионизирующего соударения

Наиболее активными частицами по отношению к ионизирующей способности атомов являются электроны (а не ионы и нейтральные атомы). Это объясняется тем, что при электронном ударе на неупругий процесс может идти вся кинетическая энергия, в то время как при соударении атомов (или иона и атома) приблизительно одинаковой массы на ионизацию (или на возбуждение) может идти только половина кинетической энергии. Кроме того, у электрона и длина свободного пробега больше в раза, чем у атома или иона.

Подсчитаем, как будет изменяться ток в газовом промежутке, в котором ионизирующие соударения производятся только электронами.

Пусть один электрон (первичный электрон), вышедший из катода и движущийся в электрическом поле ε, порождает α пар зарядов на единице пути. Величину α называют коэффициентом ударной ионизации. Электроны, создаваемые первичным электроном, ускоряются и сами становятся способными ионизировать атомы газа. Предположим, что все вторичные электроны так же принимают участие в ионизации.

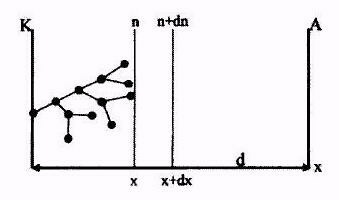
Если расстояние между катодом (К) и анодом (А) d больше нескольких 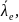то каждый электрон на пути dх претерпевает αdх ионизирующих столкновений. Тогда прирост электронов dn (на пути dх) будет равен

, (1)

где п(х) - число электронов, прошедших через сечение х за единицу времени.

После интегрирования уравнения (1) с граничными условиями:

получаем

усиленный поток – хорошо известную экспоненциальную зависимость.

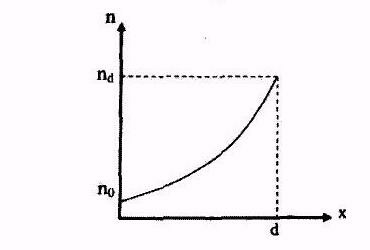
Соответственно, плотность тока электронов на аноде будет равна

Таким образом, в результате мы получили, что число электронов увеличивается в раз – один электрон порождает лавину электронов в количестве, равном .

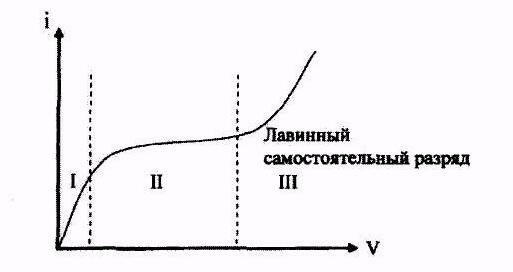
Исследуем теперь зависимость величины α от напряженности электрического поля ε и давления газа р.

Предположим, что при каждом столкновении электрон теряет свою скорость полностью и после столкновения начинает ускоряться (в поле ε) заново. Чтобы электрон мог ионизовать газ, он должен на пути свободного пробега х приобрести энергию хеε, не меньшую энергии ионизации, то есть

xeε ≥ eV_i (V_i – потенциал ионизации)

или

xε ≥ V_i. (4)

Из условия равенства (4) находим минимальный свободный пробег ионизации x_i:

.

Покажем, что все электроны с х ≥ x_i (набравшие необходимую энергию) ионизуют атомы при соударении. Возьмем пучок из n₀ электронов, которые начали двигаться в электрическом поле ε. В результате теплового движения и движения в электрическом поле электроны имеют свободные пробеги как большие, так и малые. Электроны, у которых λ_e ≥ x_i будут производить ионизацию, а у которых λ_e < x_i, ионизации производить не будут.

Возьмем формулу для распределения электронов по длинам свободного пробега

, (5)

которая показывает, какое число из первоначальных n₀ электронов имеет пробег, больший х. Если в (5) взять х = х_i, то все такие электроны будут ионизировать газ:

.

На пути в 1 см (на единице пути) один электрон испытывает в среднем

столкновений. На этом же пути электронов испытают k = nz столкновений и так же вызовут ионизацию

. (7)

Число ионизаций, производимых на том же (единичном) пути одним электроном, будет равно

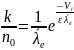. (8)

Это есть не что иное, как коэффициент ударной ионизации 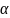. Итак, это

(9)

Поскольку

то

, (10)

где

Тогда выражение для коэффициента ударной ионизации α перепишется в виде

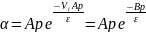, (12)

где

B = V_iA. (13)

Выражение (12) для α обычно записывают в виде:

, (14)

то есть

(15)

Зависимость 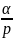от подтверждается экспериментально. Она показывает, что величина зависит от р и не по отдельности, а от их отношения . То есть, если изменять р и так, чтобы отношение не изменялось, то и величина не изменится.

Физически зависимость 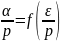объясняется следующим образом. Допустим, что и р увеличены от и р₁ до и р₂ таким образом, что отношение к р не изменяется:

.

Согласно (10) свободный пробег , а вместе с ним и минимальный свободный пробег ионизации х_i, уменьшаются в раз. В то же время, энергия х_iе , приобретаемая на этих пробегах, остается прежней, так как напряженность поля увеличивается во столько же, а именно, в раз.