Тема: Электронная эмиссия Введение

Электронная эмиссия – это эмиссия или выход электронов из твердых или жидких тел.

Процессы эмиссии распадаются на 4 основных типа:

1. Термоэлектронная эмиссия – выход электронов при высокой температуре.

2. Холодная эмиссия (автоэлектронная эмиссия) – выход электронов вследствие туннельного эффекта.

3. Фотоэлектронная эмиссия – эмиссия, вызываемая поглощением электронами электромагнитного излучения.

4. Вторичная электронная эмиссия – выход электронов при бомбардировке потоком электронов или других частиц.

1. Поверхностный потенциальный барьер для электронов в металле (Работа выхода)

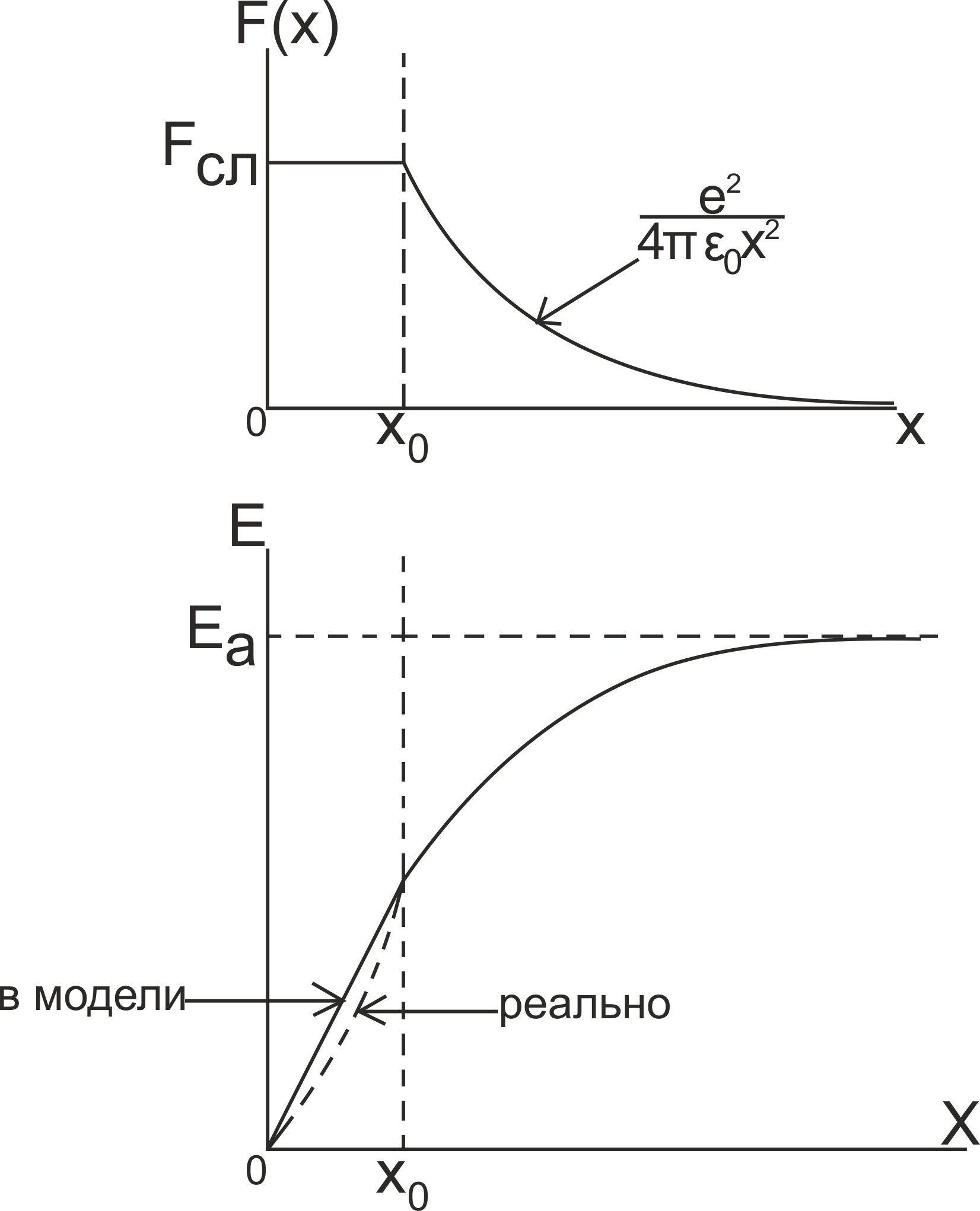
x₀ – межатомное расстояние.

В модели:

1. Внутри двойного электрического слоя существует однородное электрическое поле Ɛ (от 0 до x₀) и действует постоянная сила F_сл=Ɛe.

2. За слоем действует сила электрического изображения F_i:

.

Считаем, что на границе слоя в точке х₀ сила изображения F_i без скачка (см. рисунок) переходит в силу двойного электрического слоя:

.

Рассчитаем работу выхода E_a – работу, совершаемую электроном при удалении его с поверхности металла в бесконечность. E_a – это работа, совершаемая против 1) силы двойного слоя и 2) силы электрического изображения :

.

.

Итак, мы получили, что работа выхода равна

.

Из этой формулы следует, что чем меньше межатомное расстояние, тем больше работа выхода.

2. Формула для плотности тока термоэлектронной эмиссии (Формула Ричардсона-Дешмена)

Эффект насыщения тока, протекающего через вакуумный диод, открыл Эдиссон в 1883 году.

Формулу для тока насыщения дали Ричардсон в 1901 году и уточнил Дешмен в 1923 году.

В ывод формулы для тока насыщения

Расчеты проведем в предположении, что объем кристалла V=1 (!).

Число квантовых состояний dZ внутри элемента объема импульсного пространства с учетом спина электрона и с учетом того, что элементарный объем (объем, приходящийся на одно состояние) равен , есть:

.

Число электронов в этом элементе объема с учетом распределения Ферми-Дирака равно:

.

Для электронов, эмиттированных из металла, выполняется условие . Поэтому

,

где учтено, что:

.

Направим ось x перпендикулярно к поверхности металла. Найдем долю электронов , x-составляющая импульса которых заключена между p_x и p_x+dp_x. Для этого последнее выражение для dN проинтегрируем по p_z и p_y от –∞ до +∞:

.

Используя интеграл ( ), получаем:

.

Плотность потока электронов, подходящих (!) к поверхности и имеющих импульс в пределах от до , есть:

.

Плотность потока электронов, выходящих (!) с единицы поверхности, определяется электронами, имеющими энергию E > E_a (E_a – высота поверхностного потенциального барьера). Она равна интегралу:

,

где , а Ф = – работа выхода.

Наконец, плотность тока (тока насыщения) определяется произведением заряда электрона е и плотности потока L_x:

,

где

.

Эта формула носит название формулы Ричардсона-Дешмена.