
- •Описание метода и установки
- •1.Как различаются полупроводники, металлы и изоляторы по электропроводности? Какова зонная структура изолятора, проводника и полупроводника?
- •4. Объясните механизм собственной и примесной проводимостей у полупроводников.
- •5. Что такое подвижность носителей заряда и как она зависит от температуры в полупроводниках?
- •6. Объясните физический смысл энергий активации Eg и Eпр и температурного коэффициента сопротивления . Как они находятся экспериментально.
- •7. Почему температурный коэффициент сопротивления для полупроводников дается в справочниках для определенного температурного интервала?
МИНОБРНАУКИ РОССИИ
«Челябинский государственный университет»
(ФГБОУ ВО «ЧелГУ»)
Физический факультет
Кафедра радиофизики и электроники
ЛАБОРАТОРНАЯ РАБОТА № 7
ТЕМА: ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ
СОПРОТИВЛЕНИЯ ПОЛУПРОВОДНИКОВ И ОПРЕДЕЛЕНИЕ ЭНЕРГИИ АКТИВАЦИИ
Выполнил: Агеев А.А.
Группа: ФФ-304
Принял: Чернов В.М.
Челябинск
2025
ЦЕЛЬ РАБОТЫ: исследование физических свойств, характеристик и параметров терморезисторов; определение энергии активации примеси и ширины запрещенной зоны полупроводников.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: полупроводниковый терморезистор, нагревательная печь, тиристорный регулятор напряжения, мультиметр типа С1-107, ртутный термометр.
ТЕОРИЯ
К
полупроводникам относятся вещества,
занимающие по электропроводности
промежуточное положение между проводниками
(металлами) и диэлектриками. Основным
признаком, выделяющим полупроводники
как особый класс веществ, является
сильное влияние температуры и концентрации
примесей на их электрическую проводимость.
У большинства полупроводников сильное
изменение электрической проводимости
возникает под действием света, ионизирующих
излучений и других энергетических
воздействий. Таким образом, полупроводник
- это вещество, удельная проводимость
которого существенно зависит от внешних
факторов. Применяемые в электронике
полупроводники имеют монокристаллическую
структуру, в которой атомы размещены в
строго периодической последовательности,
образуя кристаллическую решетку. В
идеальной кристаллической решетке (без
примесей и без колебаний атомов) все
электроны связаны со своими атомами,
поэтому такая структура не проводит
электрический ток. Однако в полупроводниках
сравнительно небольшие энергетические
воздействия могут привести к отрыву
некоторых электронов от своих атомов.
Такие освобожденные от валентной связи
электроны обладают способностью
перемещаться по кристаллической решетке.
Их называют электронами проводимости.
Энергетические состояния электронов
проводимости образуют целую зону уровней
энергии, называемую зоной проводимости.
В интервале значений энергии от
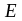 до
+
до
+
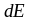 число энергетических уровней, на которых
могут находиться электроны проводимости,
равно
число энергетических уровней, на которых
могут находиться электроны проводимости,
равно
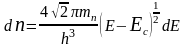 ,
(1)
,
(1)
где
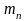 - эффективная масса электрона проводимости,
Ес
- минимальный уровень энергии электрона
(дно) зоны проводимости,
- эффективная масса электрона проводимости,
Ес
- минимальный уровень энергии электрона
(дно) зоны проводимости,
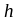 - постоянная Планка.
- постоянная Планка.
В соответствии с принципом Паули в одном и том же энергетическом состоянии могут находиться два электрона, имеющие различные ориентации спина.
Энергетические
состояния валентных электронов также
образуют зону уровней энергии, называемую
валентной. Максимальный уровень энергии
(потолок) этой зоны обозначим
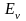 (рис. 1а).
(рис. 1а).
При
разрыве валентной связи и уходе электрона
из атома в кристаллической решетке
образуется незаполненная связь - дырка,
которой присущ нескомпенсированный
положительный заряд, численно равный
заряду электрона
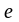 .
На незаполненную связь легко переходят
валентные электроны с соседних связей,
чему способствует тепловое движение в
кристалле. Поэтому дырка хаотически
перемещается по решетке. При наличии
внешнего электрического поля дырка
будет двигаться в направлении, определяемом
вектором напряженности поля, что
соответствует перемещению положительного
заряда, то есть возникнет электрический
ток.
.
На незаполненную связь легко переходят
валентные электроны с соседних связей,
чему способствует тепловое движение в
кристалле. Поэтому дырка хаотически
перемещается по решетке. При наличии
внешнего электрического поля дырка
будет двигаться в направлении, определяемом
вектором напряженности поля, что
соответствует перемещению положительного
заряда, то есть возникнет электрический
ток.
 Между
максимальным уровнем энергии валентной
зоны E
и
минимальным уровнем энергии зоны
проводимости
Между
максимальным уровнем энергии валентной
зоны E
и
минимальным уровнем энергии зоны
проводимости
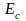 лежит область энергетических состояний,
в которой электроны не могут находиться.
Эта зона называется запрещенной
(рис. 1а). Ширина запрещенной зоны
лежит область энергетических состояний,
в которой электроны не могут находиться.
Эта зона называется запрещенной
(рис. 1а). Ширина запрещенной зоны
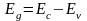 определяет
минимальную порцию энергии, необходимую
для освобождения валентного электрона,
то есть энергию активации (ионизации)
атома полупроводника. У германия
определяет
минимальную порцию энергии, необходимую
для освобождения валентного электрона,
то есть энергию активации (ионизации)
атома полупроводника. У германия
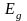 =
0,66 эВ, у кремния 1,08 эВ, у арcенида
галлия 1,41 эВ.
=
0,66 эВ, у кремния 1,08 эВ, у арcенида
галлия 1,41 эВ.
Полупроводники, имеющие в узлах кристаллической решетки только свои атомы, называют собственными полупроводниками. В электронике часто применяют полупроводники, у которых часть атомов основного вещества в узлах решетки замещена атомами другого вещества. Такие полупроводники называют примесными. Для германия и кремния чаще всего используют пятивалентные (фосфор, сурьма, мышьяк) и трехвалентные (бор, алюминий, галлий) примеси.
При
наличии пятивалентной примеси четыре
валентных электрона примесного атома
совместно с четырьмя электронами
соседних атомов образуют ковалентные
связи и полностью укомплектовывают все
восемь орбиталей валентной оболочки
примесного атома. При этом пятому
электрону валентной оболочки примеси
уже нет места на этой оболочке. Между
ним и положительным ионом примеси теперь
находятся сильно поляризующиеся
электронные облака валентных связей.
Поэтому связь этого электрона с ионом
примеси сильно ослабляется. В соответствии
с этим энергия связи этого электрона с
ином примеси
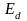 намного меньше энергии Еg.
Поэтому пятый электрон при комнатной
температуре и даже более низких
температурах может быть оторван от
своего атома за счет энергии теплового
движения. В этом случае образуется
электрон и неподвижный положительный
заряд - атом примеси, потерявший этот
электрон. Такие примеси, отдающие
электроны, называют донорными.
намного меньше энергии Еg.
Поэтому пятый электрон при комнатной
температуре и даже более низких
температурах может быть оторван от
своего атома за счет энергии теплового
движения. В этом случае образуется
электрон и неподвижный положительный
заряд - атом примеси, потерявший этот
электрон. Такие примеси, отдающие
электроны, называют донорными.
При наличии трехвалентной примеси примесный атом отдает три своих валентных электрона для образования ковалентных связей c тремя близлежащими атомами. Незаполненная связь с четвертым атомом без потери энергии заполняется электроном соседних связей. В результате примесный атом с присоединенным “лишним“ электроном образует в кристаллической решетке неподвижный отрицательный заряд, и, кроме того, образуется дырка, энергия связи которой Ea с центральным отрицательно заряженным ионом примеси снова оказывается сильно ослабленной из-за поляризации электронов валентной оболочки. Такие дырки уже при не очень высоких температурах сравнительно легко могут быть оторваны от иона акцептора и после этого свободно перемещаться по кристаллической решетке. Примеси, захватывающие электроны, называют акцепторными.
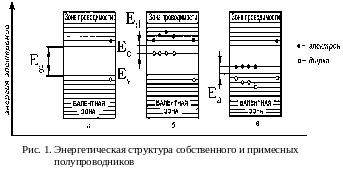
На
энергетической диаграмме полупроводника
(рис. 1) донорные и акцепторные примеси
образуют локальные энергетические
уровни, лежащие в запрещенной зоне.
Уровни доноров находятся около дна зоны
проводимости, их энергия активации
равна
,
а уровни акцепторов - у потолка валентной
зоны, их энергия ионизации равна
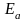 (рис. 1б, 1в).
(рис. 1б, 1в).
Вероятность
нахождения
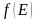 свободного электрона в энергетическом
состоянии
свободного электрона в энергетическом
состоянии
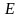 определяется статистической функцией
Ферми-Дирака
определяется статистической функцией
Ферми-Дирака
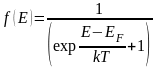 ,
(2)
,
(2)
где
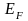 - энергия, которой электрон обладает с
вероятностью
- энергия, которой электрон обладает с
вероятностью
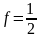 (уровень Ферми). Из (I)
и (2) можно определить концентрацию
электронов проводимости для
собственного полупроводника, определяющую
его проводимость
(уровень Ферми). Из (I)
и (2) можно определить концентрацию
электронов проводимости для
собственного полупроводника, определяющую
его проводимость

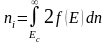 .
.
При
умеренных температурах, когда
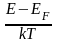 >>1
(невырожденный полупроводник)
>>1
(невырожденный полупроводник)
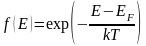 .
(3)
.
(3)
Концентрация электронов проводимости для собственного полупроводника равна
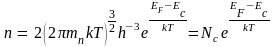 .
(4)
.
(4)
Аналогично вычисляется концентрация дырок для собственного полупроводника
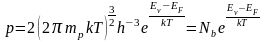 ,
(5)
,
(5)
где
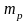 -
эффективная масса дырки.
-
эффективная масса дырки.
Определим собственную концентрацию носителей заряда
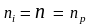 ,
(6)
,
(6)
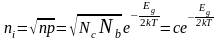 .
(7)
.
(7)
Концентрация
электронов проводимости при не слишком
высоких температурах
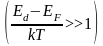 в примесном донорном полупроводнике
определяется выражением
в примесном донорном полупроводнике
определяется выражением
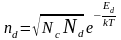 ,
(8)
,
(8)
где
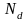 - концентрация донорной примеси.
- концентрация донорной примеси.
Аналогичные
расчеты для концентрации дырок при
условии
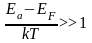 в примесном акцепторном полупроводнике
дают
в примесном акцепторном полупроводнике
дают
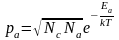 ,
(9)
,
(9)
где
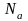 - концентрация акцепторной примеси.
- концентрация акцепторной примеси.
При
нарушении условия
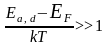 в примесном полупроводнике наблюдается
истощение примеси, когда в донорном
полупроводнике все электроны доноров
переходят в зону проводимости и nd=Nd,
или в акцепторном полупроводнике все
дырки акцепторов переходят в валентную
зону. Температурная зависимость в этом
случае отсутствует.
в примесном полупроводнике наблюдается
истощение примеси, когда в донорном
полупроводнике все электроны доноров
переходят в зону проводимости и nd=Nd,
или в акцепторном полупроводнике все
дырки акцепторов переходят в валентную
зону. Температурная зависимость в этом
случае отсутствует.
При более высоких температурах происходит термическая генерация пар электрон-дырка. В этом случае проводимость превращается из примесной в собственную.
Если
в полупроводнике одновременно имеются
как донорные, так и акцепторные примеси,
то концентрация носителей заряда
определяется отношением этих примесей.
Для концентрации электронов (при
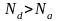 )
и дырок (при
)
и дырок (при
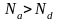 )
в случае низких температур можно записать
)
в случае низких температур можно записать
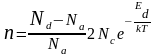 (10)
(10)
и
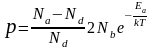 .
(11)
.
(11)
Электроны и дырки в кристалле находятся в состоянии хаотического теплового движения. При наличии электрического поля на это хаотическое движение носителей заряда накладывается компонента направленного движения. В результате электроны и дырки начинают перемещаться вдоль кристалла - возникает электрический ток, который называется дрейфовым током.
Вследствие
теплового движения атомов и наличия
дефектов кристаллической решетки
происходит рассеяние электронов и дырок
при столкновении с дефектом и колеблющимся
атомом. В результате электрон и дырка
не ускоряются неограниченно, как в
вакууме, а движутся с определенной
скоростью. Средние добавочные скорости
всей совокупности электронов и дырок
полупроводника, вызванные действием
сил поля
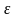 с учетом статистического распределения
временных интервалов свободного пробега
электрона и дырки, равны
с учетом статистического распределения
временных интервалов свободного пробега
электрона и дырки, равны
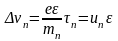 ,
(12)
,
(12)
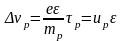 ,
(13)
,
(13)
где
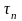 ,
- соответственно среднее время свободного
пробега электрона и дырок;
,
- соответственно среднее время свободного
пробега электрона и дырок;
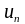 ,
,
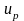 - соответственно, подвижности электронов
и дырок.
- соответственно, подвижности электронов
и дырок.
При рассеянии носителей заряда на тепловых колебаниях решетки
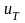 ~
~
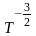 ,
(14)
,
(14)
а при рассеянии на ионах примесей
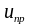 ~
~
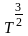 .
(15)
.
(15)
Последний механизм рассеяния преобладает над первым при низких температурах. Если же в рассеянии участвуют оба рассмотренных механизма рассеяния, то температурная зависимость подвижности носителей может быть представлена соотношением вида
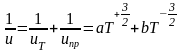 .
(16)
.
(16)
Электропроводность полупроводника определяется как концентрацией, так и подвижностью носителей заряда. Так, для собственного полупроводника удельная электропроводность равна
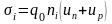 .
(17)
.
(17)
Учитывая зависимость концентрации и подвижности носителей заряда от температуры (см. формулы (7) и (14)), удельную электропроводность собственного полупроводника можно записать в виде
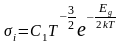 .
(18)
.
(18)
Множитель
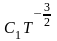 медленно меняется с температурой, тогда
как второй множитель
медленно меняется с температурой, тогда
как второй множитель
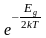 сильно зависит от температуры (если
сильно зависит от температуры (если
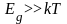 ).
Следовательно, для не слишком высоких
температур можно считать, что
).
Следовательно, для не слишком высоких
температур можно считать, что
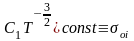 ,
,
и выражение для удельной электропроводности собственного полупроводника заменить более простым
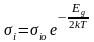 .
(19)
.
(19)
В примесном полупроводнике при достаточно высоких температурах проводимость полупроводника является собственной, а при низких температурах примесной. В области низких температур для удельной электропроводности примесной проводимости можно записать:
для примесного полупроводника с одним типом примеси
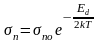 ,
(20)
,
(20)
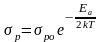 ,
(21)
,
(21)
для
примесного полупроводника с акцепторной
и донорной примесями
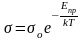 ,
(22)
,
(22)
где
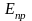 - энергия активации примесного
полупроводника.
- энергия активации примесного
полупроводника.
В области истощения примеси концентрация основных носителей остается постоянной и проводимость изменяется за счет изменения подвижности носителей. Если основным механизмом рассеяния носителей в области истощения примеси является рассеяние на тепловых колебаниях решетки, то проводимость уменьшается с ростом температуры. Если же основным механизмом рассеяния является рассеяние на ионизированных примесях, то проводимость будет увеличиваться с ростом температуры.
Описание метода и установки
Теплоэлектрический полупроводниковый прибор, использующий зависимость проводимости (сопротивления) полупроводника от температуры, предназначенный для регистрации изменения температуры окружающей среды, называется терморезистором или термистором. Материалами для изготовления терморезисторов служат оксиды различных металлов: меди, марганца, цинка и т.д. Область применения каждого типа терморезистора определяется его свойствами и параметрами: температурной характеристикой и коэффициентом сопротивления.
Зависимость проводимости полупроводникового материала от температуры называется температурной характеристикой. В данной работе для снятия температурной характеристики исследуемый полупроводниковый терморезистор помещен в нагревательную печь - трубчатый резистор. На одном уровне с ним находится ртутная головка термометра. В эксперименте измеряется сопротивление терморезистора с помощью мультиметра типа CI-I07.
Температура
исследуемого образца определяется
величиной протекающего через трубчатый
резистор электрического тока, задаваемого
с помощью тиристорного регулятора
напряжения. Измерения проводят через
каждые 10 градусов от комнатной температуры
до 300°С, плавно изменяя напряжение. По
полученным значениям вычисляют
проводимость
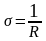 и строят графики
и строят графики
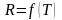 ,
,
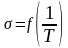 и
и
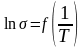 ,
где
,
где
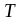 –
температура по шкале Кельвина.
–
температура по шкале Кельвина.
В данном полупроводниковом терморезисторе в исследуемом интервале температур в измеряемые значения сопротивления (и проводимости) подвижности носителей вносят пренебрежимо малый вклад. Поэтому сопротивление терморезистора определяется только примесной и собственной проводимостями. В соответствии с этим обстоятельством проводимость представляет собой сумму двух экспонент
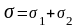 ,
(23)
,
(23)
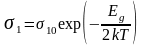 ,
,
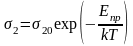 ,
(23а)
,
(23а)
где
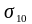 и
и
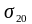 -
условные собственная и примесная
проводимости при
-
условные собственная и примесная
проводимости при
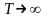 .
Для того, чтобы определить энергии
активации
.
Для того, чтобы определить энергии
активации
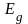 и
и
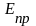 ,
необходимо разделить экспоненты.
Поскольку
,
необходимо разделить экспоненты.
Поскольку
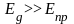 ,
то при больших значениях
,
то при больших значениях
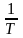 (низких
температурах) вклад в
(низких
температурах) вклад в
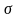 обусловлен практически только второй
экспонентной в (23) -
обусловлен практически только второй
экспонентной в (23) -
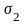 .
В зависимости
эта экспонента представляет собой
прямую линию со стороны больших значений
(рис.2). Наклон этой прямой определяется
энергией активации
.
В зависимости
эта экспонента представляет собой
прямую линию со стороны больших значений
(рис.2). Наклон этой прямой определяется
энергией активации
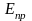 .
Энергия
вычисляется по формуле
.
Энергия
вычисляется по формуле
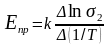 ,
(24)
,
(24)
где
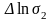 приращение, полученное при изменении
обратной температуры на
приращение, полученное при изменении
обратной температуры на
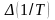 (см. рис.2).
(см. рис.2).
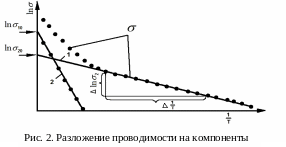 Для
выделения другой компоненты проводимости
Для
выделения другой компоненты проводимости
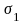 необходимо продолжить прямую линию
(прямую I
на рис.2), проходящую через точки при
больших значениях
(малых значениях температуры), в сторону
малых значений обратной температуры.
Эта линия соответствует второй экспоненте
в (23). Для выделения первой компоненты
теперь надо из результирующей зависимости
вычесть
.
необходимо продолжить прямую линию
(прямую I
на рис.2), проходящую через точки при
больших значениях
(малых значениях температуры), в сторону
малых значений обратной температуры.
Эта линия соответствует второй экспоненте
в (23). Для выделения первой компоненты
теперь надо из результирующей зависимости
вычесть
.
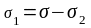 .
(25)
.
(25)
Построив
зависимость
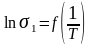 (прямая 2 на рис. 2), вычисляют энергию
активации
(прямая 2 на рис. 2), вычисляют энергию
активации
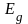 .
.
Температурный
коэффициент сопротивления
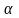 показывает относительное изменение
абсолютной величины сопротивления при
изменении температуры на 1K
и определяется формулой
показывает относительное изменение
абсолютной величины сопротивления при
изменении температуры на 1K
и определяется формулой
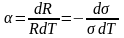 (26)
(26)
При низких температурах (при больших 1/Т), когда проводимость полупроводника определяется наличием примеси, первым слагаемым в (23) можно пренебречь и
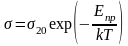 ,
(27)
,
(27)
или
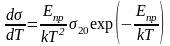 ,
(28)
,
(28)
Подставляя (28) и (27) в (26), получим
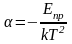 .
(29)
.
(29)
Таким
образом, при низких температурах для
прямолинейного участка зависимости
значение коэффициента
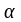 может быть вычислено по формуле (29).
может быть вычислено по формуле (29).
