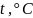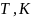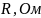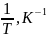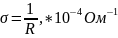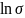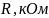Обработка результатов.
|
Нагрев |
|
Охлаждение |
|
|
|
|
|
|
|
|||||||
40 |
10,12 |
310 |
0,126 |
313 |
5123 |
0,0032 |
1,95 |
-8,541 |
50 |
8,3 |
300 |
0,154 |
323 |
4227 |
0,0031 |
2,37 |
-8,349 |
60 |
6,92 |
290 |
0,172 |
333 |
3546 |
0,0030 |
2,82 |
-8,174 |
70 |
5,88 |
280 |
0,205 |
343 |
3042,5 |
0,0029 |
3,29 |
-8,020 |
80 |
4,92 |
270 |
0,24 |
353 |
2580 |
0,0028 |
3,88 |
-7,856 |
90 |
4,08 |
260 |
0,281 |
363 |
2180,5 |
0,0028 |
4,59 |
-7,687 |
100 |
3,41 |
250 |
0,306 |
373 |
1858 |
0,0027 |
5,38 |
-7,527 |
110 |
2,87 |
240 |
0,378 |
383 |
1624 |
0,0026 |
6,16 |
-7,393 |
120 |
2,39 |
230 |
0,438 |
393 |
1414 |
0,0025 |
7,07 |
-7,254 |
130 |
1,879 |
220 |
0,506 |
403 |
1192,5 |
0,0025 |
8,39 |
-7,084 |
140 |
1,68 |
210 |
0,597 |
413 |
1138,5 |
0,0024 |
8,78 |
-7,037 |
150 |
1,396 |
200 |
0,69 |
423 |
1043 |
0,0024 |
9,59 |
-6,950 |
160 |
1,197 |
190 |
0,815 |
433 |
1006 |
0,0023 |
9,94 |
-6,914 |
170 |
1,041 |
180 |
0,955 |
443 |
998 |
0,0023 |
1,00 |
-6,906 |
180 |
0,863 |
170 |
1,12 |
453 |
991,5 |
0,0022 |
1,01 |
-6,899 |
190 |
0,734 |
160 |
1,296 |
463 |
1015 |
0,0022 |
9,85 |
-6,923 |
200 |
0,652 |
150 |
1,525 |
473 |
1088,5 |
0,0021 |
9,19 |
-6,993 |
210 |
0,557 |
140 |
1,806 |
483 |
1181,5 |
0,0021 |
8,46 |
-7,075 |
220 |
0,473 |
130 |
2,23 |
493 |
1351,5 |
0,0020 |
7,40 |
-7,209 |
230 |
0,409 |
120 |
2,63 |
503 |
1519,5 |
0,0020 |
6,58 |
-7,326 |
240 |
0,356 |
110 |
3,12 |
513 |
1738 |
0,0019 |
5,75 |
-7,460 |
250 |
0,306 |
100 |
3,76 |
523 |
2033 |
0,0019 |
4,92 |
-7,617 |
260 |
0,263 |
90 |
4,46 |
533 |
2361,5 |
0,0019 |
4,23 |
-7,767 |
270 |
0,227 |
80 |
5,37 |
543 |
2798,5 |
0,0018 |
3,57 |
-7,937 |
280 |
0,195 |
70 |
6,39 |
553 |
3292,5 |
0,0018 |
3,04 |
-8,099 |
290 |
0,168 |
60 |
7,68 |
563 |
3924 |
0,0018 |
2,55 |
-8,275 |
300 |
0,146 |
50 |
9,3 |
573 |
4723 |
0,0017 |
2,12 |
-8,460 |
310 |
0,126 |
40 |
11,22 |
583 |
5673 |
0,0017 |
1,76 |
-8,643 |
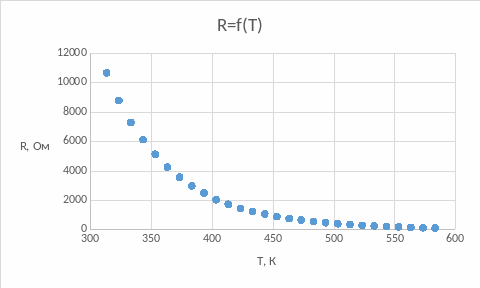
График зависимости R = f(T)
График
зависимости
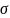= f(1/T)
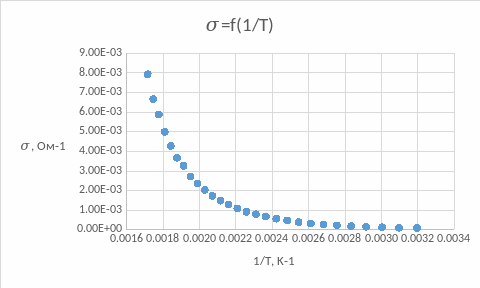
График зависимости ln = f(1/T)
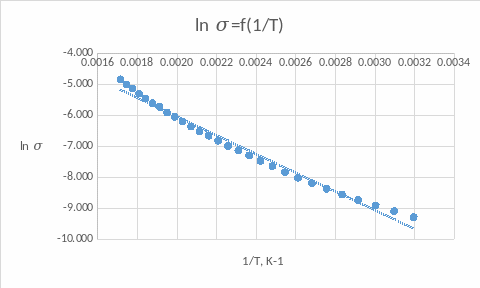
По углу наклона прямой методом наименьших квадратов находим Епр:
Приводим
зависимость
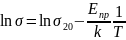к виду
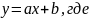
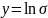
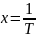
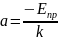
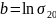
В результате расчетов по МНК:
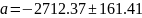
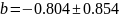
Тогда:
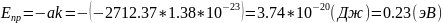
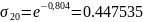
По углу наклона прямой методом наименьших квадратов находим Еg:
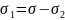
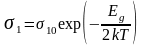
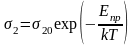
Приводим
зависимость
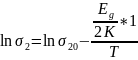к виду y=a+bx,
где:
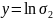
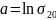
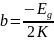
Метод МНК:
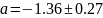
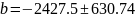
Отсюда:
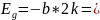
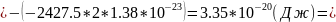
0.21
(эВ)
В формуле ошибка, должно быть сигма 1 и 10. После пересчета должно получиться 1,46 эВ
Добавим данные к зависимости ln :
-
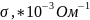
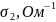
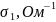
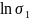
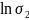
503
2,36
0,00204
0,0003
-8,036
-6,196
513
2,72
0,00226
0,0005
-7,682
-6,091
523
3,27
0,00250
0,0008
-7,177
-5,990
533
3,68
0,00276
0,0009
-6,995
-5,892
543
4,28
0,00303
0,0013
-6,684
-5,799
553
5,00
0,00332
0,0017
-6,388
-5,708
563
5,88
0,00362
0,0023
-6,091
-5,621
Здесь непоследовательно написана таблица, надо исправить. Поменять местами два столбца. (по последовательности расчетов)
Дополненный график:
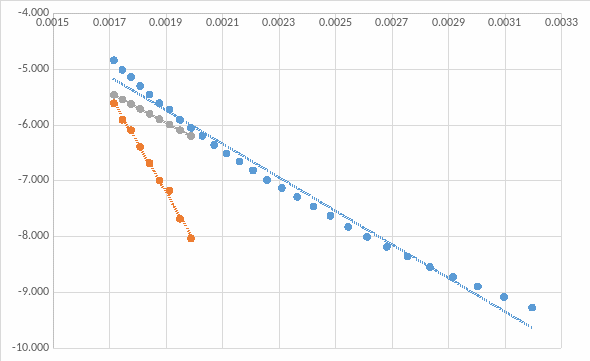
В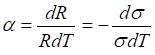
ычислим
температурный коэффициент сопротивления
:
-
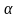α1
αпримес
-0,0213
-0,0268
-0,0205
-0,0251
-0,0190
-0,0237
-0,0192
-0,0223
-0,0205
-0,0211
-0,0191
-0,0199
-0,0197
-0,0189
-0,0193
-0,0179
-0,0222
-0,0170
-0,0179
-0,0162
График зависимости:
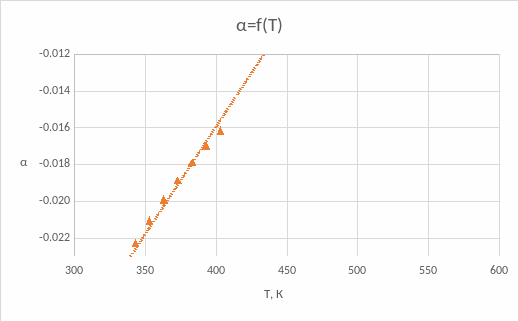
Вывод: исследованы физические свойства, характеристики и параметры терморезисторов, определены энергии активации примеси и ширина запрещенной зоны полупроводников.
Сняты значения сопротивления R при определенной температуре при нагреве и охлаждении. Построены графики зависимостей R = f(T), = f(1/T) и ln = f(1/T).
По методу наименьших квадратов определены:
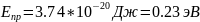
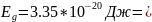0.21
эВ
Вычислен температурный коэффициент сопротивления α.
Построен график зависимости α = f(T).