
МИНОБРНАУКИ РОССИИ
«Челябинский государственный университет»
(ФГБОУ ВО «ЧелГУ»)
Физический факультет
Кафедра радиофизики и электроники
ЛАБОРАТОРНАЯ РАБОТА № 4
ТЕМА: РАСПРЕДЕЛЕНИЕ ТЕРМОЭЛЕКТРОНОВ ПО СКОРОСТЯМ
Выполнил: Агеев А.А.
Группа: ФФ-304
Принял: Чернов В.М.
Челябинск
2025
Цель работы: получение экспериментальной зависимости распределения электронов по скоростям, определение температуры катода.
Приборы и принадлежности: лабораторная установка с диодом 6Х6С, источниками накала и анодного напряжения, универсальный вольтметр В7-21А для измерения тока накала, универсальный вольтметр В7-21А для измерения анодного тока, мультиметр ВР-11А для измерения анодного напряжения.
Общие сведения
В вакуумных и газонаполненных приборах находит широкое применение явление термоэлектронной эмиссии. Термоэлектронной эмиссией называется явление эмиссии (выхода) электронов из нагретых тел. В настоящее время перспективными являются приборы миллиметрового диапазона с высокой плотностью тока эмиссии, вакуумные интегральные схемы, содержащие автоэлектронный катод или термокатод. Свойства эмиттера во многом определяют характеристики всего прибора. В частности, шумовые характеристики связаны с распределением электронов по скоростям.
Распределение электронов по энергиям внутри металла описывается статистикой ФермиДирака:
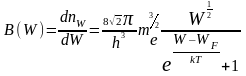 ,
(1)
,
(1)
где
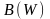
полная функция распределения электронов
по энергиям;
полная функция распределения электронов
по энергиям;
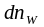 число
электронов в единице объема, имеющих
при температуре Т
энергию в интервале от W
до
число
электронов в единице объема, имеющих
при температуре Т
энергию в интервале от W
до
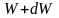 ;
;
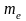 масса
электрона;
масса
электрона;
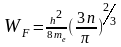 энергия
Ферми (n
концентрация электронов в металле).
энергия
Ферми (n
концентрация электронов в металле).
График распределения электронов по энергиям в металле показан на рис.1 (кривая слева).
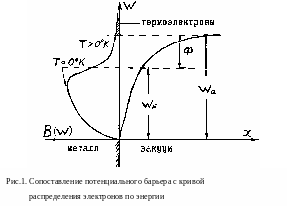 Электроны,
свободно перемещающиеся внутри металла,
не могут выйти за его пределы без затраты
энергии, так как вблизи поверхности
существует потенциальный барьер,
препятствующий
их
вылету.
График потенциального барьера изображен
на рис.1 (кривая справа). Высота
потенциального барьера
Электроны,
свободно перемещающиеся внутри металла,
не могут выйти за его пределы без затраты
энергии, так как вблизи поверхности
существует потенциальный барьер,
препятствующий
их
вылету.
График потенциального барьера изображен
на рис.1 (кривая справа). Высота
потенциального барьера
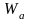 численно равна работе, которую должен
совершить электрон против сил
потенциального барьера. Работу
называют полной работой выхода.
численно равна работе, которую должен
совершить электрон против сил
потенциального барьера. Работу
называют полной работой выхода.
Преодолеть потенциальный барьер и выйти из металла могут лишь те электроны, энергия которых больше . На рис.1 число таких электронов изображается площадью под кривой распределения, расположенной выше уровня (заштрихованная область). Эти электроны, участвующие в эмиссии, называются термоэлектронами.
Поскольку
электроны в веществе даже при Т
= 0 уже обладают энергией Ферми
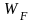 ,
то
для выхода из вещества они должны при
нагревании получить дополнительную
энергию, равную разности уровней энергий
,
то
для выхода из вещества они должны при
нагревании получить дополнительную
энергию, равную разности уровней энергий
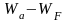 .
Эта разность называется эффективной
работой выхода или просто работой
выхода:
.
Эта разность называется эффективной
работой выхода или просто работой
выхода:
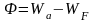 .
.
Работа выхода зависит от типа вещества, его структуры и состояния поверхности.
Количественные расчеты числа эмитированных электронов выполнены на основе квантовой статистики и приведены в литературе [1]. Связь плотности тока эмиссии с температурой определяется формулой РичардсонаДэшмэна:
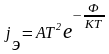 ,
(2)
,
(2)
где
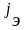 -
плотность термоэлектронного тока.
-
плотность термоэлектронного тока.
Константа A определяется выражением
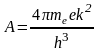 ,
(3)
,
(3)
где и e – масса и заряд электрона;
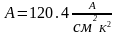 – константа,
одинаковая для всех металлов.
– константа,
одинаковая для всех металлов.
При
экспериментальном исследовании
распределения электронов по скоростям
измеряется ток, т.е. число электронов,
вылетающих с поверхности электрода в
единицу времени. Поэтому для расчета
тока достаточно знать распределение
термоэлектронов по скоростям в одном
направлении
вдоль оси, перпендикулярной поверхности
электрода. Обозначим эту ось Z. Используя
распределение ФермиДирака,
можно получить число электронов в
единице объёма
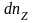 ,
имеющих составляющие скорости вдоль
оси Z в интервале от
,
имеющих составляющие скорости вдоль
оси Z в интервале от
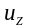 до
до
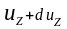 :
:
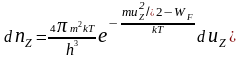 .
(4)
.
(4)
Поток же этих частиц, то есть число электронов, подходящих к единице поверхности в единицу времени будет равен
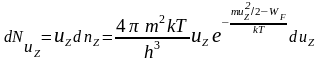 .
(4a)
.
(4a)
Вылетать
из электрода будут только те из электронов,
энергия которых (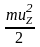 )
больше величины потенциального барьера
(Wa):
)
больше величины потенциального барьера
(Wa):
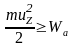 .
.
Скорость
вылетевших электронов
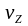 будет меньше скорости
будет меньше скорости
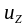 ,
так как часть энергии потратилась на
преодоление потенциального барьера.
При этом кинетическая энергия вылетевших
электронов будет равна
,
так как часть энергии потратилась на
преодоление потенциального барьера.
При этом кинетическая энергия вылетевших
электронов будет равна
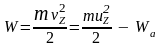 .
(5)
.
(5)
Подставляя (5) в (4а), получим распределение термоэлектронов по скоростям вне электрода:
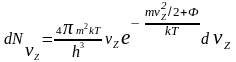
Преобразуем последнее выражение следующим образом:
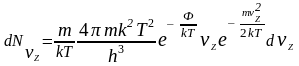 .
(6)
.
(6)
Учитывая выражение (2), получаем
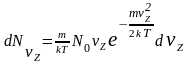 ,
,
где
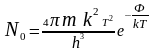
полное число электронов, вылетаюших с
единицы поверхности электрода в единицу
времени.
полное число электронов, вылетаюших с
единицы поверхности электрода в единицу
времени.
Введем
функцию распределения электронов по
скоростям
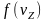 :
:
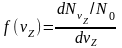 .
(7)
.
(7)
Это
есть дифференциальная
функция
распределения электронов по скоростям.
Физический смысл ее состоит в том, что
величина
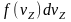 дает ту долю электронов из общего числа
термоэлектронов, которая имеет скорость
в интервале от
дает ту долю электронов из общего числа
термоэлектронов, которая имеет скорость
в интервале от
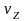 до
до
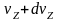 .
.
Используя выражения (7) и (6), получаем дифференциальную функцию распределения по скоростям:
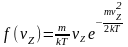 .
(8)
.
(8)
Введем теперь в рассмотрение понятие интегральной функции распределения:
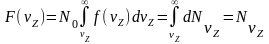 .
(9)
.
(9)
Интегральная
функция распределения показывает
полное число термоэлектронов, обладающих
скоростями, начиная с минимальной
скорости
.
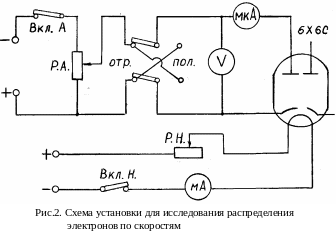 Для
экспериментального изучения законов
распределения термоэлектронов в
настоящей работе используется метод
задерживающего потенциала. Схема
установки приведена на рис. 2.
Для
экспериментального изучения законов
распределения термоэлектронов в
настоящей работе используется метод
задерживающего потенциала. Схема
установки приведена на рис. 2.
Если
на анод вакуумного диода подать
отрицательное напряжение
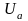 ,
тормозящее движение электронов к аноду,
то попадать на анод будут только те
электроны, энергия которых больше сил
электрического поля по их торможению,
то есть
,
тормозящее движение электронов к аноду,
то попадать на анод будут только те
электроны, энергия которых больше сил
электрического поля по их торможению,
то есть
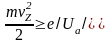 .
(10)
.
(10)
Измеряя анодный ток, мы регистрируем только те электроны, скорость которых выше некоторой скорости , соответствующей условию (10). Таким образом, зависимость анодного тока от величины задерживающего потенциала отражает интегральный закон распределения электронов по скоростям.
Анодный
ток равен
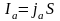 ,
,
где
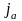
плотность анодного
тока,
S
площадь
поверхности анода.
плотность анодного
тока,
S
площадь
поверхности анода.
Плотность анодного тока определим, используя формулы (8) и (9)
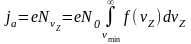 ,
(11)
,
(11)
где
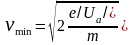 .
.
Интегрируя (11), получаем
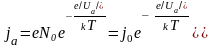 .
.
Отсюда для анодного тока имеем
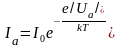 .
(12)
.
(12)
На соотношении (12) основан простой способ проверки закона распределения Максвелла. Логарифмируя (12), получим
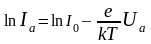 ,
(13)
,
(13)
и,
следовательно, при максвелловском
распределении зависимость
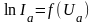 представляет собой прямую, наклон
которой определяется температурой
электронов – температурой катода Т.
представляет собой прямую, наклон
которой определяется температурой
электронов – температурой катода Т.
1. Как связана плотность тока эмиссии с температурой? Назовите основные эмиссионные константы.
2. Каким законам подчиняется ток в диоде при положительном и отрицательном напряжении на аноде?
3. Объяснить, почему и как по вольтамперным характеристикам диода при отрицательном напряжении на аноде можно найти закон распределения термоэлектронов по скоростям.
4. Каков физический смысл интегральной и дифференциальной кривых распределения? Какова связь этих кривых с вероятностными характеристиками?
5. На чем основан метод определения температуры катода?
