14. Ряд Лорана

Определение Функциональный ряд вида: , где – фиксированное комплексное число, – постоянные комплексные числа, k = 0, -1, 1, .. называется рядом Лорана

Область сходимости: представим ряд Лорана в виде:

:

Область сходимости ряда Лорана – общая часть областей сходимости каждого из слагаемых.

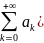– степенной ряд, сходится в круге

Сделаем замену , тогда – степенной ряд относительно , который сходятся в круге к некоторой аналит. функции (

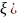
Возвращаясь к z получаем: ( ( - аналитическая функция переменной z вне круг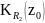а , т.е. на

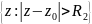
Если , то существует общая область сходимости: круговое кольцо , где ряд сходится к

Если , то ряды не имеют общей области сходимости, ряд Лорана не сходится ни к какой функции

Теорема Лорана Функция f(z) аналитическая в круговом кольце , однозначно разлагается в нем в ряд Лорана, т.е. справедливо . Представление единственное. , где – окружность радиусом p с центром в , ориентирована против ч.с.

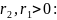
Доказательство. В силу интеграл. Теоремы Коши интегралы, определяющие не зависят от выбора р. Фиксируем произвольную точку . Найдутся два числа и , т.е. . Функция f(z) аналитическая в кольце и непрерывна в =

Напишем интегральную теорему Коши:

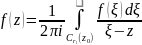- , где и – окружности с направлением обхода против часовой стрелки

Рассмотрим каждое слагаемое. С первым интегралом проделаем тоже самое, что и при доказательстве теоремы о разложении аналитической функции в ряд Тейлора:

; по признаку Вейерштрасса ряд сходится равномерно по , его можно интегрировать почленно] = , где

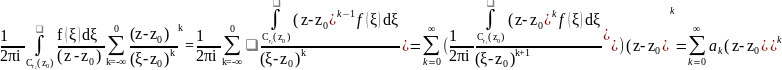Аналогично ; по признаку Вейерштрасса ряд сходится равномерно по , его можно интегрировать почленно] = , где

Учитывая вид коэффициента для двух случаев и независимость интеграла от р, коэффициентам можно придать вид

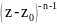Единственность: Пусть существуют два представления , умножим оба ряда на , получим

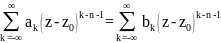
Рассмотрим окружность радиуса . в ней оба ряда сходятся равномерно

Почленно проинтегрируем

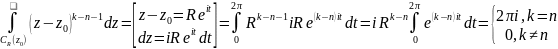
Имеем , придавая числу n различные значения получим , что доказывает единственность разложения функции в кольце

Замечание – ряд Лорана

Первый ряд – главная часть

Второй ряд – правильная или регулярная часть

15 Устранимая особая точка аналитической функции. Поведение аналитической функции в окрестности устранимой особой точки.

Устранимая особая точка z₀ ≠ ∞ является изолированной особой точкой функции f(z). Тогда по теореме Лорана из параграфа 1 функцию f(z) можно разложить в ряд Лорана в кольце (z₀), δ>0:

f(z)=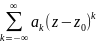 ; ∀z ∈ (z₀) (1)

Определение Изолированная особая точка z₀ называется устранимой, если в разложении (1) все =0 при k<0, то есть разложение (1) имеет вид: f(z)= ; ∀z ∈ (z₀)

Теорема Изолированная особая точка z₀ ≠ ∞ является устранимой особой точкой аналитической функции f(z), тогда и только тогда, когда ∃ δ₁>0, ∃M>0: 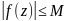; ∀z ∈ (z₀)

То есть функция f(z) ограничена в некоторой проколотой окрестности точки z₀

Доказательство

Необходимость Пусть z₀ устранимая особая точка f(z). Тогда по определению: f(z)= ; ∀z ∈ (z₀)

Доопределим функцию f(z) в точке z₀: f(z₀)=a₀

Имеем: f(z)= ; ∀z ∈ (z₀)

Сумма степенного ряда является аналитической функцией в круге сходимости (z₀), а значит и непрерывной функцией в (z₀)

Поэтому если взять некоторое δ₁>0: 0< δ₁< δ ⇒ f(z) будет непрерывной функцией в замкнутом круге (z₀), а следовательно, т ограниченной в этом круге Ч.т.д.

Достаточность Пусть функция f(z) ограниченна в некоторой проколотой окрестности точки z₀, то есть

∃ δ₁>0, ∃M>0: ; ∀z ∈ (z₀)

Тогда f(z)= ; ∀z ∈ (z₀)

Будем считать что δ₁ было взять так что 0< δ₁< δ. Коэффициенты а_k по теореме Лорана можно представить в виде:

= k=0, ±1, ±2…

Причем а_k не зависит от : 0< < δ₁

Рассмотрим те коэффициенты а_k, для которых k<0. Тогда:

≤ = = M

этом неравенстве к пределу при →0+0. Так как k<0 и коэффициенты не зависят от ρ, то =0 при k<0, и поэтому точка z₀ устранимая особая точка функции f(z)

Ч.т.д.

Следствие Если точка z₀ является устранимой особой точкой функции f(z), то ∃ = ; ∞

Это сразу же следует из равенства:

f(z)= ; ∀z ∈ (z₀)

и непрерывности степенного ряда в точке z₀

Название устранимая особая точка поэтому объясняется тем что если доопределить функцию f(z) в точке z₀: f(z₀)=a₀; то функция f(z) становится аналитической в некоторой окрестности точки z₀, то есть в круге (z₀)