4. Определение конформного отображения в точке и области. Теорема Римана о конформных отображениях (без доказательства). Выяснить будет ли отображение конформным в области

Пусть функция определена в некоторой окрестности точки

Опр. Отображение называется конформным в точке , если оно обладает свойством сохранения углов и постоянством пространства растяжений в точке .

Опр. Отображение называется конформным в области , если функция является однолистной в области и отображение является конформным в каждой точке области

Если функция является аналитической в точке и , то отображение является конформным в точке , причем в некоторой окрестности точки функция однолистна, то есть отображение взаимно-однозначно отображает некоторую окрестность точки в некоторую окрестность точки .

Пусть выполнены следующие условия:

1) Функция является аналитической в области

2) Функция однолистна в области

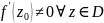
3) Тогда отображение является конформным в области

Справедливо и обратное утверждение. Пусть отображение является конформным в области и область ограничена (Области не содержат бесконечно удаленных точек), тогда функция аналитическая в области , однолистна в области и .

Теорема. Для того что бы отображение , где G ограниченная область (Области не содержат бесконечно удаленных точек), было конформным в области необходимо и достаточно, чтобы функция была аналитической и однолистной в области .

Иногда мы будем рассматривать отображение 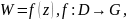где области или одна из них принадлежат рассмотренной комплексной плоскости и содержат бесконечно удаленную точку . Пусть . Рассмотрим три случая.

1) В равенстве сделаем замену . после замены получим отображение

2) В равенстве сделаем замену после замены получим отображение

3) ) В равенстве сделаем замену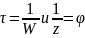 после замены получим отображение

Во всех трех случаях отображения называется конформным в точке , если отображение конформно в точке .

! При таких конформных отображениях уже может не быть аналитической во всех точках . Может существовать одна точка, в окрестности которой не ограничена ( полюс первого порядка)!

Замечание: из аналитичности функции в области и того, что не вытекает, вообще говоря, того, что отображение будет конформным в области , так как функция может оказаться не однолистной в области .

Теорема Римана (без доказательства): Пусть односвязная область расширенной комплексной плоскости, граница которой состоит более чем из одной точки (то есть область отлична от расширенной комплексной плоскости и от расширенной комплексной области с одной выколотой точки). Тогда существует функция такая что отображение конформно отображает область на круг Причем эта функция определяется единственным образом, если выполняется условие: Здесь

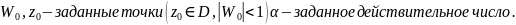
5. Дробно-линейная функция. Круговое свойство.

Функция 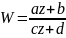называется дробно-линейной, a,b,c,d – заданные комплексные числа. Будем предполагать, что 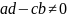, иначе .

1) Случай линейная функция

Пусть Пусть , т. е. точка при таком отображении переходит в точку . Тогда линейная функция осуществляет конформное отображение расширенной комплексной плоскости переменной z на расширенную комплексную плоскость переменной . Ибо, функция однолистна, так как существует обратная функция кроме того отображение комфортно в любой точке 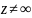. Если , то после замены

получим: или так как A то это отображение конформно в точке так как

2) Случай , тогда функция однолистна в расширенной комплексной плоскости, ибо: точке , для всех остальных точек z расширенной комплексной плоскости обратную функцию можно найти по формуле: . Следовательно, обратная функция однозначна во всех расширенной комплексной плоскости и также является дробно-линейной функцией.

Итак, мы доказали, что дробно-линейная функция однолистна во всей расширенной комплексной плоскости. Докажем теперь, что дробно-линейная функция конформно отображает расширенную комплексную плоскость переменной z на расширенную комплексную плоскость переменной .

1) Случай (доказан выше в это билете)

2) Случай Если то .

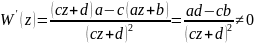Пусть теперь Сделаем замену

Так как следовательно по определению дробно-линейная функция конформна в точке

Наконец пусть Сделаем замену:

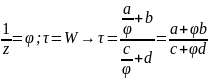
Следовательно, дробно линейная функция конформна в точке . Таким образом, мы полностью доказали, что дробно-линейная функция конформно отображает расширенную комплексную плоскость переменной z на расширенную комплексную плоскость переменной .

Теорема (Круговое свойство). Дробно-линейное отображение переводит любую окружность или прямую на комплексной плоскости переменной z в окружность или прямую на комплексную плоскость переменной ; .

# Пусть , т.е. дробно-линейное отображение является линейным: . Пусть В=0. То есть Но – подобное растяжение плоскости z в раз с центром подобия в центре координат, а равенство означает поворот плоскости вокруг точки z=0 на угол 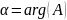. Таким образом линейное отображение есть суперпозиция трех преобразований подобное растяжение плоскости z в раз с центром подобия в точке z=0. 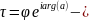поворот плоскости вокруг точки =0 на угол . – параллельный перенос плоскости на вектор . Поэтому линейное преобразование переводит окружности и прямые в прямые. Поэтому в этом случае теорема доказана.

Пусть теперь тогда представим дробно-линейную функцию в виде

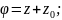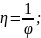Тогда дробно-линейное отображение сводится к последовательному выполнению трех отображений: 1) 2) 3) . Отображения 1)3) линейные, поэтому по доказанному они обладают круговым свойством. Осталось доказать, что отображение 2) или, что то же самое, отображение обладает круговым свойством. Функция конформно отображает расширенную комплексную плоскость переменной z расширенную комплексную плоскость переменной . При этом точка z=0

Уравнение любой окружности или прямой на плоскости 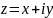имеет вид: При отображении получим: То есть

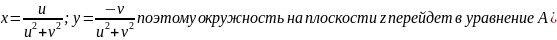это есть уравнение окружности или прямой на плоскости #

Замечание: Можно показать, что дробно-линейное отображение переводит окружности и прямые, проходящие через точку в прямые, а остальные окружности и прямые в окружности.

Замечание: В дальнейшем будем считать, что прямая – это окружность бесконечного радиуса. Поэтому круговое свойство можно короче сформулировать так: при дробно-линейном отображении окружности переходят в окружности.