29. Первая и вторая теоремы разложения. Для рациональной функции

(из рукописных старых лекций) Первая теорема разложения: Если F(p) аналитична в некоторой окр бесконечно удаленной точки и ее разложение в ряд по степеням имеет вид: , то ( и F(p) есть изображения ф-ции f(t)

Док-во

Это выражение получается в результате поточечного перехода к оригиналам в ряде

Те

Сучков:

Рассмотрим простейший случай, когда F(p) рациональная ф-ция, n<m и многочлены не имеют общих нулей. Тогда особые точки F(p) – это полюсы: .

Оригинал существует, тк мы можем разложить дробно-рациональную ф-цию F(p) на простейшие дроби и линейности преобразования Лапласа.

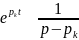Простейшая дробь имеет вид . Тк мы знаем, что при . Тогда по свойству дифференцирования изображения оригинал существует, условие для теоремы выполнено

Пусть - показатель роста F(p) – аналитическая ф-ция при 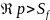и высе особые точки F(p) (полюсы) находятся в левой полуплоскости: . Тогда по формуле Меллина:

О бозначим через – замкнутый контур, состоящий из – полуокружности с центром в точке радиуса R, лежащее левее прямой 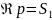и отрезка прямой , где точки – точки пересечения и прямой .

R>0 выбирается столь большим, чтобы все полюсы F(p) (их конченое число) попали внутрь контура . Тогда по основной теореме о вычетах: – полюсы F(p)

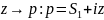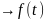Так же . Приравниваем. Перейдем к пределу при . Первый интеграл в левой части по лемме Жордана (В формулировке леммы делаем замену переменной интегрирования ). Второй интеграл по формуле Меллина, а правая часть не зависит от R 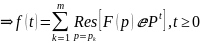– это называется второй теоремой разложения