
- •1. Дифференцируемость функции комплексной переменной. Условия Коши-Римана. Определение аналитической функции в области и точке.
- •2. Аналитичность суммы степенного ряда.
- •3. Геометрический смысл модуля и аргумента производной функции комплексной переменной.
- •4. Определение конформного отображения в точке и области. Теорема Римана о конформных отображениях (без доказательства). Выяснить будет ли отображение конформным в области
- •5. Дробно-линейная функция. Круговое свойство.
- •6. Интегральная теорема Коши для простого и сложного контура.
- •7 .Интегральная формула Коши
- •8.Интеграл типа Коши. Существование производных любого порядка у аналитической функции
- •10.Теорема Морера
- •11.Ряд Тейлора. Единственность разложения в ряд Тейлора.
- •12.Неравенства Коши для коэффициентов степенного ряда. Теорема Лиувилля.
- •13. Теорема единственности аналитической функции. Изолированность ее нулей.
- •14. Ряд Лорана
- •15 Устранимая особая точка аналитической функции. Поведение аналитической функции в окрестности устранимой особой точки.
- •16. Полюс аналитической функции. Поведение аналитической функции в окрестности полюса
- •17. Существенно особая точка аналитической функции. Поведение аналитической функции в окрестности существенно особой точки. Теорема Сохоцкого - Вейерштрасса.
- •18. Вычет аналитической функции относительно конечной и бесконечной изолированной особой точки. Вычисление вычета относительно полюса.
- •19. Основная теорема о вычетах.
- •20. Теорема о сумме вычетов на расширенной комплексной плоскости
- •21. Вычисление несобственных интегралов с помощью вычетов.
- •22. Лемма Жордана
- •23. Вычисление интеграла с помощью леммы Жордана.
- •24. Преобразование Лапласа. Оригиналы и изображения. Показатель роста. Полуплоскость сходимости. Аналитичность изображения ( без док - ва ).
- •25. Линейность преобразования Лапласа. Теоремы подобия, запаздывания и смещения.
- •26. Теоремы о дифференцировании оригиналов и изображений
- •27. Теоремы об интегрировании оригиналов и изображений.
- •29. Первая и вторая теоремы разложения. Для рациональной функции
18. Вычет аналитической функции относительно конечной и бесконечной изолированной особой точки. Вычисление вычета относительно полюса.
Пусть
точка
и функция
аналитическая в некоторой проколотой
окр-ти точки
,
то есть в кольце
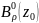 ,
.
Пусть точка
– изолированная особая точка функции
.
Тогда в кольце
функцию
можно разложить в ряд Лорана:
,
.
Пусть точка
– изолированная особая точка функции
.
Тогда в кольце
функцию
можно разложить в ряд Лорана:
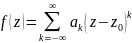 ,
,
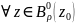 называется число, равное коэффициенту
называется число, равное коэффициенту
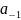 ряда Лорана функции
в некоторой проколотой окрестности
точки
:
,
.
ряда Лорана функции
в некоторой проколотой окрестности
точки
:
,
.
Это
число обозначается символом:
 .
.
Таким
образом,
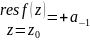
Поскольку
для коэффициента
ряда Лорана была получена формула:
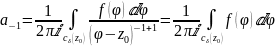 ,
где
,
где
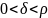 и коэффициент
не
зависит от выбора
,
то для вычета функции
в точке
справедлива формула
и коэффициент
не
зависит от выбора
,
то для вычета функции
в точке
справедлива формула
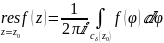 ,
окружность
,
окружность
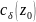 ориентирована против часовой стрелки.
ориентирована против часовой стрелки.
Если
– устранимая особая точка функции
,
то
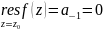 ,
так как в этом случае главная часть ряда
Лорана отсутствует.
,
так как в этом случае главная часть ряда
Лорана отсутствует.
Случай простого полюса (полюса первого порядка)
Пусть
изолированная особая точка
является полюсом первого порядка функции
.
Тогда в некотором кольце
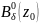 ,
функция
разлагается в ряд Лорана:
,
функция
разлагается в ряд Лорана:
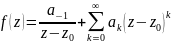 ,
,
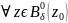 ,
,
,
,
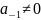 .
Тогда:
.
Тогда:
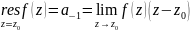 (мы
перешли к пределу при
(мы
перешли к пределу при
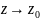 в последнем равенстве и учли, что
в последнем равенстве и учли, что
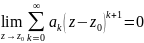 по св-ву степенного ряда.
по св-ву степенного ряда.
Так как точка – полюс первого порядка функции , то ее можно представить в виде:
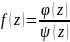 ,
где
,
где
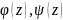 – аналитические в круге
– аналитические в круге
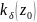 ,
причем
,
причем
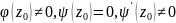 .
.
Тогда
 .
.
То
есть:
 .
.
Случай кратного полюса (полюс порядка
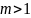 )
)
Пусть изолированная особая точка является полюсом порядка функции . Тогда в некотором кольце , функция разлагается в ряд Лорана:
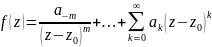 ,
,
,
.
Отметим, что тогда степенной ряд
представляет собой аналитическую
функцию в круге
,
которую можно почленно в этом круге
дифференцировать сколько угодно раз.
Умножим полученное равенство на
,
,
,
.
Отметим, что тогда степенной ряд
представляет собой аналитическую
функцию в круге
,
которую можно почленно в этом круге
дифференцировать сколько угодно раз.
Умножим полученное равенство на
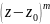 ,
продифференцируем его затем
,
продифференцируем его затем
 раз по переменной
раз по переменной
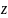 и перейдем к пределу при
.
Тогда:
и перейдем к пределу при
.
Тогда:
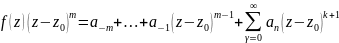 ,
.
,
.
После
дифференцирования
раз и перехода к пределу в правой части
последнего неравенства останется только
член
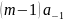 ,
все остальные слагаемые в правой части
либо исчезнут после дифференцирования,
либо обратятся в нуль при переходе к
пределу при
.
Таким образом,
,
все остальные слагаемые в правой части
либо исчезнут после дифференцирования,
либо обратятся в нуль при переходе к
пределу при
.
Таким образом,
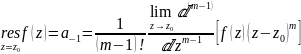
Вычет в бесконечно удаленной точке
Пусть
есть изолированная особая точка
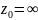 функции
,
то есть существует такое
функции
,
то есть существует такое
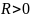 ,
что функция
является однозначной аналитической
функцией в кольце
,
что функция
является однозначной аналитической
функцией в кольце
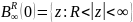 ,
тогда функцию можно разложить в этом
кольце в сходящийся ряд Лорана:
,
тогда функцию можно разложить в этом
кольце в сходящийся ряд Лорана:
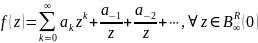
Определение:
Вычетом функции
в точке
называется число, равное
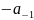 ,
где
– коэффициент ряда Лорана функции
при члене
,
где
– коэффициент ряда Лорана функции
при члене
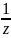 в некоторой окрестности бесконечно
удаленной точки.
в некоторой окрестности бесконечно
удаленной точки.
Это
число обозначается символом
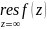 .
.
Таким
образом
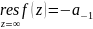 .
Поскольку для коэффициента
ряда Лорана была получена формула:
.
Поскольку для коэффициента
ряда Лорана была получена формула:
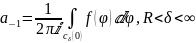 ,
окружность
,
окружность
 ориентирована против часовой стрелки
и коэф-т
не зависит от выбора
,
то для вычета функции
в точке
может и не быть равным нулю, когда эта
точка является устранимой. В этом отличие
вычета функции
в точке
от вычета в конечных точках.
ориентирована против часовой стрелки
и коэф-т
не зависит от выбора
,
то для вычета функции
в точке
может и не быть равным нулю, когда эта
точка является устранимой. В этом отличие
вычета функции
в точке
от вычета в конечных точках.
19. Основная теорема о вычетах.
D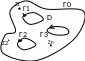 – ограниченная многосвязная область,
граница состоит из замкнутой кусочно-гладкой
кривой Г0
и попарно не пересекающихся кус-гл
кривых Жордана Г1,…,Гm,
расположенных внутри Г0.
– ограниченная многосвязная область,
граница состоит из замкнутой кусочно-гладкой
кривой Г0
и попарно не пересекающихся кус-гл
кривых Жордана Г1,…,Гm,
расположенных внутри Г0.
F(z)
непрерывна в замкнутой области
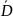 и аналитическая в области D
за искл конечного числа изолированных
особых точек: z1,
z2,
…, zn
и аналитическая в области D
за искл конечного числа изолированных
особых точек: z1,
z2,
…, zn
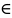 D.
Все кривые ориентированы против часовой
стрелки
D.
Все кривые ориентированы против часовой
стрелки
Тогда
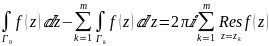 док-во
док-во
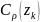
 – окружность
около каждой особой точки k=1,…,n
– окружность
около каждой особой точки k=1,…,n
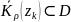 и
и
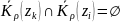 при
при
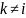 ,
k,i=1,…,n
(окружности попарно не пересекаются).
,
k,i=1,…,n
(окружности попарно не пересекаются).
Рассм
обл D\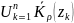 .
Граница области Г. Интегральная теорема
Коши для многосвязной функции – выполнены
условия
.
Граница области Г. Интегральная теорема
Коши для многосвязной функции – выполнены
условия
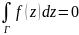
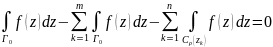
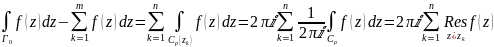
Последнее равенство – опр вычета функции в изолированной особой точке
