Оглавление

1. Дифференцируемость функции комплексной переменной. Условия Коши-Римана. Определение аналитической функции в области и точке. 2

2. Аналитичность суммы степенного ряда. 3

3. Геометрический смысл модуля и аргумента производной функции комплексной переменной. 4

4. Определение конформного отображения в точке и области. Теорема Римана о конформных отображениях (без доказательства). Выяснить будет ли отображение конформным в области 6

5. Дробно-линейная функция. Круговое свойство. 7

6. Интегральная теорема Коши для простого и сложного контура. 9

7.Интегральная формула Коши 11

8.Интеграл типа Коши. Существование производных любого порядка у аналитической функции 12

10.Теорема Морера 14

11.Ряд Тейлора. Единственность разложения в ряд Тейлора. 15

12.Неравенства Коши для коэффициентов степенного ряда. Теорема Лиувилля. 15

13. Теорема единственности аналитической функции. Изолированность ее нулей. 16

14. Ряд Лорана 17

15 Устранимая особая точка аналитической функции. Поведение аналитической функции в окрестности устранимой особой точки. 19

16. Полюс аналитической функции. Поведение аналитической функции в окрестности полюса 20

17. Существенно особая точка аналитической функции. Поведение аналитической функции в окрестности существенно особой точки. Теорема Сохоцкого - Вейерштрасса. 22

18. Вычет аналитической функции относительно конечной и бесконечной изолированной особой точки. Вычисление вычета относительно полюса. 24

19. Основная теорема о вычетах. 26

20. Теорема о сумме вычетов на расширенной комплексной плоскости 26

21. Вычисление несобственных интегралов с помощью вычетов. 26

22. Лемма Жордана 27

23. Вычисление интеграла с помощью леммы Жордана. 28

24. Преобразование Лапласа. Оригиналы и изображения. Показатель роста. Полуплоскость сходимости. Аналитичность изображения ( без док - ва ). 29

25. Линейность преобразования Лапласа. Теоремы подобия, запаздывания и смещения. 30

26. Теоремы о дифференцировании оригиналов и изображений 30

27. Теоремы об интегрировании оригиналов и изображений. 31

29. Первая и вторая теоремы разложения. Для рациональной функции 33

1. Дифференцируемость функции комплексной переменной. Условия Коши-Римана. Определение аналитической функции в области и точке.

Опр. Функция f(z) называется дифференцируемой (моногенной) в точке z₀, если Ǝ конечный предел: 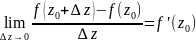. Этот предел называется производной функции f(z) в точке z₀.

Обозначим 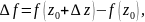тогда из равенства: 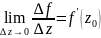следует, что , при Где комплекснозначная функция такая, что

Обратно, если приращение можно представить в виде: при , где А -постоянное комплексное число, не зависящее от 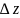, то функция f(z) дифференцируема в точке z₀ и A=f’(z). Следовательно равенство является необходимым и достаточным условием дифференцируемости функции f(z) в точке z₀. В частности, из этого равенства непосредственно следует, что если функция f(z) дифференцируема в точке z₀, то она и непрерывна в этой точке. Функция f(z) называется дифференцируемой в области D, если она дифференцируема в каждой точке этой области.

Из определения производной и свойств пределов вытекают следующие свойства дифференцируемых функций:

1. Пусть функции f(z) и g(z) дифференцируемы в точке z. Тогда их сумма, произведение и частное (при g(z) ) также дифференцируемы в точке z и выполняются равенства:

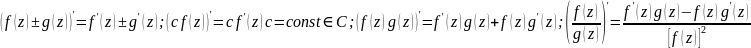
2. Пусть функция W=f(z) дифференцируема в точке z, а функция F(W) дифференцируема в точке W=f(z), тогда сложная функция Ф(z)=F[f(z)] дифференцируема в точке z, причем Ф’(z)=F’(W)f ‘(z).

Теорема (Условие Коши-Римана)

Для того чтобы функция f(z)=u(x,y)+iv(x,y) была дифференцируемой в точке z=x+iy, необходимо и достаточно, чтобы:

1) Функции u(x,y) и v(x,y) были дифференцируемы ы точке (x,y).

2) В точке (x,y) выполнялись условия Коши-Римана:

при этом для f’(x) справедлива формула

# Необходимость. Пусть функция f(z) дифференцируема в точке z. Тогда:

Приравнивая в этом соотношении действительную и мнимую части, имеем: Из этих соотношений и из определения дифференцируемости функции двух вещественных переменных следует дифференцируемость функций . Из этих четырех равенств и обозначения сразу же вытекают формулы (1) и (2).

Достаточность. Пусть функции дифференцируемы в точке и пусть выполняется условие Коши-Римана(1).

Обозначим Тогда из определения дифференцируемости функций и условий (1) получим:

Умножим второе равенство на i и сложим с первым

Или Из определения дифференцируемости функции f(z) в точке z=x+iy следует, что f(z) дифференцируема в точке z=x+iy и . Из последнего равенства и условий (1) вытекает формула (2). #

Опр. 1. Функция f(z) называется аналитической в точке z₀ , если f(z) дифференцируема в некоторой окрестности точки

Опр. 2. Функция f(z) называется аналитической в области D, если f(z) дифференцируема во всех точках области D . Из аналитичности функции f(z) в области D вытекает аналитичность f(z) в каждой точке области D.

2. Аналитичность суммы степенного ряда.

Теорема. Сумма степенного ряда является аналитической функцией в круге сходимости:

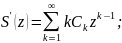# Зафиксируем Обозначим через степенного ряда Согласно сделанному выше замечанию в этом круге определена функция Возьмем 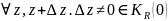и оценим разность

Рассмотрим сначала второе и третье слагаемое в правой части последнего равенства. Так как , то

Зафиксируем это r и оценим сначала вторую сумму:

Так как ряд

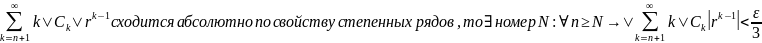
Точно так же оценивается и третья сумма:

Положим теперь n=N и рассмотрим первую сумму при найденном выше N. Вследствие непрерывности суммы конечного числа N непрерывных функций для

Таким образом, мы доказали, что

Следовательно, в точке z существует производная суммы степенного ряда S(z) и она равна S’(z). Так как z – произвольная точка круга сходимости , S(z)в круге сходимости и формула #

Следствие. Степенной ряд в круге сходимости: можно почленно дифференцировать любое число раз, при этом производная суммы исходного ряда равна сумме почленно продифференцированного степенного ряда.

Из доказанно теоремы следует, что функция

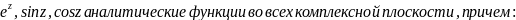
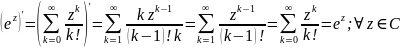
Аналогично доказываются формулы: (cosz)’=-sinz и (sinz)’=cosz 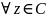Последние две формулы можно доказать и по-другому, используя уже доказанную первую формулу и формулы Эйлера