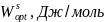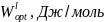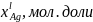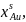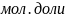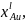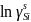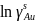МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра МНЭ
отчет
по лабораторной работе № 2
по дисциплине «Физико-химические основы технологии изделий электроники и наноэлектроники»
Тема: Моделирование диаграмм состояния с ограниченной растворимостью компонентов (полупроводник - примесь)»
Студенты гр. 1282 |
____________________ ____________________ ____________________
|
Репкин М.М. Матгафуров Н.И. Козлов С.В. |
Преподаватель |
__________________________ |
Александрова О.А. |
Санкт-Петербург
2023
Лабораторная работа № 2.
Цель работы. Изучение фазовых равновесий в бинарной системе полупроводник (Si, Au) – примесь методом компьютерного моделирования; расчет параметров межатомного взаимодействия; выбор моделей растворов, адекватно описывающих экспериментальные Т-х диаграммы состояния; расчет спинодалей и определение областей устойчивого и метастабильного состояний твердых растворов в заданной системе.
Исходные данные:
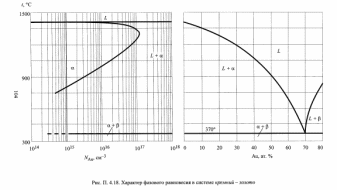
Данные параметры исходных компонентов:
Si:
∆Hпл = 50551 Дж*моль-1
∆Тпл = 1685 К
а = 0,5428 нм
Au:
∆Hпл = 12364 Дж*моль-1
∆Тпл = 1336 К
Тэвт = 643 К Xbэвт = 0.69
Координаты:
Таблица 1 – Координаты точек линии ликвидуса
T, K |
Xbl, мол. доли |
1553 |
0,20 |
1473 |
0,25 |
1323 |
0,36 |
1173 |
0,43 |
1023 |
0,52 |
948 |
0,55 |
873 |
0,60 |
800 |
0,62 |
700 |
0,68 |
643 |
0,7 |
Таблица 2 – Координаты точек линии солидуса
T, K |
Xbs, см-3 |
1690 |
5 |
1690 |
5 10+15 |
1650 |
6 10+16 |
1623 |
8,5 10+16 |
1550 |
2 10+17 |
1473 |
1 10+17 |
1400 |
5 10+16 |
1323 |
2,2 10+16 |
1173 |
4 10+15 |
1023 |
6,5 10+14 |
ОБРАБОТКА РЕЗУЛЬТАТОВ.
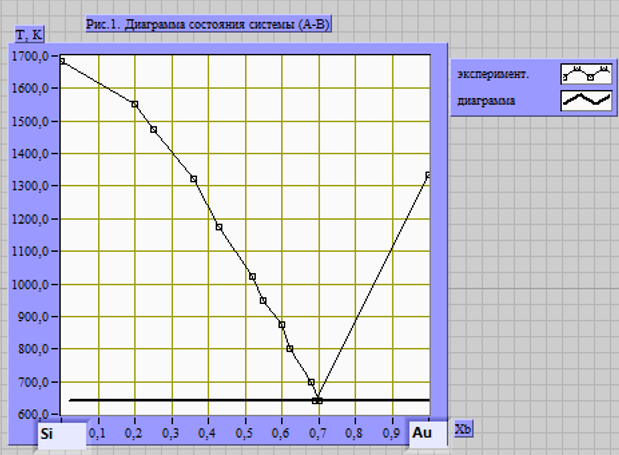
Рисунок
1
 Построенная линия ликвидуса Т-х диаграмма
состояния системы Si-Au
Построенная линия ликвидуса Т-х диаграмма
состояния системы Si-Au
Построение линии ликвидуса на Т-х – проекции диаграммы состояния исследованной системы и нахождение оптимального значения параметров взаимодействия:
Таблица 3 – Оптимальные параметры межатомного взаимодействия
|
|
86000 |
-50741 |
Выбор модели, наиболее адекватно описывающей экспериментальные данные:
Вследствие
малой растворимостью примесей в твердом
германии при анализе линии ликвидуса
можно считать, что в равновесии с жидким
раствором находится кристаллическая
фаза чистого германия, т.е. можно принять
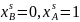 .
.
Расчетная формула:
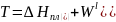
Для
регулярного раствора
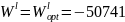 Дж/моль, для квазирегулярного
Дж/моль, для квазирегулярного
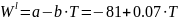 Дж/моль.
Дж/моль.
Для
идеального раствора
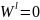 ,
тогда:
,
тогда:
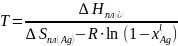
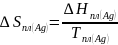
Таблица 4 – Данные для построения линии ликвидуса жидкого раствора
|
Т, К (Идеальный р-р) |
Т, К (Регулярный р-р) |
Т, К (квазирегулярный р-р) |
0,20 |
1586,914 |
1523,1985 |
1586,96 |
0,25 |
1560,638 |
1462,7319 |
1560,71 |
0,36 |
1499,619 |
1304,5375 |
1499,761 |
0,43 |
1457,986 |
1187,3911 |
1458,183 |
0,52 |
1400,309 |
1020,2426 |
1400,586 |
0,55 |
1379,81 |
960,84896 |
1380,116 |
0,60 |
1343,906 |
858,2817 |
1344,26 |
0,62 |
1328,848 |
816,119 |
1329,222 |
0,68 |
1280,768 |
686,31485 |
1281,201 |
0,7 |
1263,598 |
642,10773 |
1264,05 |
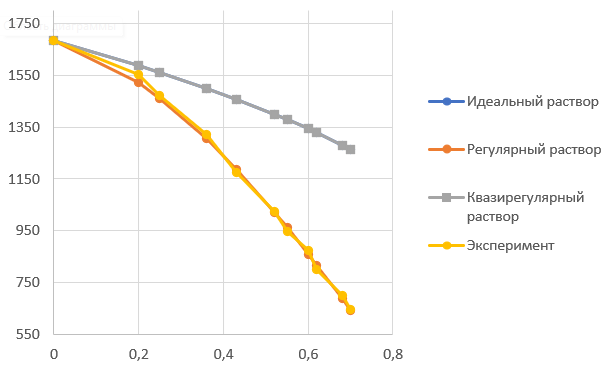
Рисунок 2 – Линии ликвидуса на Т-х проекции диаграммы состояния в рамках моделей идеального, регулярного и квазирегулярного жидкого раствора
Расчёт и построение концентрационных зависимостей коэффициентов активностей компонентов в твёрдом и жидком растворах:
Для твёрдого раствора в пределах области растворимости:
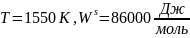
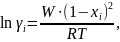
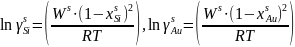
Для жидкого раствора во всём диапазоне составов:
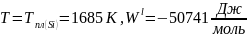
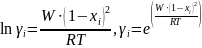
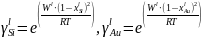
Для
модели идеального раствора:
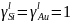
Таблица 5 – коэффициенты активности для растворов
|
Твёрдый раствор |
|
Жидкий раствор |
||||||
|
|
ид. р-р. |
ид. р-р |
|
|
ид. р-р. |
ид. р-р |
||
1∙10-8 |
6,68∙10-16 |
6,676759 |
0 |
0 |
0,0 |
0,03 |
1,00 |
1 |
1 |
1∙10-7 |
6,68∙10-14 |
6,676758 |
0 |
0 |
0,1 |
0,05 |
0,96 |
1 |
1 |
1,2∙10-6 |
9,61∙10-12 |
6,676743 |
0 |
0 |
0,2 |
0,10 |
0,87 |
1 |
1 |
1,7∙10-6 |
1,93∙10-11 |
6,676737 |
0 |
0 |
0,3 |
0,17 |
0,72 |
1 |
1 |
4∙10-6 |
1,07∙10-10 |
6,676706 |
0 |
0 |
0,4 |
0,27 |
0,56 |
1 |
1 |
2∙10-6 |
2,67∙10-11 |
6,676733 |
0 |
0 |
0,5 |
0,40 |
0,40 |
1 |
1 |
1∙10-6 |
6,68∙10-12 |
6,676746 |
0 |
0 |
0,6 |
0,56 |
0,27 |
1 |
1 |
4,4∙10-7 |
1,29∙10-12 |
6,676754 |
0 |
0 |
0,7 |
0,72 |
0,17 |
1 |
1 |
8∙10-8 |
4,27∙10-14 |
6,676758 |
0 |
0 |
0,8 |
0,87 |
0,10 |
1 |
1 |
1,3∙10--8 |
1,12∙10-15 |
6,676759 |
0 |
0 |
0,9 |
0,96 |
0,05 |
1 |
1 |
|
|
|
0 |
0 |
1,0 |
1,00 |
0,03 |
1 |
1 |
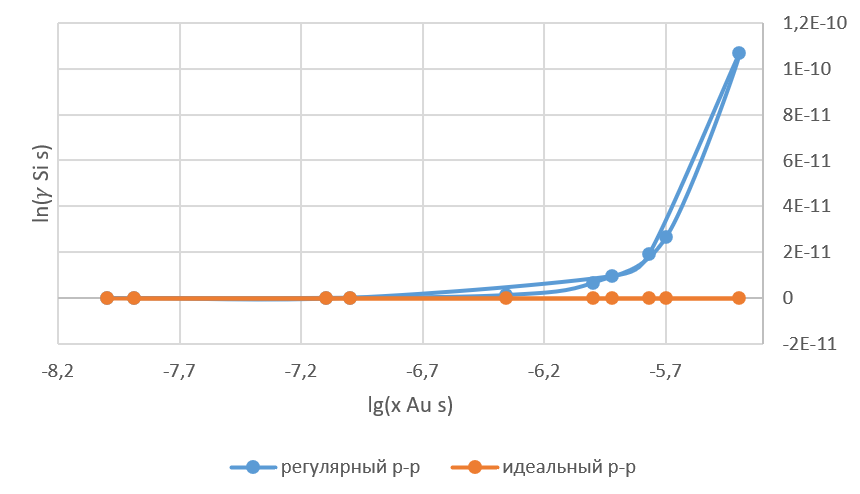
Рисунок 3 – Концентрационная зависимость коэффициента активности Si в твёрдом растворе в пределах области растворимости
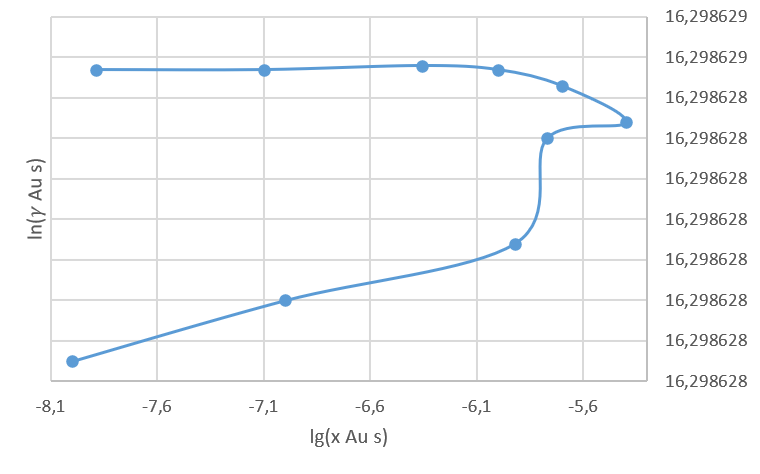
Рисунок 4 – Концентрационная зависимость коэффициента активности Au в твёрдом растворе в пределах области растворимости

Рисунок 5 – Концентрационная зависимость коэффициентов активностей компонентов в жидком растворе во всём диапазоне составов
Расчёт равновесного коэффициента распределения Au по T-x проекции диаграммы состояния системы:
T = 1550 K
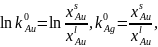
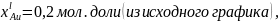
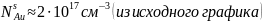
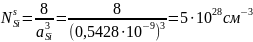
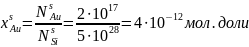
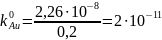
Для модели идеального раствора:
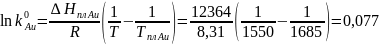 ,
,
откуда
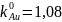
Для модели регулярных растворов:
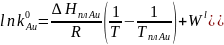
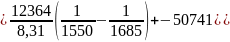
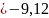 ,
откуда
,
откуда
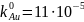
Для модели квазирегулярного раствора:
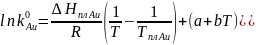
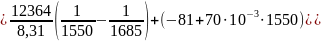
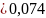 ,
откуда
,
откуда
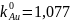
Расчёт и построение спинодали при температурах от
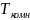 до
до
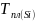 :
:
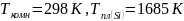
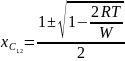
Таблица 6 граничные составы (спинодали)
T, К |
С1 |
С2 |
298 |
0,985 |
0,015 |
412 |
0,980 |
0,020 |
526 |
0,974 |
0,026 |
640 |
0,968 |
0,032 |
754 |
0,962 |
0,038 |
868 |
0,956 |
0,044 |
982 |
0,950 |
0,050 |
1096 |
0,944 |
0,056 |
1210 |
0,938 |
0,062 |
1324 |
0,931 |
0,069 |
1438 |
0,925 |
0,075 |
1552 |
0,918 |
0,082 |
1685 |
0,911 |
0,089 |
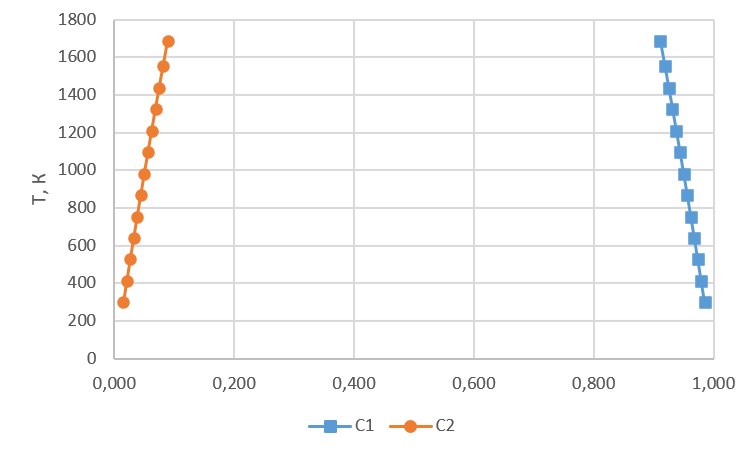
Рисунок 6 – Зависимость граничных составов от температуры (спинодали)
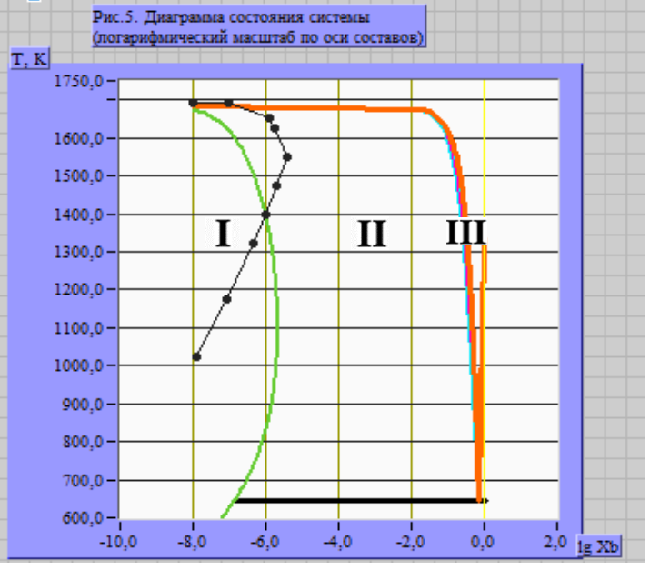
![]()
Рисунок 7 – Крупномасштабная T-x-проекция диаграмма системы
ВЫВОД
В
этой лабораторной работе было изучено
фазовое равновесие в бинарной системе
полупроводник (Si)
– примесь (Au)
с помощью компьютерного моделирования.
Найдены оптимальные параметры межатомного
взаимодействия
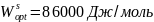 и
и
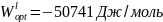 .
Был проведен расчет спинодалей и
определение областей устойчивого и
метастабильного состояний твердых
растворов в заданной системе.
.
Был проведен расчет спинодалей и
определение областей устойчивого и
метастабильного состояний твердых
растворов в заданной системе.

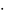 10+14
10+14