
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В. И. Ульянова (Ленина)
Кафедра микро- и наноэлектроники
отчет
по лабораторной работе №1
по дисциплине «Физико-химические основы технологии изделий электроники и наноэлектроники»
Тема: Моделирование диаграмм состояния полупроводниковых систем с неограниченной растворимостью компонентов в жидкой и твёрдой фазах
Студент гр. 1282 |
|
.В. |
Преподаватель |
|
Александрова О.А |
Санкт-Петербург
2023
ЦЕЛЬ РАБОТЫ
Цель
работы заключается в проведении
компьютерного моделирования фазовых
равновесий в бинарных полупроводниковых
системах с непрерывным твердым раствором.
Это включает в себя расчет параметров
взаимодействия между атомами, выбор
подходящих моделей растворов, которые
наилучшим образом описывают
экспериментальные
 проекции диаграмм состояния.
проекции диаграмм состояния.
ИСХОДНЫЕ ДАННЫЕ

Рисунок
1
 T-x
проекция диаграммы состояния системы
GaSb
AlSb
T-x
проекция диаграммы состояния системы
GaSb
AlSb
Таблица 1 – Справочные данные по фазовым переходам
|
|
|
|
65,1 |
985 |
|
82,0 |
1333 |
ОБРАБОТКА РЕЗУЛЬТАТОВ
Построим проекции
 диаграмм состояния (экспериментальной
и теоретической), а также найдем
оптимальные значения параметров
взаимодействия
диаграмм состояния (экспериментальной
и теоретической), а также найдем
оптимальные значения параметров
взаимодействия
 .
На рисунке 2 отображены данные, по
которым будет производиться построение,
изображенное на рисунке 3.
.
На рисунке 2 отображены данные, по
которым будет производиться построение,
изображенное на рисунке 3.

Рисунок
2
 Координаты точек ликвидуса и солидуса
Координаты точек ликвидуса и солидуса

Рисунок 3 T-x проекция диаграммы состояния (экспериментальная и теоретическая)
Оптимальные параметры межатомного взаимодействия:
Таблица 2 – Значения параметров взаимодействия
|
|
|
|
Сопоставляя диаграммы состояния, полученные экспериментально и теоретически, можно заметить, что различия между экспериментальными и теоретическими кривыми незначительны. Расхождения могут быть объяснены погрешностью в выборе значений мольных долей компонента B.
Проведем построение проекции T-x диаграмм состояния в соответствие с пунктом №11 методических указаний.

Рисунок
4
T-x
проекция диаграммы состояния c
учетом влияния знака и абсолютного
значения параметров
 на положение линий ликвидуса и солидуса
на положение линий ликвидуса и солидуса
Пояснение:
изменение знака и абсолютного значения
параметров
приводит к смещению положения кривых.
Увеличение значения
 к опусканию кривой солидуса, а увеличение
значения
к опусканию кривой солидуса, а увеличение
значения
 —
к поднятию кривой ликвидуса. Параметры
взаимодействия представляют собой
энергетические характеристики и являются
индикатором отклонения раствора от
идеального состояния.
—
к поднятию кривой ликвидуса. Параметры
взаимодействия представляют собой
энергетические характеристики и являются
индикатором отклонения раствора от
идеального состояния.
Рассчитаем и построим концентрационные зависимости термодинамических функций смешения
 для твердого и жидкого растворов.
Приведем пример расчета, полученные
результаты сведем в таблицы №3 и №4. На
рисунках 4 и 5 изобразим зависимости
функций смешения для жидкого и твердого
растворов соответственно.
для твердого и жидкого растворов.
Приведем пример расчета, полученные
результаты сведем в таблицы №3 и №4. На
рисунках 4 и 5 изобразим зависимости
функций смешения для жидкого и твердого
растворов соответственно.
Пример
оценки параметров для жидкого раствора
( :
:


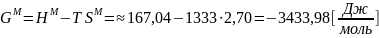
Таблица 3 – Значения термодинамических функций смешения для жидкого раствора
|
∆ |
∆ |
∆ |
0 |
0 |
0 |
0 |
0,1 |
2,70 |
167,04 |
-3433,98 |
0,2 |
4,16 |
296,96 |
-5246,11 |
0,3 |
5,08 |
389,76 |
-6376,92 |
0,4 |
5,59 |
445,44 |
-7009,67 |
0,5 |
5,76 |
464 |
-7214,15 |
0,6 |
5,59 |
445,44 |
-7009,67 |
0,7 |
5,08 |
389,76 |
-6376,92 |
0,8 |
4,16 |
296,96 |
-5246,11 |
0,9 |
2,70 |
167,04 |
-3433,98 |
1 |
0 |
0 |
0 |

Рисунок 5 – Концентрационные зависимости термодинамических функций для жидкого раствора
Пример
оценки параметров для твердого раствора
( :
:


Таблица 4 – Значения термодинамических функций смешения для твердого раствора
, мол. дол. |
∆ , Дж/(моль*К) |
∆ , Дж/моль |
∆ , Дж/моль |
0 |
0 |
0 |
0 |
0,1 |
2,70 |
115,02 |
-2545,90 |
0,2 |
4,16 |
204,48 |
-3891,49 |
0,3 |
5,08 |
268,38 |
-4731,76 |
0,4 |
5,59 |
306,72 |
-5202,12 |
0,5 |
5,76 |
319,5 |
-5354,15 |
0,6 |
5,59 |
306,72 |
-5202,12 |
0,7 |
5,08 |
268,38 |
-4731,76 |
Продолжение Таблицы 4
0,8 |
4,16 |
204,48 |
-3891,49 |
0,9 |
2,70 |
115,02 |
-2545,90 |
1 |
0 |
0 |
0 |

Рисунок 6 – Концентрационные зависимости термодинамических функций для твердого раствора
Рассчитаем и построим концентрационные зависимости коэффициентов активностей и активностей компонентов в твердом и жидком растворах при
 .
Полученные значения сведем в таблицу
№5 для компонента (А) и таблицу №6 для
компонента (В).
.
Полученные значения сведем в таблицу
№5 для компонента (А) и таблицу №6 для
компонента (В).
Пример
оценки параметров для регулярного
раствора в твердом состоянии
для компонента (А) :
:


Таблица 5 – Значения активностей и коэффициентов активности для компонента (А)
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
0,1 |
0,901 |
1,002 |
0,902 |
1,002 |
0,2 |
0,805 |
1,006 |
0,805 |
1,007 |
0,3 |
0,710 |
1,014 |
0,711 |
1,015 |
0,4 |
0,615 |
1,025 |
0,616 |
1,027 |
0,5 |
0,520 |
1,040 |
0,521 |
1,043 |
0,6 |
0,423 |
1,058 |
0,425 |
1,062 |
0,7 |
0,324 |
1,080 |
0,326 |
1,086 |
0,8 |
0,221 |
1,105 |
0,223 |
1,113 |
0,9 |
0,113 |
1,135 |
0,115 |
1,145 |
1 |
0 |
1,169 |
0 |
1,182 |
Таблица 6 – Значения активностей и коэффициентов активности для компонента (B)
|
|
|
|
|
0 |
0 |
1,169 |
0 |
1,182 |
0,1 |
0,113 |
1,135 |
0,115 |
1,145 |
0,2 |
0,221 |
1,105 |
0,223 |
1,113 |
0,3 |
0,324 |
1,080 |
0,326 |
1,086 |
0,4 |
0,423 |
1,058 |
0,425 |
1,062 |
0,5 |
0,520 |
1,040 |
0,521 |
1,043 |
0,6 |
0,615 |
1,025 |
0,616 |
1,027 |
0,7 |
0,710 |
1,014 |
0,711 |
1,015 |
0,8 |
0,805 |
1,006 |
0,805 |
1,007 |
0,9 |
0,901 |
1,002 |
0,902 |
1,002 |
1 |
1 |
1 |
1 |
1 |
Для идеального раствора выполняются
условия:
 ;
; ;
;
 .
.
По данным таблица №5 и №6 построим концентрационные зависимости.

Рисунок 7 – Концентрационная зависимость активности компонентов в жидкой фазе в сравнении с идеальным раствором

Рисунок 8 – Концентрационная зависимость активностей компонентов твёрдого раствора в сравнение с идеальным раствором

Рисунок 9 – Концентрационная зависимость логарифма коэффициента активности в твердой фазе

Рисунок 10 – Концентрационная зависимость логарифма коэффициента активности в жидкой фазе
Рассчитаем и построим температурную зависимость коэффициента активности компонентов А и В в твердом растворе для одного состава
 [мол.дол].
[мол.дол].
Пусть температура будет принимать
значения .
.
Оценим
 для температуры
для температуры
 :
:


Таблица 7 – Значения коэффициентов активности в твердом растворе при
T, К |
|
|
|
1000 |
1 |
0,038 |
0,038 |
1010 |
1,01 |
0,038 |
0,038 |
1050 |
1,05 |
0,037 |
0,037 |
1100 |
1,1 |
0,035 |
0,035 |
1173 |
1,173 |
0,033 |
0,033 |
1206 |
1,206 |
0,032 |
0,032 |
1239 |
1,239 |
0,031 |
0,031 |
1250 |
1,25 |
0,031 |
0,031 |
1280 |
1,28 |
0,030 |
0,030 |
1300 |
1,3 |
0,030 |
0,030 |

Рисунок 11 – Температурная зависимость коэффициента активности компонента А

Рисунок 12 – Температурная зависимость коэффициента активности компонента B
Воспользуемся проекцией диаграммы состояния для расчета равновесных коэффициентов распределения компонентов А и В при заданной температуре

Рассчитаем рабочую температуру

Пусть
 ,
тогда
,
тогда
 ,
,

Произведем оценку равновесного коэффициента распределения несколькими способами:
Оценка исходя из определения равновесного коэффициента распределения
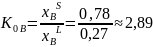

Оценка по модели идеального раствора ( ; .)

Откуда
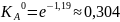

Откуда

Оценка по модели регулярного раствора


Откуда



Откуда


Рисунок
12
–
Определение
мольных долей компонентов при
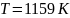
ВЫВОД
В ходе работы были изучены фазовые равновесия в бинарных полупроводниковых системах с непрерывным твердым раствором, пользуясь метод компьютерного моделирования.
Был
произведен расчет параметров межатомного
взаимодействия, оптимальными значениями
являются
 и
и
 .
.
Также были построены концентрационные зависимости термодинамических функций смешения, активностей и активностей компонентов в твердом и жидком растворах.
При
определение равновесного коэффициента
распределения компонентов была посчитана
рабочая температура
 при которой проводились все расчеты.
при которой проводились все расчеты.










 ,
мол. дол.
,
мол. дол. ,
Дж/(моль
,
Дж/(моль К)
К) ,
Дж/моль
,
Дж/моль ,
Дж/моль
,
Дж/моль



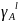
 /,
/,

