2.2 Расчет параметров реакции при необходимых условиях

Для расчета термодинамических параметров при температурах отличных от стандартной, необходимо воспользоваться законом Кирхгофа для одной фазы. Для изменения энтальпии (6) и для изменения энтропии (7)

Результаты расчета представлены в таблице 3.

(6)

(7)

Пример расчета для температуры 388 K

Далее по уравнению Гиббса-Гельмгольца для температуры 388 K

Логарифм константы равновесия при заданной температуре

Таблица 3 – Расчетные значения термодинамических величин

	, К-1					lg Kp
298	3.356	-475.970	-205.600	-414.701	167.461	72.727
388	2.577	-476.315	-206.632	-396.143	122.862	53.358
505	1.980	-476.425	-206.892	-371.945	88.631	38.492
900	1.111	-473.965	-203.600	-290725	38.872	16.882

2.3 Выбор рабочей точки и анализ условий протекания процесса

На рисунке 3 представлен график зависимости логарифма константы равновесия от f (1/Т). Так же на графике обозначены области возможности и невозможности протекания реакции.

Рабочий диапазон температур равен 0.7…0.9 Т_{пл (SnS)}, то есть от 807.1 К до 1037.7 К. Рабочая температура, выбранная из полученного диапазона равна 900 К. Термодинамические параметры при заданной температуре представлены в таблице 3.

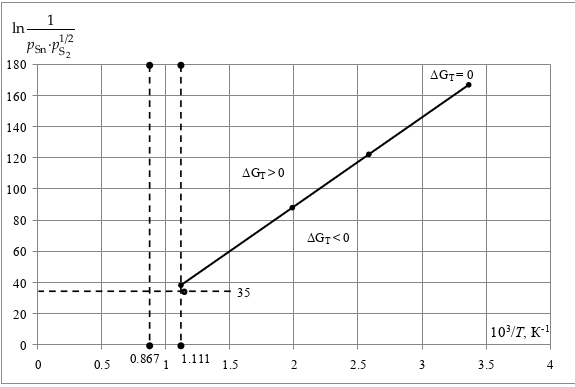
Рисунок 3 – Анализ возможности протекания процесса и выбор рабочей точки

При данной температуре значение логарифма константы равновесия – 38.872. Рабочая точка выбирается при этой же температуре, но с меньшим значением логарифма константы равновесия, для того что бы перейти в область самопроизвольного протекания процесса в прямом направлении (ΔG_T < 0).

Условия, обеспечивающие протекание реакции исследуются с помощью уравнения изотермы химической реакции

(8)

Тогда условие равновесия в системе при 900K ( )

Условие протекания в прямом направлении при 900K ( )

Невозможность протекания в прямом направлении при 900K ( )

Тогда значение логарифма произведения реальных давлений паров принимается 35 < 38.872.

3. Анализ процессов сублимации

1. Анализ сублимации и испарения олова Sn

Уравнение реакции для процесса сублимации олова

Константа равновесия в данном случае будет только от парциального давления газообразного олова

Параметры реакции при температуре 298 К определяются по формулам (1)…(5)

В данном процессе необходимо учесть фазовый переход, поэтому рассчитываются теплоемкости при Т < Т_фп и при Т > Т_фп

• (Т < Т_фп)

• (Т > Т_фп)

При температурах выше Т_пл изменение энтальпии (6) и изменение энтропии (7) находятся также по закону Кирхгофа, но в данном случае с учетом фазовых переходов. Результаты представлены в таблице 4.

Пример расчета для температуры 900 K

Далее по уравнению Гиббса-Гельмгольца для температуры 900 K

Логарифм константы равновесия при заданной температуре

Таблица 4 – Расчетные значения термодинамических величин для процесса сублимации олова

	, К-1					lg Kp	lg PSn
298	3.356	301.500	117.300	266.545	-107.634	-46.745	-46.745
388	2.857	301.902	118.487	255.929	-79.376	-34.472	-34.472
505	1.548	302.229	119.236	242.014	-57.670	-25.046	-25.046
900	1.111	297.799	109.060	199.645	-26.690	-11.591	-11.591

Зависимость ln P_Sn от обратной температуры для олова представлена на рисунке 4.

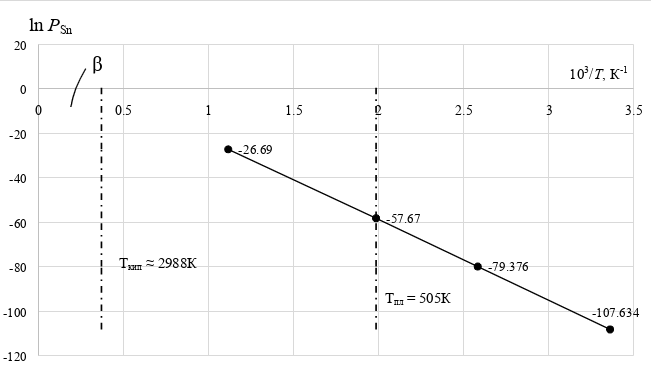
y = -35.631x + 11.918

Рисунок 4 – Зависимость ln P_Sn от обратной температуры

Представив логарифм давления пара олова в виде полинома

Получается уравнение аппроксимирующей прямой

Температура кипения находится из условия, что давления пара олова сравнивается с атмосферным и ln P_Sn = 0

Температура кипения