полезные файлы (наверное) / Metody_matematicheskoy_fizki_Merkulov

+1 +1

XX

L(v) = ckL(yk) = ck kyk;

k=1 k=1

получаем

XX

ck kyk(x) = gkyk(x):

+1

X

v(x) = ck cos( k(3 x))

k=1

и решение исходной задачи

+1

X

u(x) = ck cos( k(3 x)) + x 4:

k=1

В качестве приближенного решения задачи можно взять частичную сумму ряда Фурье

N

X

uN (x) = ck cos( k(3 x)) + x 4:

k=1

В табл. 1.1 приведены значения приближенного решения u3(x). Для сравнения приводятся значения точного решения

20

Получить точное решение исходной задачи читателю предлагается самостоятельно.

1.5. Уравнение Бесселя. Функция Бесселя

Уравнением Бесселя порядка p (где p 0 – заданное число) называется следующее дифференциальное уравнение:

Уравнение (1.19) – линейное однородное дифференциальное уравнение второго порядка. Его общее решение состоит из двух линейно независимых функций. Будем искать решение уравнения (1.19) в виде обобщенного степенного ряда

k=0

Здесь a0 – первый ненулевой коэффициент ряда. Почленно дифференцируя ряд (1.20), найдем y0. Затем, умножив на x и снова продифференцировав, получим

x(xy0)0 = a0 2x + a1( + 1)2x +1 + a2( + 2)2x +2 + :::

+ ak( + k)2x +k + ::: :

Подставив выражения для x(xy0)0 и для y в уравнение (1.19), получим a0 2x + a1( + 1)2x +1 + a2( + 2)2x +2 + ::: + ak( + k)2x +k + :::

+a0x +2 + ::: + ak 2x +k + :::

p2a0x p2a1x +1 p2a2x +2 ::: p2akx +k ::: = 0:

Приравняв нулю сумму коэффициентов при каждой степени x, составим бесконечную систему уравнений для определения коэффициентов

8

>a0( 2 p2) = 0;

>

>

>

>a1[( + 1)2 p2] = 0;

>

>

>

>a [( + 2)2 p2] + a = 0;

> 2 0

<

>

>

>

>

>

>

>

>

:. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

21

Из первого уравнения получаем 2 p2 = 0 (так как a0 6= 0), следовательно,= p. Пусть = p. Перепишем систему, преобразовав выражения в квадратных скобках:

8

>>a1(2p + 1) = 0;

>

>

>a 2(2p + 2) + a = 0;

> 2 0

>

>

<a33(2p + 3) + a1 = 0;

>. . . . . . . . . . . . . . . . . . . . . . . .

>

>

>

>akk(2p + k) + ak 2 = 0;

>

>

>

:. . . . . . . . . . . . . . . . . . . . . . . .

Отсюда видно,что a1 = 0 и все коэффициенты с нечетными номерами равны 0. Коэффициенты ak с четными номерами будут выражаться через a0. Поскольку решение линейного уравнения определяется с точностью до постоянного множителя, значение a0 можно положить произвольным. Пусть

1

a0 = 2p (p + 1), где (p + 1) – гамма-функция. Тогда

При выводе этих соотношений использовано основное свойство гамма-фун- кции z (z) = (z+1). Все коэффициенты ряда найдены, и можно записать решение уравнения (1.19) в виде

Полученный ряд абсолютно сходится для всех значений x (это легко проверить с помощью признака Даламбера). Сумма этого ряда называется функцией Бесселя порядка p и обозначается Jp(x):

Если в первом уравнении системы (1.21) положить = p, то аналогичными рассуждениями можно получить представление в виде ряда

22

функции Бесселя отрицательного порядка. В случае, когда p – не целое число, это представление имеет вид

Функции Jp(x) и J p(x) линейно независимы, и, следовательно, общее решение уравнения Бесселя

y(x) = C1Jp(x) + C2J p(x):

В случае, когда p = m – целое число, оказывается, что первые n коэффициентов ряда (1.23) равны нулю и функция Бесселя с целым отрицательным индексом

т. е. функции Jm(x) и J m(x) оказались линейно зависимы и, следовательно, не образуют фундаментальную систему решений уравнения (1.19). Можно доказать, что линейно независимую пару решений составляют функции Jp(x) и Np(x), где функция Np(x), называемая функцией Неймана, определяется как

Np(x) = cos(p )Jp(x) J p(x) sin(p )

для нецелых значений p и

Nm(x) = lim cos(p )Jp(x) J p(x)

p!m

для целого индекса.

Из формулы (1.23) видно, что первое слагаемое ряда для функции

ниченна. Также неограниченны при x ! 0 функции Np(x) и Nm(x), поэтому ограниченное в нуле решение уравнения Бесселя имеет вид

y(x) = CJp(x):

23

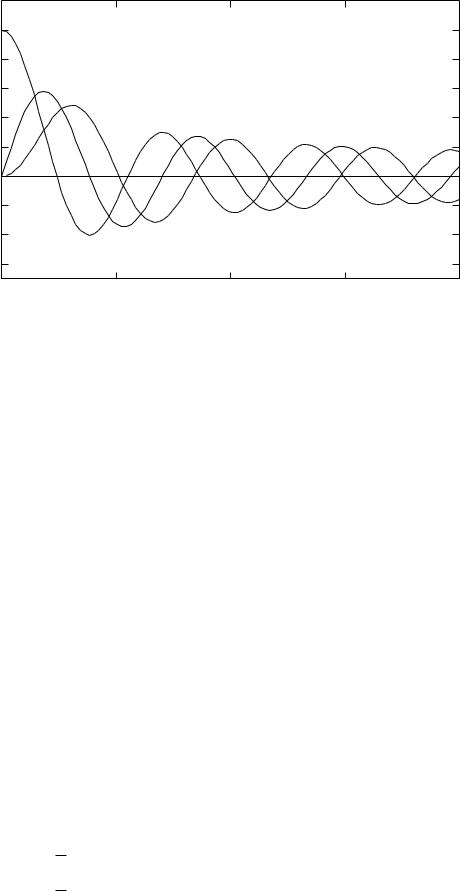
На рис. 1.2 приведены графики функции J0(x), J1(x) и J2(x) [5]. Справедливо [6] следующее асимптотическое представление:

Отсюда следует, что при больших x график Jp(x) имеет колебательный характер с амплитудой, стремящейся к нулю.

Обозначим через k, k, k соответственно положительные корни уравнений

Jp(x) = 0; Jp0(x) = 0; xJp0(x) + SJp(x) = 0 (S > 0):

Справедливы следующие утверждения [6]:

2)k, k, k – простые корни;

3)k < k < k:

Используя представление функций Бесселя в виде ряда (1.22), можно получить следующие тождества, связывающие функции Бесселя с разными индексами и их производные:

1)(xpJp(x))0 = xpJp 1(x);

2)(x pJp(x))0 = x pJp+1(x);

3)Jp 1(x) = xp Jp(x) + Jp0(x);

4)Jp+1(x) = xp Jp(x) Jp0(x);

24

n=0

Доказательство остальных тождеств рекомендуем читателю в качестве самостоятельного упражнения.

1.6.Задача на собственные значения для оператора Бесселя

Оператором Бесселя называется дифференциальный оператор вида

Bp(y) = 1(xy0)0 + p2 y: x x2

В качестве области определения оператора D(B) возьмем множество дважды дифференцируемых функций, заданных на промежутке [0; T ] и удовлетворяющих однородным краевым условиям:

y(x) ограничена при x ! 0 + 0; Ry0(T ) + Sy(T ) = 0;

где R, S – некоторые постоянные, R 0, S 0, jRj + jSj =6 0. Рассмотрим для оператора Bp(y) задачу на собственные значения

>

>

>

>

:p 0; R; S 0 (p = 0; S > 0):

25

Можно показать, что собственные числа этой задачи положительны. Перепишем уравнение задачи (1.24) в виде

p

и сделаем замену переменной t = x. Тогда справедлива цепочка ра-

Полученное уравнение – это уравнение Бесселя. Его ограниченным

Как известно из 1.5, это уравнение имеет множество простых корнейk, k = 1; 2; ::: . В случае, если R = 0 или S = 0, уравнение (1.27) превраща-

ется в Jp( ) = 0 или Jp0( ) = 0 с аналогичными свойствами. Следовательно, p

будет собственным числом задачи, если T = k. Таким образом, получено множество собственных чисел

k = k 2 ;

T

где k – корень уравнения (1.27), k = 1; 2; :::; и множество собственных функций

Для того чтобы разложить функцию в ряд по системе ортогональных функций Бесселя, потребуется несколько интегральных тождеств.

26

Утверждение 1.5. Для любых ; 2 R, 6= , выполняется

27

= Jp0( )Jp( ) Jp0( )Jp( ):

Поделив на 2 2 , получим формулу (1.28).

T 2

Утверждение 1.6. Для любого 6= 0 справедлива формула

Доказательство. В выражении (1.28) сделаем предельный переход при ! и применим правило Лопиталя: