лаба6 / Metrologia_6
.docx
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИИСТ
отчет
по лабораторной работе №6
по дисциплине «Метрология»
Тема: «ДИНАМИЧЕСКИЙ РЕЖИМ СРЕДСТВ ИЗМЕРЕНИЙ»
Студент гр. 1282 |
|
КАТ |
Преподаватель |
|
Минаев А.В. |
Санкт-Петербург
2022
Лабораторная работа №4
«Электронно-лучевой осциллограф»
Цель: изучение динамического режима средств измерений.
Задание.
Ознакомиться с лабораторной установкой. Собрать схему исследования
динамического звена 2-го порядка. Получить у преподавателя задание на
выполнение
лабораторной работы. Записать частоту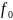
собственных колебаний и коэффициент
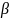демпфирования (степень успокоения) для
заданных вариантов реализации
динамического звена.
Исследовать динамический режим заданных средств измерений при ступенчатом изменении входного сигнала.
Определить динамическую погрешность при заданных параметрах звена 2-го порядка и выбранных амплитуде и частоте входных сигналов прямоугольных импульсов; погрешность определить в 6…10 точках на одном полупериоде входного сигнала. Построить графики входного и выходного сигналов исследуемого средства. Построить графики динамической погрешности. По результатам исследований сделать выводы о влиянии f0 и/или на характер изменения выходного сигнала и динамическую погрешность.
Определить время
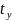установления выходного сигнала для
различных частот f0i собственных
колебаний при заданном коэффициенте
демпфирования .
Построить график зависимости tу = F(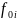
)
при
= const. При определении времени установления
принять погрешность асимптотического
приближения переходного процесса,
равную 5 % от установившегося значения.
Определить время tу установления выходного сигнала для различных коэффициентов i демпфирования при заданной частоте f0 собственных колебаний. Построить график зависимости tу = F(i) при f0 = const. По результатам пунктов 2.2, 2.3 сделать выводы о влиянии f0 и на время установления tу.
Исследовать динамический режим средств измерений при синусоидальном входном воздействии. Определить погрешности в динамическом режиме при указанных параметрах (f0, ) звена 2-го порядка и заданной частоте входного сигнала; погрешности определить в 8…10 точках на одном периоде сигнала. Построить графики входного и выходного сигналов, график динамической погрешности. Сделать вывод о характере изменения динамической погрешности и оценить ее максимальное (амплитудное) значение.
Общие сведения:
Идеальные в
динамическом смысле средства измерений
СИи, иначе безынерционные, имеют, как
правило, линейную зависимость выходного
сигнала
(t)
от входного x(t):
(t)
=
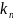x(t),
где
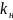– номинальный коэффициент преобразования.
Очевидно, что в таких средствах измерений
выходной сигнал во времени полностью
повторяет входной с точностью до
множителя
.
В реальных средствах измерений СИр выходной сигнал y(t) в силу указанных причин будет иметь более сложную зависимость от входного сигнала, в частности, описываемую дифференциальными уравнениями соответствующего порядка.
Разность между выходным сигналом y(t) реального средства измерений и выходным сигналом (t) (сигнал идеального средства измерений) при одном и том же входном сигнале x(t) определяет динамическую погрешность по выходу реального средства СИр измерений:
y(t) = y(t) – (t) (6.1)
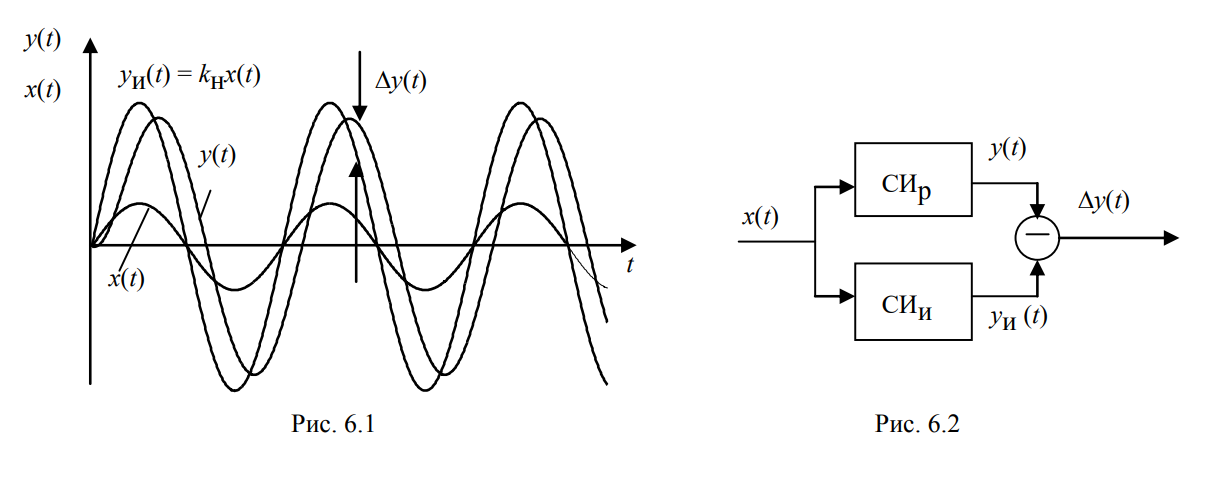
Рисунок 6.1 иллюстрирует возможный вариант входного x(t) и выходных (t) , y(t) сигналов идеального и реального средств измерений и возникающую при этом динамическую погрешность y(t). На рис. 6.2 показана структурная схема, удобная для интерпретации и оценки возникающей динамической погрешности.
Обработка результатов:
1. Рассчитаем значение динамической погрешности в каждом случае:
1)
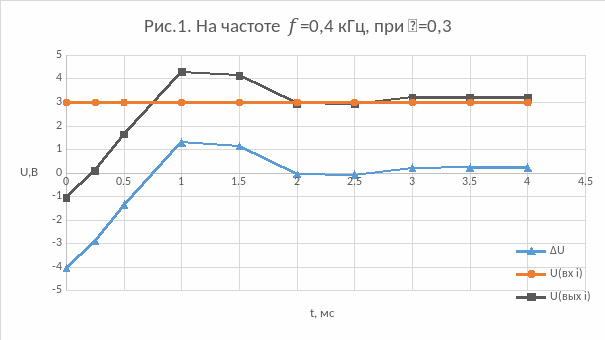
На частоте:
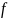=0,4
кГц, при =0,3:
|
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
-1,05 |
0,1 |
1,64 |
4,29 |
4,13 |
2,94 |
2,92 |
3,21 |
3,22 |
3,22 |
ΔU,В |
-4,05 |
-2,9 |
-1,36 |
1,29 |
1,13 |
-0,06 |
-0,08 |
0,21 |
0,22 |
0,22 |
,В
,В
2) На частоте: f=0,4 кГц, при =0,7:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,88 |
0 |
1 |
2,76 |
3,22 |
3,17 |
3,08 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,88 |
-3 |
-2 |
-0,24 |
0,22 |
0,17 |
0,08 |
0,05 |
0,05 |
0,05 |
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,91 |
-0,32 |
0,63 |
2 |
2,65 |
2,91 |
3 |
3,04 |
3,05 |
3 |
ΔU,В |
-3,91 |
-3,32 |
-2,37 |
-1 |
-0,35 |
-0,09 |
0 |
0,04 |
0,05 |
0 |
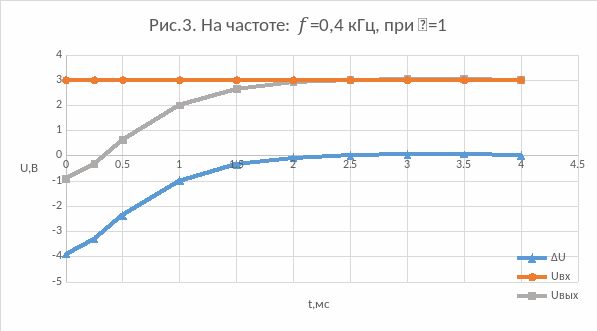
3) На частоте: f=0,4 кГц, при =1:
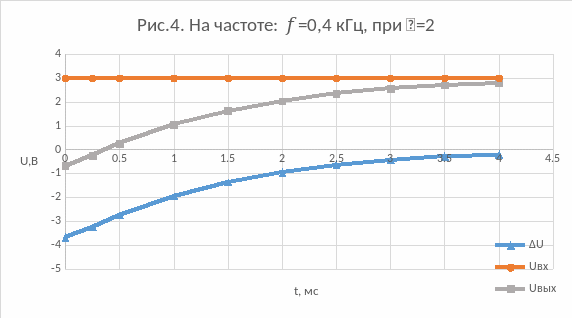
4) На частоте: f=0,4 кГц, при =2:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,68 |
-0,25 |
0,26 |
1,05 |
1,63 |
2,04 |
2,36 |
2,56 |
2,71 |
2,79 |
ΔU,В |
-3,68 |
-3,25 |
-2,74 |
-1,95 |
-1,37 |
-0,96 |
-0,64 |
-0,44 |
-0,29 |
-0,21 |
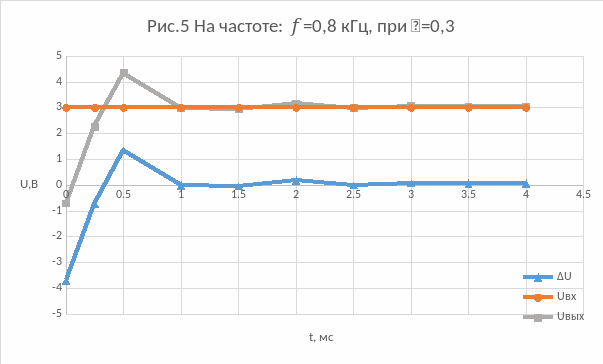
5) На частоте: f=0,8 кГц, при =0,3:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,71 |
2,26 |
4,35 |
2,98 |
2,95 |
3,17 |
2,99 |
3,07 |
3,05 |
3,05 |
ΔU,В |
-3,71 |
-0,74 |
1,35 |
-0,02 |
-0,05 |
0,17 |
-0,01 |
0,07 |
0,05 |
0,05 |
6) На частоте: f=0,8 кГц, при =0,7:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,69 |
1,07 |
2,8 |
3,16 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,69 |
-1,93 |
-0,2 |
0,16 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
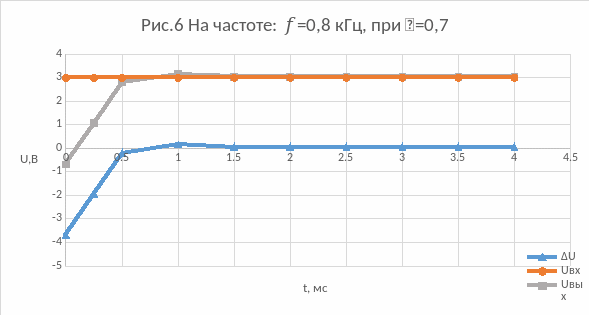
7) На частоте: f=0,8 кГц, при =1:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,78 |
0,84 |
2,07 |
2,92 |
3,03 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,78 |
-2,16 |
-0,93 |
-0,08 |
0,03 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
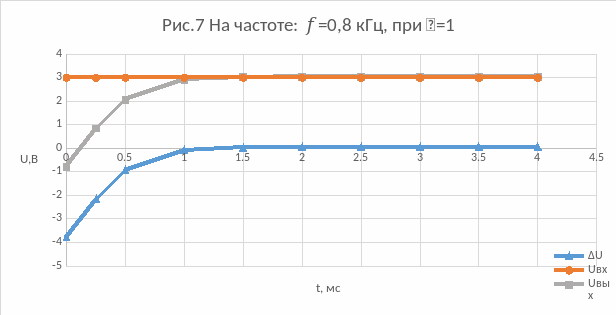
8) На частоте: f=0,8 кГц, при =2:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,79 |
0,23 |
1,06 |
2,03 |
2,5 |
2,8 |
2,92 |
2,99 |
3,02 |
3,04 |
ΔU,В |
-3,79 |
-2,77 |
-1,94 |
-0,97 |
-0,5 |
-0,2 |
-0,08 |
-0,01 |
0,02 |
0,04 |
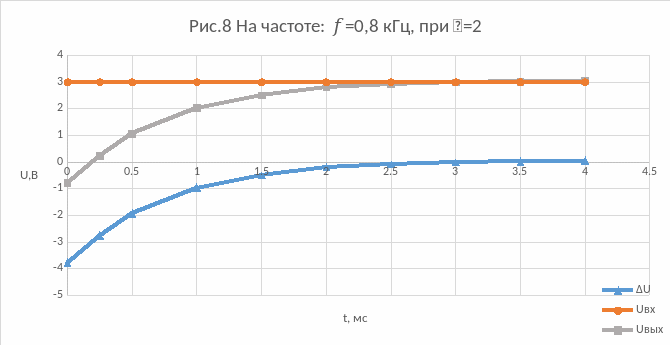
9) На частоте: f=1,2 кГц, при =0,3:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,52 |
3,82 |
3,9 |
2,88 |
3,02 |
3,07 |
3,04 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,52 |
0,82 |
0,9 |
-0,12 |
0,02 |
0,07 |
0,04 |
0,05 |
0,05 |
0,05 |
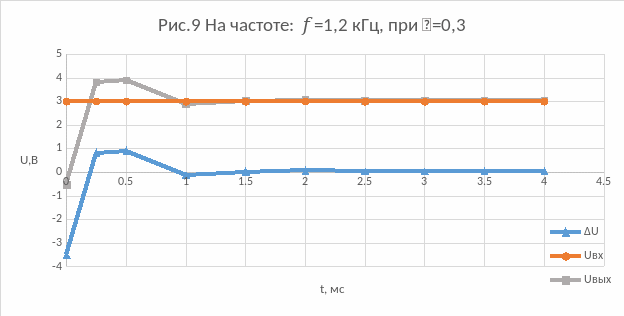
10) На частоте: f=1,2 кГц, при =0,7:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,55 |
2,45 |
3,19 |
3,04 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,55 |
-0,55 |
0,19 |
0,04 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,44 |
2,36 |
2,94 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,44 |
-0,64 |
-0,06 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
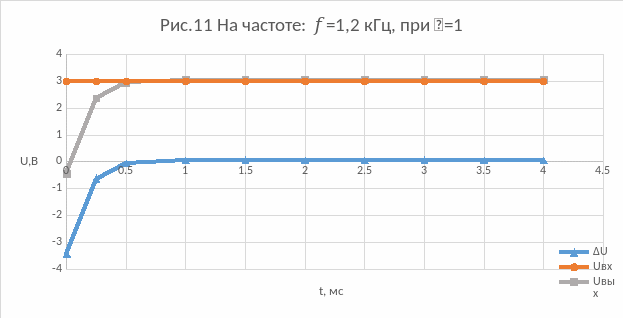
11) На частоте: f=1,2 кГц, при =1:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,42 |
2,34 |
2,95 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,42 |
-0,66 |
-0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
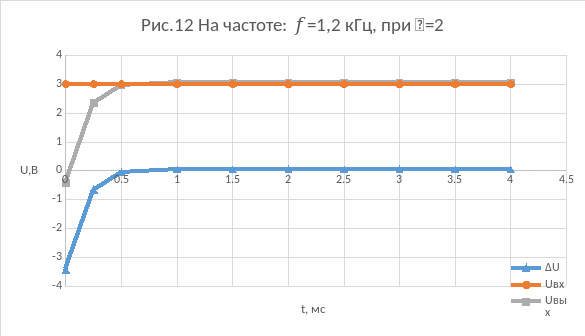
12) На частоте: f=1,2 кГц, при =2:
t,i |
0 |
0,25 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
,В |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
,В |
-0,25 |
4,47 |
2,73 |
3,1 |
3,07 |
3,05 |
3,05 |
3,05 |
3,05 |
3,05 |
ΔU,В |
-3,25 |
1,47 |
-0,27 |
0,1 |
0,07 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |