Лабораторно-практическая работа № 1 - Построение минимальных путей в ориентированной сети методом Дейкстра

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Петербургский государственный университет путей сообщения

Императора Александра I»

Кафедра «Высшая математика»

Лабораторно-практическая работа № 1

по дисциплине «Математическое моделирование

систем и процессов»

Построение минимальных путей в ориентированной сети методом Дейкстра

Вариант 20

Выполнил: Васечкин А. А.

факультета ТЭС

группы ПТМ-014

****************.

Проверил: профессор

Боровских Ю.В.

Санкт-Петербург

2023

Задание:

Изобразить в виде рисунков ориентированную сеть , заданную весовой матрицей 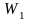. Построить для сети кратчайший путь от узла до x₆ c помощью алгоритма Дейкстры.

Исходные данные:

W₁=

Решение:

1. Построение графа

X6

X5

7

X1

5 9 6

4

X4

10

4

5

3

4

X3

X2

6

Этап 1 (Нахождение длины кратчайшего пути)

Шаг 0 (Расстановка начальных меток)

d(s) = d(x1) = 0*

d(x2) = d(x3) = d(x4) = d(x5) = d(t) =

+∞

7 +∞

5 6

9 4

10 +∞

0*

4

3

5

4

+∞ 6 +∞

Шаг 1 (Изменение меток)

u = s

Г+(u) = {x2, x3, x4}

d.new(x2) = min{d.old(x2), d(u) + w(u, x2)} = min{ , 4} = 4

d.new(x3) = min{d.old(x3), d(u) + w(u, x3)} = min{ , 5} = 5

d.new(x4) = min{d.old(x4), d(u) + w(u, x4)} = min{ , 10} = 10

Шаг 2 (Превращение метки в постоянную)

d(x)*=min{d(y),yꞓX,d(y) – временная}

min{d(x2), d(x3), d(x4), d(x5), d(t)} = min{4, 5, 10, , } = 4

Шаг 3:

u ≠ t, переходим к шагу 1

+∞

7 13

6

5 9

4

10 8

0 4

3

4

5

6 5

4

Шаг 1:

u = x2

Г+(u) = {x3, x4, x5}

d.new(x3) = min{d.old(x3), d(u) + w(u, x3)} = min{5, 11} = 5

d.new(x4) = min{d.old(x4), d(u) + w(u, x4)} = min{10, 8} = 8

d.new(x5) = min{d.old(x5), d(u) + w(u, x5)} = min{ , 13} = 13

Шаг 2:

min{d(x3), d(x4), d(x5); d(t)} = min{5, 8, 13, )= 5

Шаг 3:

u ≠ t, переходим к шагу 1

10

7 13

6

5 9

4

10 8

0 4

3

4

5

6 5

4

Шаг 1:

u = x3

Г+(u) = {x4, x5, x6}

d.new(x4) = min{d.old(x4), d(u) + w(u, x4)} = min{8, 8} = 8

d.new(x5) = min{d.old(x5), d(u) + w(u, x5)} = min{13, 9} = 9

d.new(x6) = min{d.old(x6), d(u) + w(u, x6)} = min{ , 10} = 10

Шаг 2:

min{d(x4), d(x5); d(x6)} = min{8, 9, 10}=8

Шаг 3:

u ≠ t, переходим к шагу 1

10

7 13

6

5 9

4

10 8

0 4

3

4

5

6 5

4

Шаг 1:

u = x4

Г+(u) = {x5}

d.new(x5) = min{d.old(x5), d(u) + w(u, x5)} = min{13, 14} = 13

Шаг 2:

min{d(x5)} = min{13}=13

Шаг 3:

u ≠ t, переходим к шагу 1

10

7 13

6

5 9

4

10 8

0 4

3

4

5

6 5

4

Шаг 1:

u = x5

Г+(u) = {x6}

d.new(x6) = min{d.old(x6), d(u) + w(u, x6)} = min{10, 20} = 10

Шаг 2:

min{d(x6)} = min{10}=10

Шаг 3:

u ≠ t, переходим к шагу 1

10

7 13

6

5 9

4

10 8

0 4

3

4

5

6 5

4

Этап II «Определение минимального пути методом последовательного возвращения»

Шаг 1:

u = t

Г-(u) = {x3, x5}

d(u) = d(xi) + w(xi, u); i = 3, 5

x3: 5 + 5 = 10 = 10

x5: 13 + 7 = 20 ≠ 10

Выбираем для минимального пути дугу (x3, t)

Шаг 2:

X3 ≠ s, переходим к шагу 1

Шаг 1:

u = x3

Г-(u) = {x1, x2}

d(u) = d(xi) + w(xi, u); i = 1, 2, 3

x1: 0 + 5 = 5 = 5

x2: 4 + 6 = 10 ≠ 5

Выбираем для минимального пути дугу (s, x3)

Шаг 2:

s = s, этап II завершен

Ответ: минимальным путем из s в t является путь s – x3 – t

цена пути = 10