
Лабораторная работа (Вариант 20) - Компьютерное моделирование основных процессов и статистическая оценка характеристик СМО
.docxПетербургский Государственный Университет Путей Сообщения
Лабораторная работа: Компьютерное моделирование основных процессов и статистическая оценка характеристик СМО
Вариант – 20
Выполнил:
Васечкин А.А. ПТМ-014
Проверил:
Санкт-Петербург
2023 г.
Цель работы: Моделирование работы открытой и замкнутой СМО M|M|m|n с параметрами:
λ= 1.25; µ = 0.1; m=3; n=0;
λ= 23.8; µ = 19.2; m=1; n=inf; S=6
Построение получившейся траектории процесса Q(t) и оценка основных характеристик смоделированной системы.
Теоретическая часть
Открытые СМО
Система M|M|m|n имеет m одинаковых параллельно работающих приборов и n мест для ожидания. Входящий поток требований простейший с интенсивностью λ, время обслуживания – показательное с параметром µ. Максимальное число требований, которые могут находиться в системе, равно m + n. Любое поступившее сверх этого числа требование получает отказ и покидает систему без обслуживания. Число требований Q(t), находящихся в системе в момент времени t, является марковским процессом рождения и гибели с множеством состояний {0, 1, . . . , m + n} .

Замкнутые СМО

Код программы для решения задачи
Моделирование открытой СМО
Система M|M|n|m, с параметрами λ= 1.25; µ = 0.1; m=3; n=0
lambda=1.25; mu=0.1;
m=3; n=0;
N=m+n+1;% число возможных состоний системы
% Определение вспомогательных переменных
Num=50;
s=1;% индекс текущего состони системы
T=zeros(1,Num);% вектор моментов изменений состоний
Qt=zeros(1,Num);% состони процесса Q(t) в моменты изменений
% состоний системы
Time=zeros(1,N);% вектор, в котором накапливаютс суммарные
% времена пребывани системы в состоних 0, 1, . . . , m + n
for i=2:Num,
switch Qt(i-1)
case 0
v=Inf;u=-log(rand)/lambda;
case m+n
u=Inf;v=-log(rand)/(m*mu);
otherwise
u=-log(rand)/lambda;
qs=min(m,Qt(i-1));% число работающих приборов
v=-log(rand)/(qs*mu);
end;
delta_time=min(u,v);
T(i)=T(i-1)+delta_time;
Time(s)=Time(s)+delta_time;
if u<v
Qt(i)=Qt(i-1)+1;
else
Qt(i)=Qt(i-1)-1;
end;
s=Qt(i)+1;% индекс текущего состони
end;
z=zeros(1,Num);
mvect=ones(1,Num)*m;
qt=max(z,Qt-mvect);
subplot(211);plot(T,Qt);
subplot(212);plot(T,qt);
disp('Оценки характеристик системы M|M|5|8,');
disp('пролученные на основе моделировани');
Psost=Time/T(Num);
disp('Веротность просто'); disp(Psost(1));
disp('Веротности состоний 1,...,m+n'); disp(Psost(2:N));
disp('Веротность ожидани'); Pw=1-sum(Psost(1:m)); disp(Pw);
disp('Веротность отказа'); PL=Psost(N); disp(PL);
disp('Среднее число завок в системе');
k=0:(N-1); Qsr=k*Psost'; disp(Qsr);
disp('Среднее число завок в очереди');
z=zeros(1,N); qsr=max(z,k-m)*Psost'; disp(qsr);

Числовые характеристики открытой СМО:
lambda=1.25; mu=0.1;
m=3; n=0;
rho=lambda/mu; rho_m=rho/m;
N=m+n;
% Вычисление веротностей p0, p1, . . . , p12
x=1:N;
x1=ones(1,N)*m;
xx=min(x,x1);% вектор длины N, равный (1, 2, . . . , m, . . . , m)
slave1=ones(1,N)*rho;
slave2=slave1./xx;% вектор длины N,
slave=cumprod(slave2);% вектор (ρ,
disp('Веротность просто системы');
P0=1/(1+sum(slave)); disp(P0);
disp('Веротности состоний 1,...,N');
Psost=slave*P0; disp(Psost);
disp('Веротность потери требовани');
Potk=Psost(N); disp(Potk);
disp('Веротность ожидани перед обслуживанием');
Pw=sum(Psost(m:N-1)); disp(Pw);
disp('Веротность обслуживани без ожидани');
Pww=1-Psost(m)*(1-rho_m^(n+1))/(1-rho_m); disp(Pww);
disp('Среднее число завок в системе');
Qsr=(1:N)*Psost'; disp(Qsr);
xx1=x-x1;
disp('Среднее число завок в очереди');
qsr=Psost(m)*rho_m/(1-rho_m)^2; disp(qsr);
disp('Среднее число зантых приборов');
qs=xx*Psost'; disp(qs);
disp('Среднее врем ожидани');
W=m*Psost(m)/mu/(m-rho)^2*(1-(n+1)*rho_m^n+n*rho_m^(n+1));
disp(W);
disp('Среднее врем пребывани в системе');
T=W+1/mu; disp(T);
% График функции распределени времени ожидани FW (t)
t=0:0.01:10;
slv1=[];slv2=[];
if n>1
for k=1:n-1
slv1=[slv1;(m*mu*rho_m*t).^k./prod(1:k)];
slv2=[slv2;(m*mu*t).^k./prod(1:k)];
end;
slv1=sum(slv1);slv2=sum(slv2);
% Вычисление Pn−1
slv=slv1-slv2*rho_m^n+1-rho_m^n;
else
slv=1-rho_m^n;
end;
FW=1-Psost(m)/(1-rho_m)*exp(-m*mu*t).*slv;
plot(t,FW);

Моделирование замкнутой СМО
Система M|M|m|n|S: λ= 23.8; µ = 19.2; m=1; n=inf; S=6
lambda=23.8; mu=19.2; m=1;
Num=50;
s=6;
T=zeros(1,Num);
Qt=zeros(1,Num);
Time=zeros(1,Num);
for i=2:Num,
if Qt(i-1)==0
v=Inf;u=-log(rand)/lambda;
else
u=-log(rand)/lambda;
qs=min(m,Qt(i-1));
v=-log(rand)/(qs*mu);
end;
delta_time=min(u,v);
T(i)=T(i-1)+delta_time;
Time(s)=Time(s)+delta_time;
if u<v
Qt(i)=Qt(i-1)+1;
else
Qt(i)=Qt(i-1)-1;
end;
s=Qt(i)+1;
end;
z=zeros(1,Num);
mvect=ones(1,Num)*m;
qt=max(0,Qt-mvect);
subplot(211);plot(T,Qt);
subplot(212);plot(T,qt);
disp ('Оценки характеристик системы M|M|1 с ожиданием,');
disp ('пролученные на основе моделировани');
Psost=Time/T(Num);
disp ('Веротность просто'); disp(Psost(1));
N=10; % ('Количество веротностей, которые необходимо вывести на экран');
disp ('Веротности состоний 1,...,N'); disp(Psost(2:N+1));
disp ('Веротность ожидани'); Pw=1-sum(Psost(1:m)); disp(Pw);
disp ('Среднее число завок в системе');
k=0:(Num-1); Qsr=k*Psost'; disp(Qsr);
disp ('Среднее число завок в очереди');
qsr=max(0,k-m)*Psost'; disp(qsr);

Числовые характеристики закрытой СМО:
lambda=23.8; mu=19.2;
m=1; n=8; S=6;
rho=lambda/mu;
M=min(m+n,S);
% Вычисление веротностей
x=1:M;
x1=ones(1,M-m)*m;
x2=S-x+1;
xx=[x(1:m),x1];xx1=xx./x2;
slave1=ones(1,M)*rho;
slave2=slave1./xx1;
slave=cumprod(slave2);
disp('Веротность просто');
P0=1/(1+sum(slave)); disp(P0);
disp('Веротности состоний 1,...,M');
Psost=slave*P0; disp(Psost);
disp('Веротность потери требовани');
PL=Psost(M); disp(PL);
disp('Веротность ожидани перед обслуживанием');
Pw=sum(Psost(m:M-1)); disp(Pw);
disp('Веротность обслуживани без ожидани');
Pww=P0+sum(Psost(1:m-1)); disp(Pww);
disp('Среднее число завок в системе');
Qsr=x*Psost'; disp(Qsr);
xq=x-xx;
disp('Среднее число завок в очереди');
qsr=xq((m+1):M)*(Psost((m+1):M))'; disp(qsr);
disp('Среднее число зантых приборов');
qs=xx*Psost'; disp(qs);
disp('Среднее врем ожидани');
W=((1:n)/m/mu) * (Psost(m+1):M)'; disp(W);
disp('Среднее врем пребывани в системе');
T=W+1/mu; disp(T);
% График функции распределени времени ожидани FW (t)
t=0:0.01:10;
FW=1-Pw*exp(-(m*mu-lambda)*t);
plot(t,FW);

Результаты работы программы
Моделирование открытой СМО

Число изменений состояния системы за время моделирования 50
Оценки характеристик системы М|M|3|0, полученные на основе моделирования:
Вероятность простоя - 0.0094;
Количество вероятностей, которые необходимо вывести на экран 3
Вероятности состояний 1,...3:
0.0142 0.2207 0.7557;
Вероятность ожидания- 0.7557;
Вероятность отказа – 0.7557;
Среднее число заявок в системе - 2.7226;
Среднее число заявок в очереди - 0;
Числовые характеристики открытой СМО
Вероятность простоя системы – 0.0024;
Вероятность состояний 1…,3:
0.300 0.1873 0.7804
Вероятность отказа- 0.7804;
Вероятность обслуживания с ожиданием- 0;
Вероятность обслуживания без ожидания- 0.2196;
Среднее число заявок в системе- 2.7456;
Среднее число заявок в очереди- 0.3242;

Можно заметить отличие в характеристиках СМО при моделировании и расчётах. Чтобы уменьшить расхождение в значениях, увеличим Число изменений состояния системы за время моделирования до 500000.
Таким образом получаем характеристики системы:
Вероятность простоя - 0.0023;
Количество вероятностей, которые необходимо вывести на экран 3
Вероятности состояний 1,..., 3:
0.0300 0.1872 0.7805;
Вероятность ожидания- 0.7805;
Вероятность отказа – 0.7805;
Среднее число заявок в системе - 2.7460
Среднее число заявок в очереди - 0;
Что уже более приближенно к расчётным значениям.
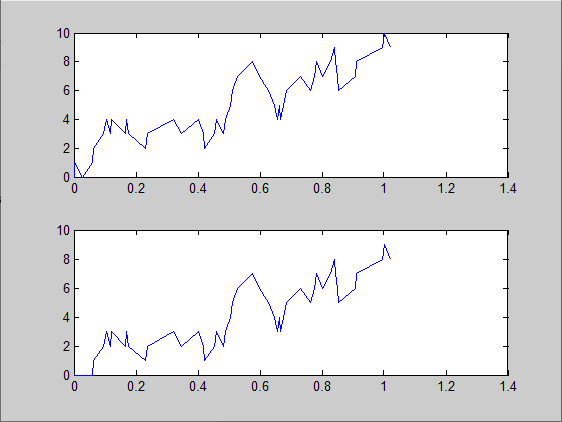
Моделирование замкнутой СМО
Число изменений состояния системы за время моделирования 50
Оценки характеристик системы M|M|1|inf|6, полученные на основе моделирования:
Вероятность простоя системы - 0.0297;
Вероятность ожидания – 0.9703;
Вероятность состояний 1…N:
0.0302 0.0721 0.2196 0.1568 0.031 0.1433 0.1506 0.1408 0.0069 0.0211;
Среднее число заявок в системе - 4.9202;
Cреднее число заявок в очереди- 3.9499;
Числовые характеристики замкнутой СМО:
Вероятность простоя- 0.00017087
Вероятности состояний:
0.0013 0.0079 0.0391 0.1452 0.3601 0.4463;
Вероятность потери требования- 0.4463
Вероятность ожидания перед обслуживанием- 0.5535
Вероятность обслуживания без ожидания- 0.00017087
Среднее число заявок в системе- 5.1934
Среднее число заявок в очереди-4.1936
Среднее число занятых приборов- 0.9998
Вывод
В данной лабораторной работе было проведено моделирование работы
1. открытой СМО с параметрами λ= 1.25; µ = 0.1; m=3; n=0;
2. замкнутой СМО с параметрами λ= 23.8; µ = 19.2; m=1; n=inf; S=6
Построена траектория процесса Q(t) и дана оценка основных характеристик смоделированной системы и оценка числовых характеристик.
