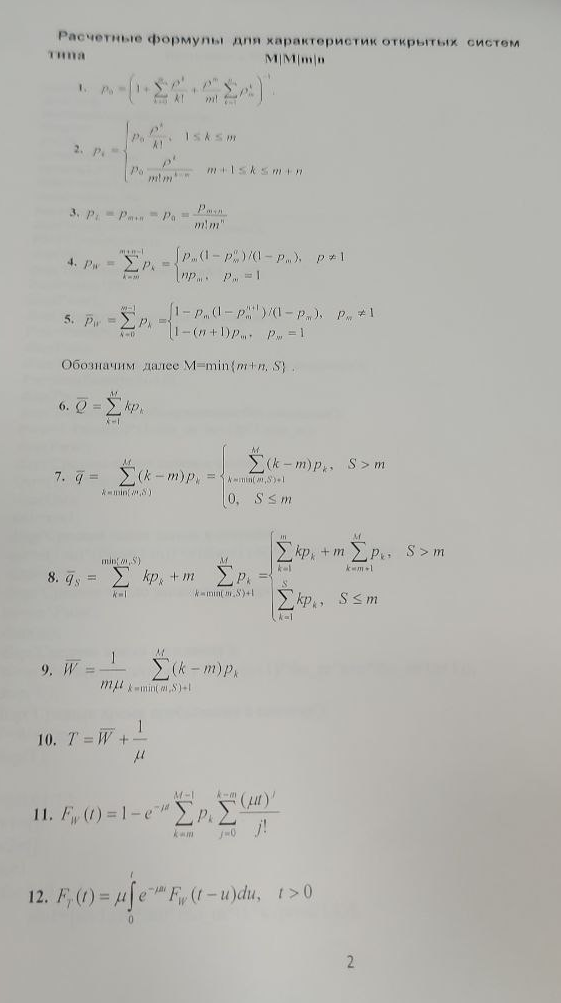Ответы к практическому вопросу

1. Дейкстра (минимальный путь)

Решение:

1. Построение графа

Этап 1 (Нахождение длины кратчайшего пути)

Шаг 0 (Расстановка начальных меток)

d(s) = d(x1) = 0*

d(x2) = d(x3) = d(x4) = d(x5) = d(t) =

Шаг 1 (Изменение меток)

u = s

Г+(u) = {x2, x3, x4}

d.new(x2) = min{d.old(x2), d(u) + w(u, x2)} = min{ , 4} = 4

d.new(x3) = min{d.old(x3), d(u) + w(u, x3)} = min{ , 5} = 5

d.new(x4) = min{d.old(x4), d(u) + w(u, x4)} = min{ , 10} = 10

Шаг 2 (Превращение метки в постоянную)

d(x)*=min{d(y),yꞓX,d(y) – временная}

min{d(x2), d(x3), d(x4), d(x5), d(t)} = min{4, 5, 10, , } = 4

Шаг 3:

u ≠ t, переходим к шагу 1

и так далее

Этап II «Определение минимального пути методом

последовательного возвращения»

Шаг 1:

u = t

Г-(u) = {x3, x5}

d(u) = d(xi) + w(xi, u); i = 3, 5

x3: 5 + 5 = 10 = 10

x5: 13 + 7 = 20 ≠ 10

Выбираем для минимального пути дугу (x3, t)

Шаг 2:

X3 ≠ s, переходим к шагу 1

и так далее

2. Максимальный путь

Решение:

1. Построение графа

Этап 1 (Нахождение цены максимального пути)

Шаг 0 (Расстановка начальных меток)

d(s) = d (x1) = 0

d (x2) = max{d(s)+4}=max{4}=4

d (x3) = max{d(s)+5}=max{5}=5

d (x3) = max{d(s)+4, d(x2)+6}=max{10}=10

d (x4) = max{d(s)+10}=max{10}=10

d (x4) = max{d(s)+4, d(x2)+4}=max{8}=8

d (x4) = max{d(s)+4, d(x2)+6, d(x3)+3}=max{13}=13

d (x5) = max{d(s)+4, d(x2)+6, d(x3)+3, d(x4)+6}=max{19}=19

d (x6) = max{d(s)+4, d(x2)+6, d(x3)+3, d(x4)+6, d(x5)+7}=max{26}=26

Максимальная цена пути из вершины s в t равна 26, переходим к этапу II

Этап II «Определение максимального пути методом последовательного возвращения»

Шаг 1: (1-я итерация)

u = t

Г-(u) = {x4, x5}

d(u) = d(xi) + w(xi, u); i = 4, 5

x3: 10 + 5 = 15 ≠ 26

x5: 19 + 7 = 26 = 26

Выбираем для максимального пути дугу (x5, t)

Шаг 2:

x5 ≠ s, переходим к шагу 1

и так далее

3. Беллман-Форд (минимальный путь)

Решение:

1. Построение графа

Этап 1 Q(k) – множество вершин понизивших свои метки на шаге k (л=0, 1, 2)

P(k) – множество вершин, следующих за вершинами, которые понизили свои метки.

P(k)=Г+(Q(k))

Шаг 0

l(s) = 0; l(xi) = ∞

Q(0) = {s}; P(0) = {x2, x3, x5} = Г+(Q(0))

Шаг 1.1

l(x2) = min {∞, 6} = 6

l(x3) = min {∞, 8} = 8

l(x5) = min {∞, 12} = 12

Шаг 2.1

Q(1) = {x2, x3, x5}; P(1) = {x3, x4, x4, x5, x4, x6}

и так далее

Этап 2

Шаг 1.1

u=x6; Г-(u) = {x4, x5}

x4: 2+5 = 7 = 7

x5: 5+6 = 11 ≠ 7

x4 ≠ s

Шаг 1.2

u=x4; Г-(u) = {x2, x3, x5}

x2: 6+9 = 15 ≠ 2

x3: 1+7 = 8 ≠ 2

x5: 5-3 = 2 = 2

x5 ≠ s

и так далее

Ответ: минимальный путь s – x2 – x3 – x5 – x4 - t; цена пути:

4. Алгоритм Краскала (минимальный остов)

Решение:

Построение графа

1. [v2, v3], [v3, v6], [v1, v2], [v6, v4], [v3, v4], [v1, v4], [v1, v5], [v5, v6],

[v4, v6]

2. C1 = {v1}

C2 = {v2}

C3 = {v3}

C4 = {v4}

C5 = {v5}

C6 = {v6}

3. E׳= пустое множество

4. 1 итерация

e = [v2, v3]

C2 := C2 u C3 = {v2, v3}

E’ = E’ u {e} = {[v2, v3]}

2 итерация

e = [v3, v6]

E’ = E’ u {e} = {[v2, v3], [v3, v6]}

C2 = C2 u C6 = {v2, v3, v6}

3 итерация

e = [v1, v2]

E’ = E’ u {e} = {[v2, v3], [v3, v6], [v1, v2]}

C2 = C2 u C1 = {v1, v2, v3, v6}

и так далее

9 итерация

e = [v4, v6]

завершена! v4, v6 Є C2

#E’ = 5

n = 6

#E’ = n-1 = 5 Ответ: цена минимального пути 33

5. Алгоритм Прима (минимальный остов)

Решение:

1. Построение графа

Шаг 0 – Берем любую вершину графа v ϵ V:

v2 ϵ V

V’ = {v2}

V’’ = V \ v2 = {v1, v3, v4, v5, v6}

E’ = Ø

Шаг 1 – Определяем в разрезе ребро с минимальным весом: (1-я итерация)

E(V’, V’’) = {[v2, v1], [v2, v3]}

e* = [v2, v3]

w(e*) = 3

Шаг 2 – Обновляем граф и подграф:

V’new = {v2, v3}

V’’new = {v1, v4, v5, v6}

E’new = {[v2, v3]}

Шаг 3 – проверка на завершение алгоритма:

#E’ ≠ 5, переходим к шагу 1

и так далее

Шаг 3:

#E’ = 5, алгоритм завершен

Ответ: цена минимального пути 33

6. Что-то там из 7 задачи